摩擦力

Friciton

干摩擦理论

Theory of Dry Friction / Coulomb Friction

干摩擦是一种存在于未润滑固体接触面之间、抵抗其相对滑动趋势或相对滑动的切向力；其大小在物体静止时与外力平衡，但在物体运动后则降为一个与法向力成正比的恒定值。

摩擦力的方向：摩擦力恒作用于接触面的切线方向，且其方向与物体即将发生或已经发生的运动方向相反。

This explanation based only on mechanical interactions is referred to as a classical approach. For a more complete analysis a detailed treatment of the nature of frictional forces must also include the effects of temperature, density, cleanliness, and atomic or molecular adhesion between the contacting surfaces, as well as the deformation and fracture at the points of contact. See, for example, M. Nosonovsky, Mechanical Engineering, March 2018.

静止状态

Impending Motion

$$\begin{array}{rl}{F}_s& ={\mu }_{s}N\\ {\varphi }_s& =\arctan (\frac{F_s}{N})=\arctan (\frac{{\mu }_{s}N}{N})=\arctan {\mu }_s\\ R_s& =N+F_s\end{array}$$

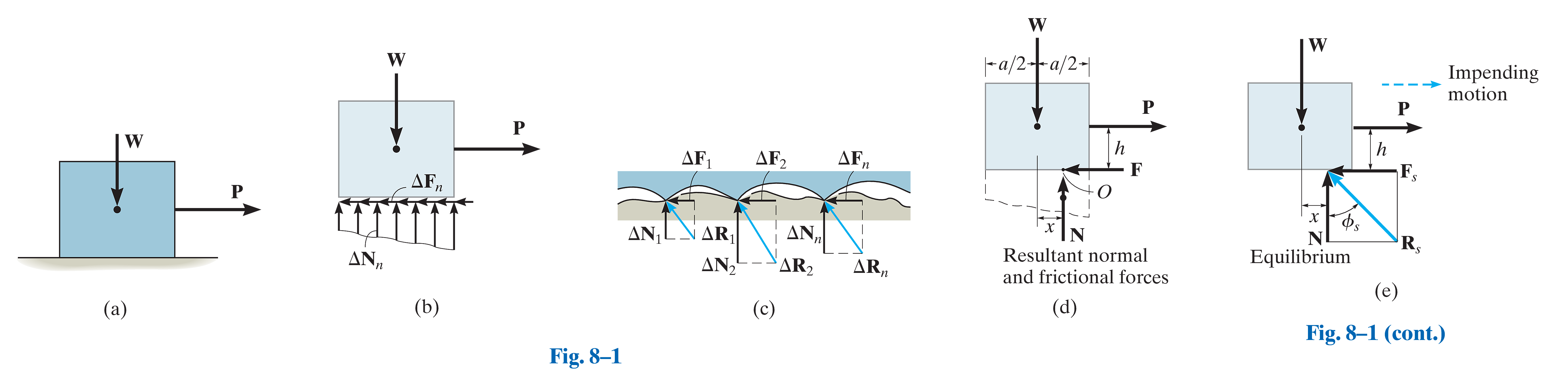
其中：

• $F_s$：静摩擦力 (static frictional force)
• ${\mu }_s$：静摩擦系数 (coefficient of static friction)

基于实验得来的经验数值。

• ${\varphi }_s$：静摩擦角 (angle of static friction)

$R_s$ 与 $N$ 的夹角为 ${\varphi }_s$。

• $R_s$：合力 (resultant force)

运动状态

Motion

$$\begin{array}{rl}{F}_k& ={\mu }_{k}N\\ {\varphi }_k& =\arctan (\frac{F_k}{N})=\arctan (\frac{{\mu }_{k}N}{N})=\arctan {\mu }_k\\ R_k& =N+F_k\end{array}$$

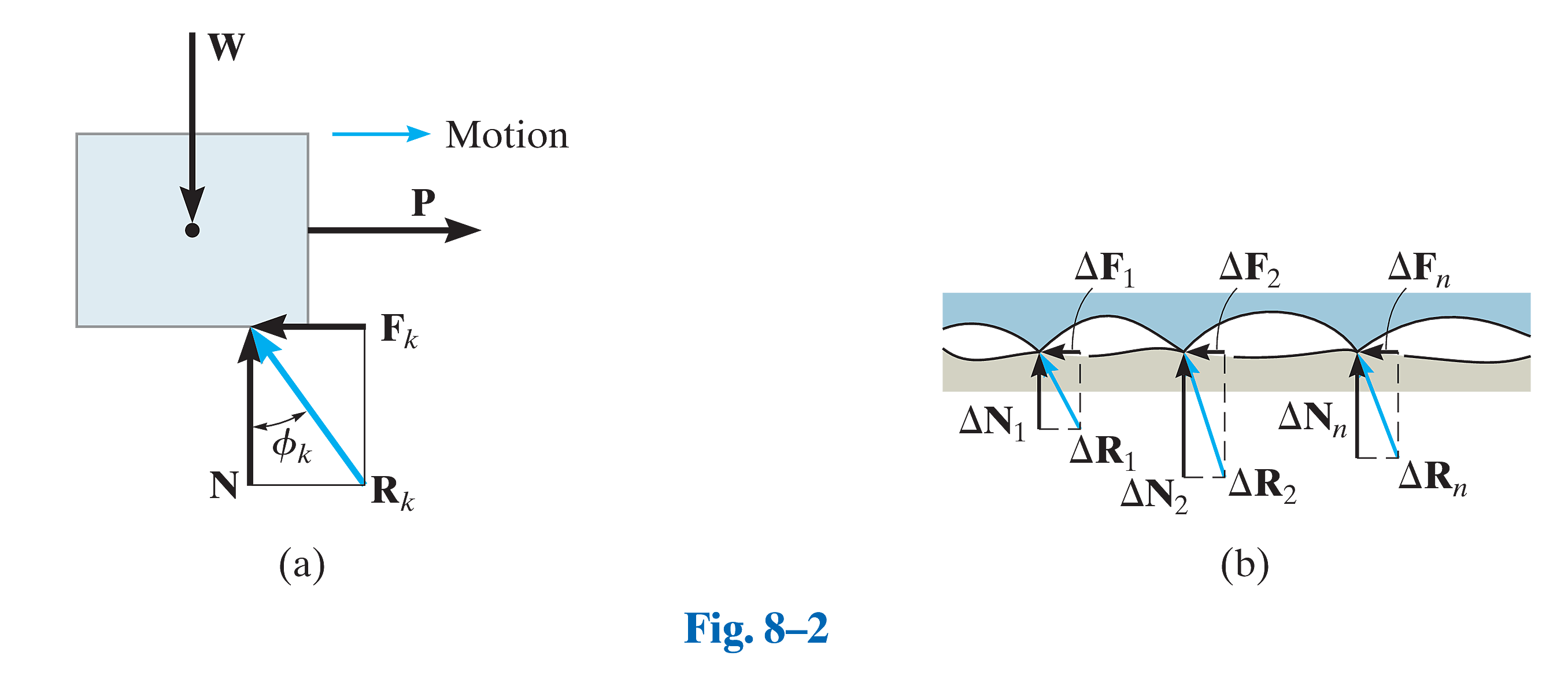
其中：

• $F_k$：动摩擦力 (kinetic frictional force)
• ${\mu }_k$：动摩擦系数 (coefficient of kinetic friction)

基于实验得来的经验数值。

• ${\varphi }_k$：动摩擦角 (angle of kinetic friction)

$R_k$ 与 $N$ 的夹角为 ${\varphi }_k$。

• $R_k$：合力 (resultant force)

摩擦效应

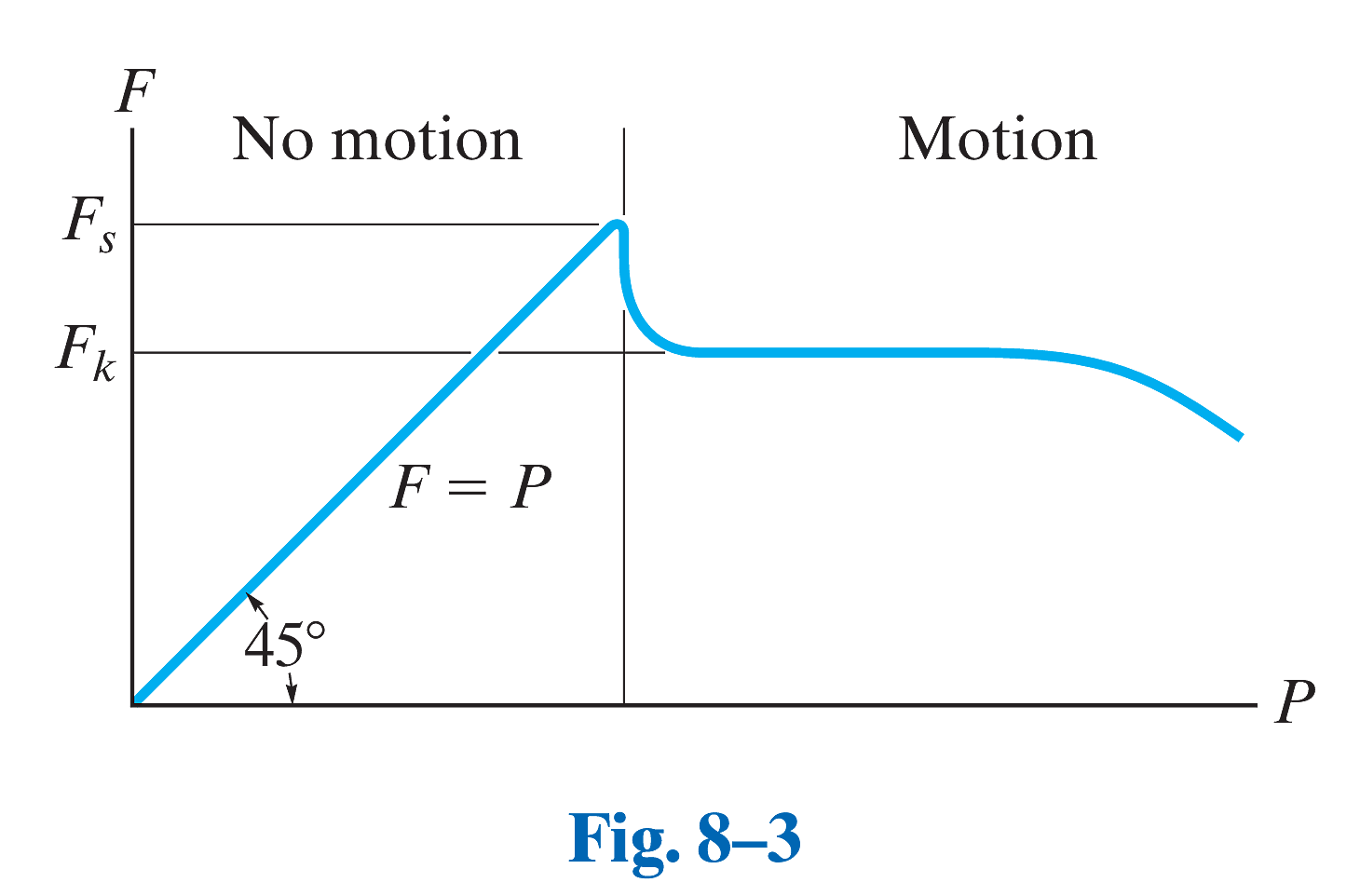
• F is a static frictional force if equilibrium is maintained.
• F is a limiting static frictional force Fs when it reaches a maximum value needed to maintain equilibrium.
• F is a kinetic frictional force Fk when sliding occurs at the contacting surface.

Notice also from the graph that for very large values of P or for high speeds, aerodynamic effects will cause $F_k$ and likewise ${\mu }_k$ to begin to decrease.

问题分类

• 没有明显的即将发生的运动 (No Apparent Impending Motion)
• 所有接触点均有即将发生的运动 (Impending Motion at All Points of Contact)
• 部分接触点有即将发生的运动 (Impending Motion at Some Points of Contact)

楔子

楔子是一种简单的机械 (machine)，通常用于将作用力转化为更大的力。楔子也可以用来稍微移动和调整重物。楔子一般用于分开、劈开或临时固定物体。

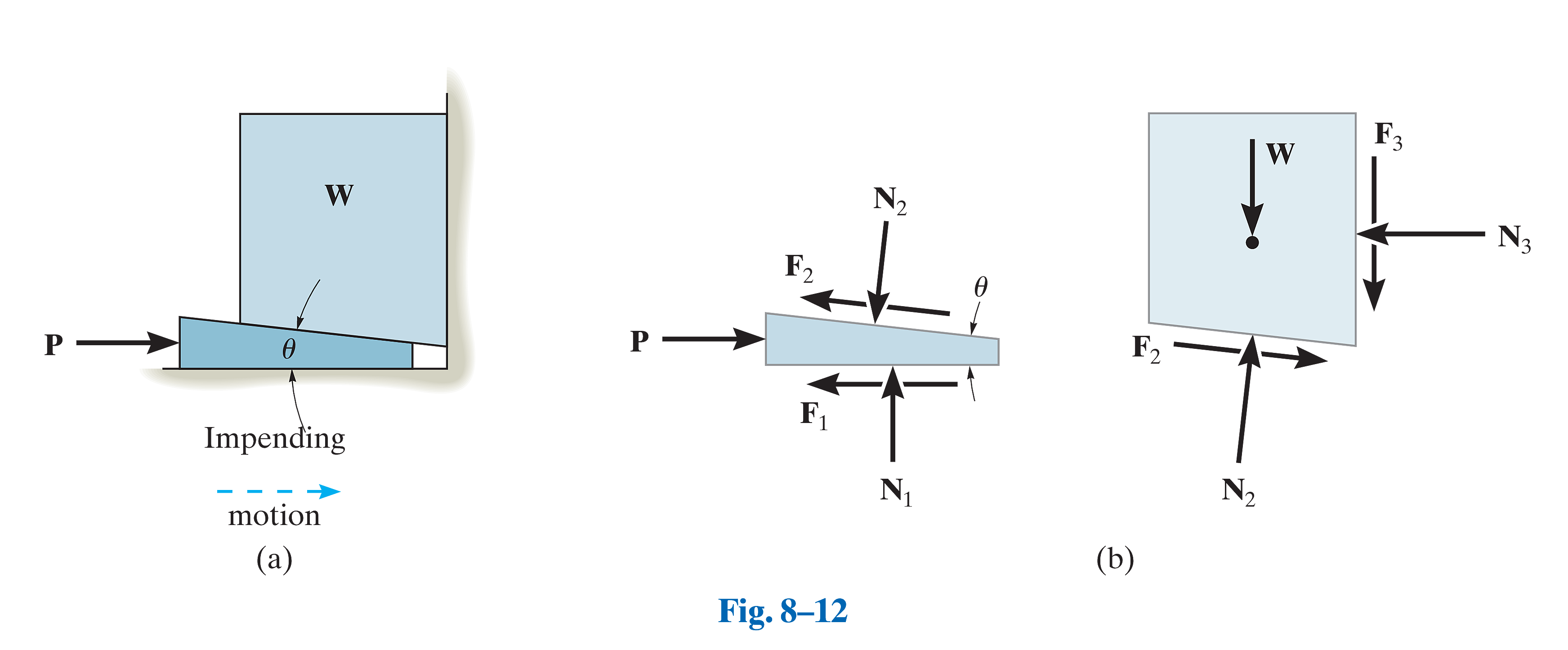
根据 Fig.8-12 的受力分析图，可以得到 7 个等式。其中前 4 个是平衡方程，后 3 个是摩擦力方程：

$$\{\begin{array}{rl}{F}_1-F_2\cos \theta -N_2\sin \theta & =-P\\ F_2\sin \theta +N_1-N_2\cos \theta & =0\\ F_2\cos \theta +N_2\sin \theta -N_3& =0\\ -F_3+N_2\cos \theta & =W\\ F_1-\mu N_1& =0\\ F_2-\mu N_2& =0\\ F_3-\mu N_3& =0\end{array}$$

矩阵乘法的形式为：

$$\left[\begin{array}{cccccc}-1& -\cos \theta & 0& 0& -\sin \theta & 0\\ 0& \sin \theta & 0& 1& -\cos \theta & 0\\ 0& \cos \theta & 0& 0& \sin \theta & -1\\ 0& 0& -1& 0& \cos \theta & 0\\ 1& 0& 0& -\mu & 0& 0\\ 0& 1& 0& 0& -\mu & 0\\ 0& 0& 1& 0& 0& -\mu \end{array}\right]\left[\begin{array}{c}{F}_1\\ F_2\\ F_3\\ N_1\\ N_2\\ N_3\end{array}\right]=\left[\begin{array}{c}-P\\ 0\\ 0\\ W\\ 0\\ 0\\ 0\end{array}\right]$$

螺纹

screw

矩形螺纹 single square-threaded screw

矩形螺纹

引言

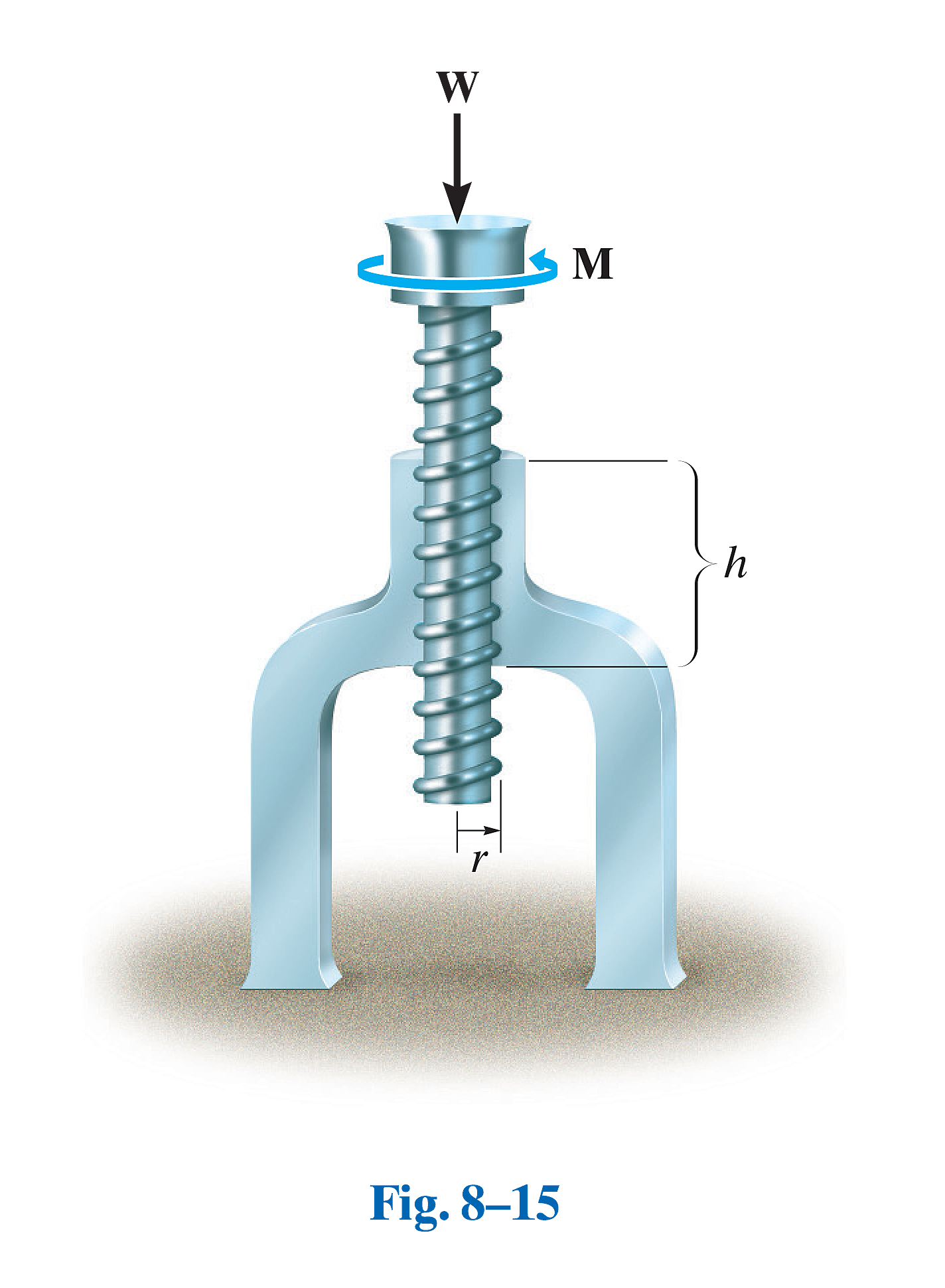
千斤顶和台虎钳这类机械装置，能够通过转动手柄（施加力矩 $M$）产生巨大的轴向力（载荷 $W$）。其核心机制便是矩形螺纹。直接对三维螺旋体进行力学分析相当复杂，因此，工程师们建立了一个巧妙的等效模型来简化问题：将三维螺纹展开，等效为一个二维的斜面滑块模型。

---

模型的建立与参数定义

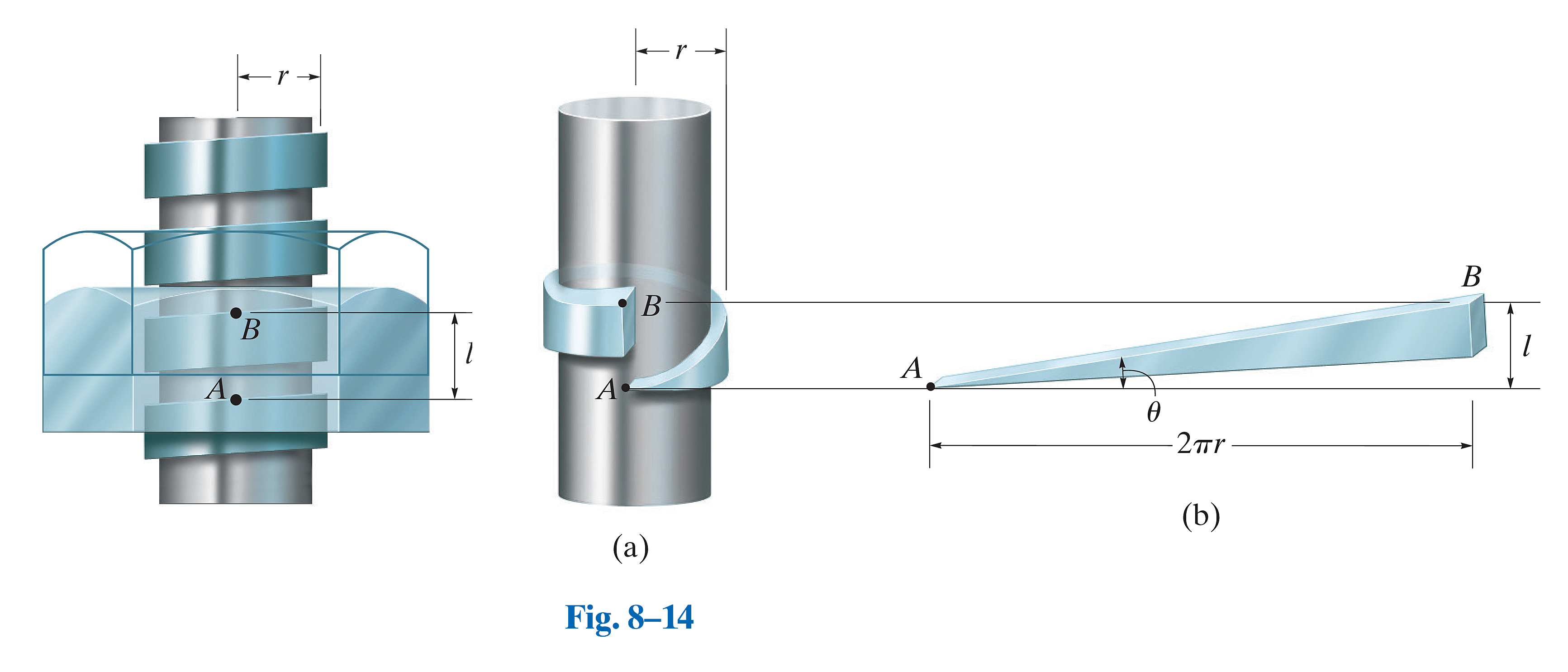
1. 核心思想：螺纹的展开

想象将螺杆上的一圈螺纹“剥下”并“展平”。这个过程会形成一个直角三角形，它就是我们分析所用的等效斜面。

• 斜面底边：等于螺纹一圈的周长，$2\pi r$。
• 斜面高度：等于螺杆旋转一圈后轴向移动的距离，即导程 $l$。

2. 关键几何参数

• 平均半径 (Mean Radius, $r$)：螺纹外径与内径的平均值，是计算力矩和周长的基准。
• 导程 (Lead, $l$)：螺杆或螺母旋转一整圈（360°）时，沿轴线方向移动的直线距离。
• 导程角 (Lead Angle, $\theta$)：等效斜面的倾角，它代表了螺纹的“陡峭”程度。其定义如下：$$\tan (\theta )=\frac{l}{2\pi r}$$

3. 力学等效与受力分析 (FBD)

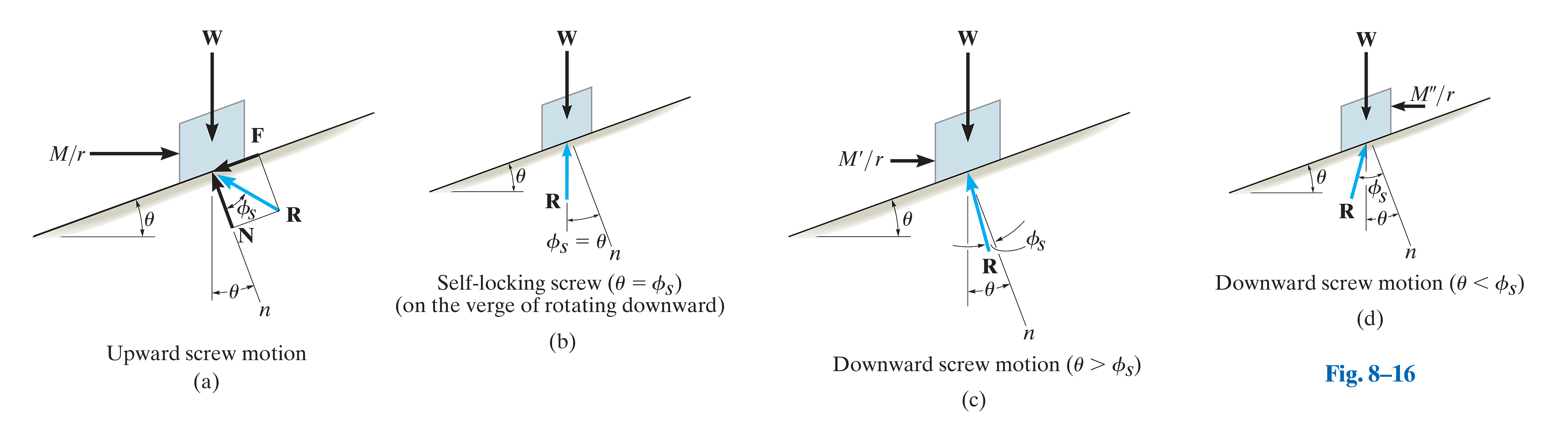
通过展开，我们将螺杆与螺母的相互作用，等效为滑块在斜面上的平衡问题。假设我们的目标是举起重物（或夹紧工件），滑块受力如下：

• 载荷 (Load, $W$)：等效为滑块的重力，方向垂直向下。
• 驱动力矩 (Moment, $M$)：等效为一个水平推力 $P$，推动滑块沿斜面向上运动。该力作用于平均半径 $r$ 处，满足关系 $M=P\cdot r$。
• 正向力 (Normal Force, $N$)：由斜面提供，方向垂直于斜面。
• 摩擦力 (Frictional Force, $F_s$)：方向与即将发生的运动趋势相反。由于要向上推动滑块，摩擦力方向为沿斜面向下。当处于临界平衡状态时，$F_s={\mu }_{s}N$。

4. 引入摩擦角 (${\varphi }_s$) 简化分析

为了进一步简化计算，我们引入静摩擦角 (Angle of Static Friction, ${\varphi }_s$) 的概念。

• 定义：静摩擦角 ${\varphi }_s$ 由静摩擦系数 ${\mu }_s$ 唯一确定，关系式为：$${\mu }_s=\tan ({\varphi }_s)\text{或}{\varphi }_s=\arctan ({\mu }_s)$$
• 作用：它巧妙地将正向力 $N$ 和摩擦力 $F_s$ 这两个力合并为一个合反力 $R$。这个合力 $R$ 与正向力 $N$ 之间的夹角，正好就是 ${\varphi }_s$。
• 优势：如此一来，原本作用在滑块上的四个力（$W,P,N,F_s$）就被简化为了三个力（$W,P,R$），使得后续的求解（如使用力三角形法）变得异常简洁。

---

总结

通过“展开螺纹”这一核心思想，我们将一个复杂的三维旋转动力问题，成功转化为一个经典、直观的二维静力学平衡问题。这个模型不仅清晰地揭示了力矩、载荷、螺纹几何和摩擦之间的内在关系，也为推导如 $M=rW\tan (\theta +{\varphi }_s)$ 这类关键计算公式奠定了坚实的理论基础。

平带

Flat Belts

核心概念与假设

1. 最大静摩擦力：分析的对象通常是“即将滑动” (Impending Motion) 的临界状态。在这种状态下，平带与接触面之间的静摩擦力达到了最大值。

2. 拉力传递：由于摩擦力的存在，皮带在接触面上缠绕时，一端的拉力可以远大于另一端。这也是为什么人们能用很小的力气，透过在杆子上绕几圈绳子，来拉住很重的物体。

3. 模型假设：

   • 平带是柔软且不可伸长的。

   • 平带的宽度相对于曲面的半径来说很小，因此可以被视为一条线。

   • 平带与曲面之间的摩擦力遵守库伦摩擦定律 ($F=\mu N$)。

   • 不考虑离心力，这个模型是针对“静力学”问题的。

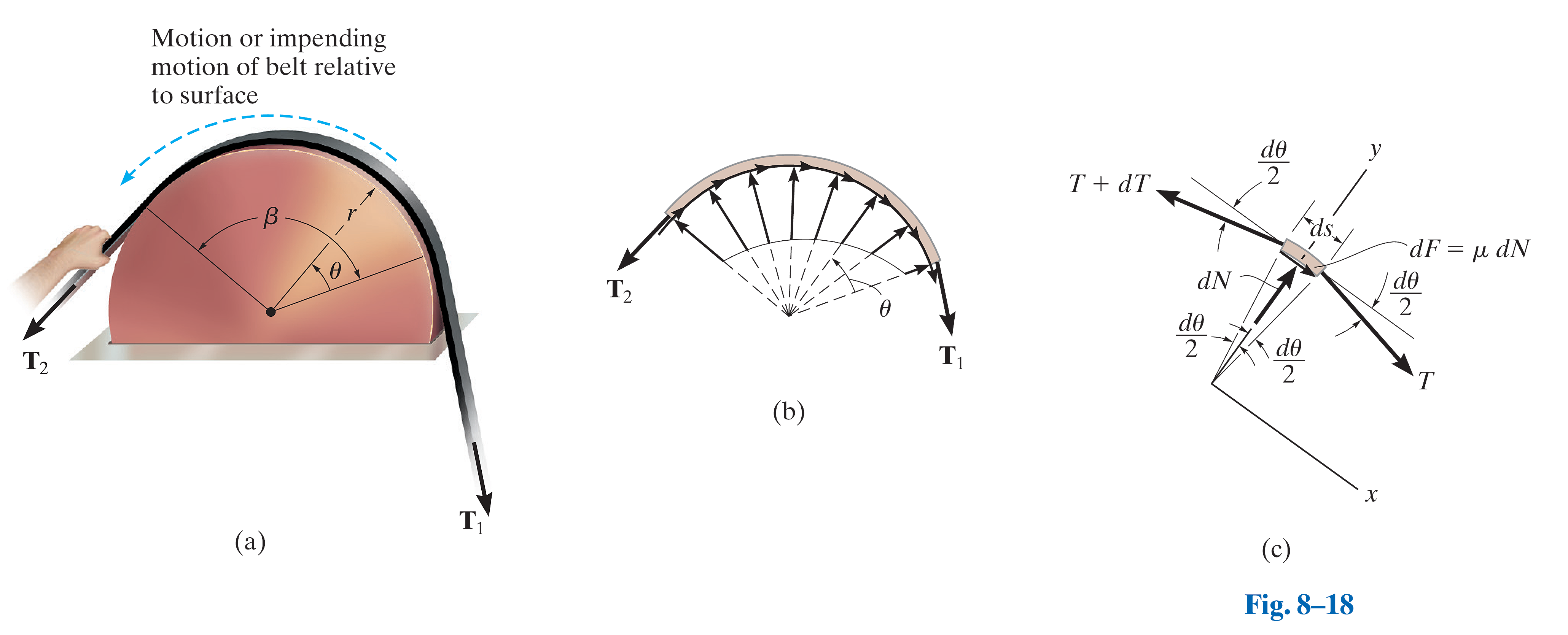
微元法受力分析

通常不直接分析整条平带这个复杂的对象，而是选取其中一个极其微小的部分（微元），这个微元的受力分析情况相对简单。透过分析这个微元的力平衡，可以找到一个描述物理量变化的微分关系式。最后，再利用积分这个数学工具，将这个微观的关系式推广到宏观的整条平带上。

如图，选取一小段平带作为分析对象平带微元，这段平带非常短，它所对应的圆心角也极其微小，称之为 $\mathrm{d}\theta$。假设平带即将像左侧滑动，那么左侧的张力会更大。作用在微元上的力有：

• 右侧张力 ($T$)：微元的右侧平带对它施加的拉力。

• 左侧张力 ($T+\mathrm{d}T$)：微元的左侧平带对它施加的拉力。因为张力是沿着平带逐渐增大的，所以在经过 $\mathrm{d}\theta$ 这个微小角度后，张力会有一个微小的增量 $\mathrm{d}T$。

• 法向力 ($\mathrm{d}N$)：曲面垂直于接触面，对这个微元施加的支持力。因为研究对象是微元，所以这个力也是一个微小的量 $\mathrm{d}N$。

• 摩擦力 ($\mathrm{d}F$)：作用在接触面上，方向与即将滑动的方向（向左）相反，所以向右。因为分析的是“即将滑动”的临界状态，所以此时的摩擦力为最大静摩擦力，其大小为 $\mathrm{d}F={\mu }_s\mathrm{d}N$。这也是一个微小的量。

建系并列出等式

如图，建立 $x,y$ 坐标轴。根据平衡公式可得：

$$\{\begin{array}{rl}T\cos (\frac{\mathrm{d}\theta }{2})+\mu \mathrm{d}N-(T+\mathrm{d}T)\cos (\frac{\mathrm{d}\theta }{2})& =0\\ \mathrm{d}N-(T+\mathrm{d}T)\sin (\frac{\mathrm{d}\theta }{2})-T\sin (\frac{\mathrm{d}\theta }{2})& =0\end{array}$$

• 简化：

  • $\frac{\mathrm{d}\theta }{2}$ 是一个微小的量，所以 $\sin (\frac{\mathrm{d}\theta }{2})\approx \frac{\mathrm{d}\theta }{2}$，$\cos (\frac{\mathrm{d}\theta }{2})\approx 1$。

  • 类似地，$\mathrm{d}T$ 和 $\frac{\mathrm{d}\theta }{2}$ 的乘积可忽略不计 ($\approx 0$)。

经过简化后的式子为：

$$\{\begin{array}{rl}\mu \mathrm{d}N& =\mathrm{d}T\\ \mathrm{d}N& =T\mathrm{d}\theta \end{array}$$

• 简化后的 $x$ 轴方向的受力分析可以看出：张力的微小增量完全是由于摩擦力产生的。

• 简化后的 $y$ 轴方向的受力分析可以看出：张力越大，对曲面的压力就越大。

消去 $\mathrm{d}N$，可得：

$$\frac{\mathrm{d}T}{T}=\mu \mathrm{d}\theta$$

对上式左右两边同时进行积分，可得：

$$\begin{array}{rl}{\int }_{T_1}^{T_2}\frac{\mathrm{d}T}{T}& =\mu {\int }_0^{\beta }\mathrm{d}\theta \\ \ln \frac{T_2}{T_1}& =\mu \beta \\ T_2& =T_1{e}^{\mu \beta }\end{array}$$

• $T_2,T_1$：平带张力；$T_1$ 抵抗平带相对于接触面的运动（或即将发生的运动）方向，而 $T_2$ 则作用于平带相对运动（或即将发生的运动）方向。由于摩擦力的缘故有， $T_2>T_1$。

• $\mu$：平带与接触面之间的静摩擦或动摩擦系数。

• $\beta$：平带与表面的接触角度，以弧度 (radians) 为单位测量。

• $e$：2.718...，自然对数的底数。

注意，$T_2$ 的值与接触面的半径 $r$ 无关，它仅取决于平带与表面的接触角 $\beta$。因此，这个公式适用于缠绕在任何形状的曲面上的平面皮带。

轴承

Bearings

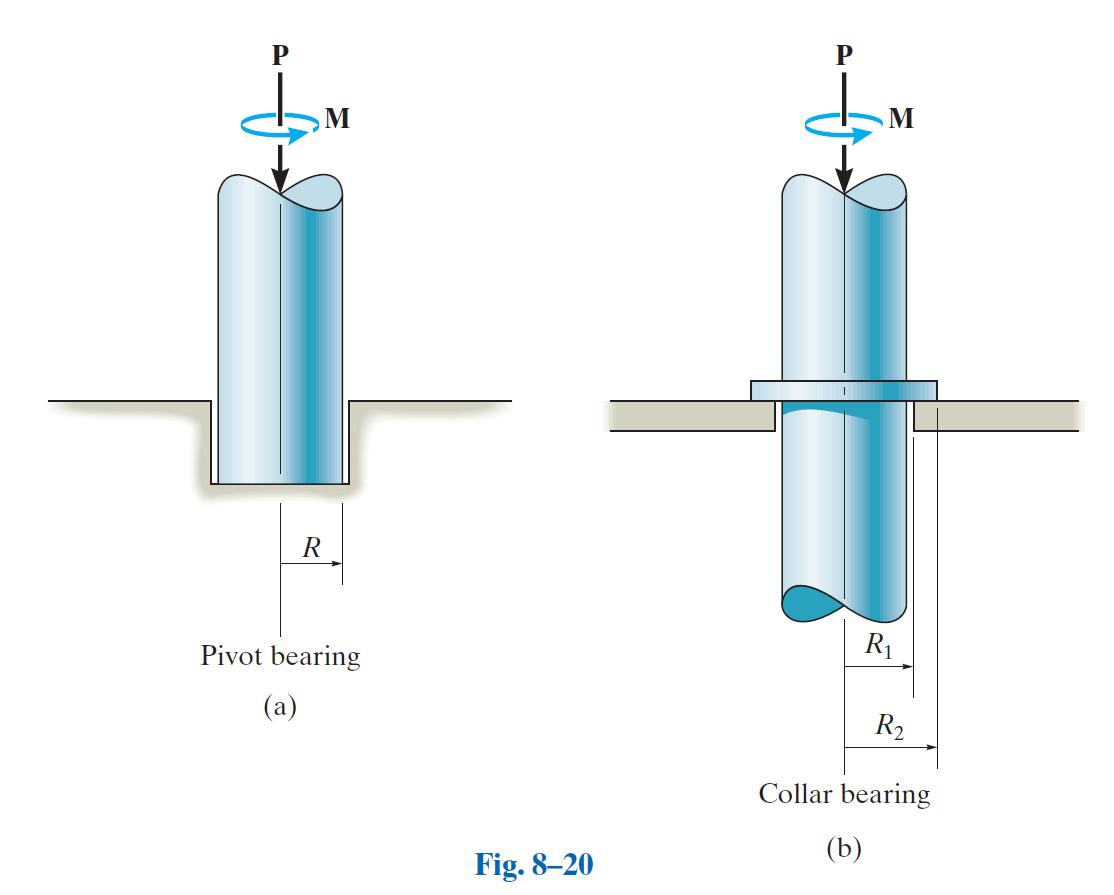
止推轴承

Collar Bearing

核心思路：微元法

Method of Differential Elements

分析轴承摩擦的核心思想是采用微元法。我们将整个接触面分割成无数个微小的面积单元 $dA$，分析单个微元上的受力情况，然后通过积分将所有微元产生的效果叠加起来，从而求得总的摩擦力矩。

基本假设

1. 载荷均匀分布: 施加于轴承上的轴向载荷 $P$ 均匀地分布在整个接触面上。因此，接触面各处的压强 $p$ 是一个常量。
2. 摩擦系数恒定: 接触面上的静摩擦系数 ${\mu }_s$ 是一个常量。

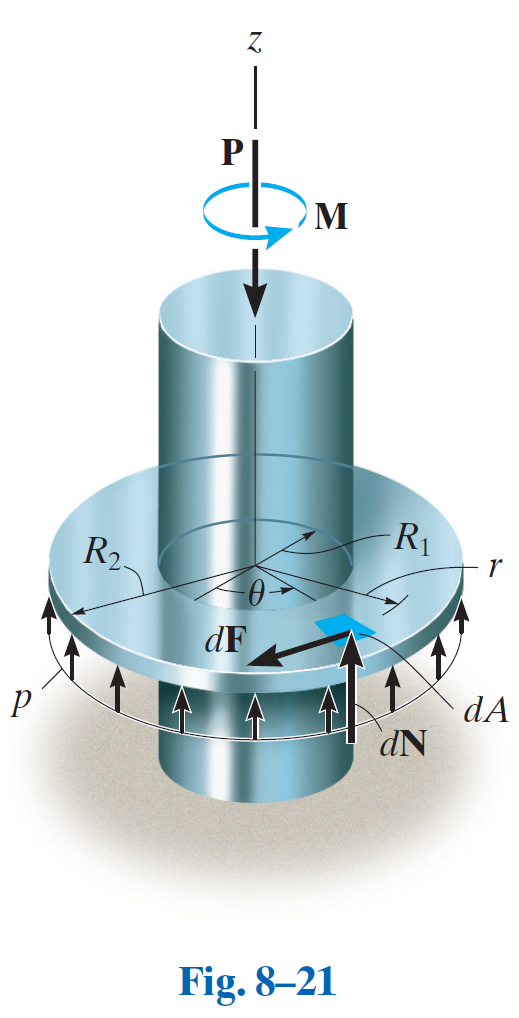
对于一个内径为 $R_1$、外径为 $R_2$ 的空心圆环形止推轴承，其抵抗转动的最大摩擦力矩 $M$ 的推导过程如下：

1. 计算压强 (Pressure, $p$) 接触面积 $A=\pi (R_2^2-R_1^2)$。 根据假设1，压强 $p$ 为：

   $$p=\frac{P}{A}=\frac{P}{\pi (R_2^2-R_1^2)}$$

2. 选取微元并分析受力 我们在圆环面上任意位置取一个极小的面积微元 $dA$。在极坐标下，这个微元的面积可以表示为：

   $$\mathrm{d}A=(r\mathrm{d}\theta )\mathrm{d}r$$

   这个微元上所受到的法向力 $dN$ 为：

   $$\mathrm{d}N=p\mathrm{d}A$$

   当轴承即将发生转动时，该微元受到的最大静摩擦力 $dF$ 为：

   $$\mathrm{d}F={\mu }_s\mathrm{d}N$$

3. 计算微元力矩 (Moment of the Differential Force) 这个摩擦力 $dF$ 距离转动中心（圆心）的距离为 $r$。因此，它产生的抵抗力矩 $dM$ 为：

   $$\mathrm{d}M=r\mathrm{d}F$$

4. 积分求和 (Integration) 为了得到整个接触面产生的总摩擦力矩 $M$，我们需要对 $dM$ 进行二重积分。积分变量 $r$ 的范围是从 $R_1$ 到 $R_2$，$\theta$ 的范围是从 $0$ 到 $2\pi$。

   $$\begin{array}{rl}M& ={\int }_{A}r\mathrm{d}F\\ & ={\int }_{R_1}^{R_2}{\int }_0^{2\pi }r\left[\frac{{\mu }_{s}P}{\pi (R_2^2-R_1^2)}\right](r\mathrm{d}\theta \mathrm{d}r)\\ & =\frac{{\mu }_{s}P}{\pi (R_2^2-R_1^2)}{\int }_{R_1}^{R_2}{r}^2\mathrm{d}r{\int }_0^{2\pi }\mathrm{d}\theta \end{array}$$

   化简后得到最终的公式：

   $$M=\frac{2}{3}{\mu }_{s}P\left(\frac{R_2^3-R_1^3}{R_2^2-R_1^2}\right)$$

   这个公式计算了使轴承开始转动所需克服的最大摩擦力矩。

枢轴轴承

Pivot Bearing

对于枢轴轴承的情况，在止推轴承公式的基础之上，取 $R_2=R$ 和 $R_1=0$，可得公式：

$$M=\frac{2}{3}{\mu }_{s}PR$$

关于压强分布的重要说明

上述推导的公式仅在 压强 $p$ 恒定 (constant pressure) 的假设下成立。

如果压强不是均匀分布的，但在积分求力矩之前，可以先确定压强 $p$ 作为接触面位置的函数表达式（例如 $p(r,\theta )$），那么依然可以求解。此时，需要将变化的压强函数代入积分表达式中：

$$M={\int }_{A}r{\mu }_s(p(r,\theta )\mathrm{d}A)={\mu }_s{\int }_{R_1}^{R_2}{\int }_0^{2\pi }{r}^{2}p(r,\theta )\mathrm{d}\theta \mathrm{d}r$$

径向轴承

Journal Bearing

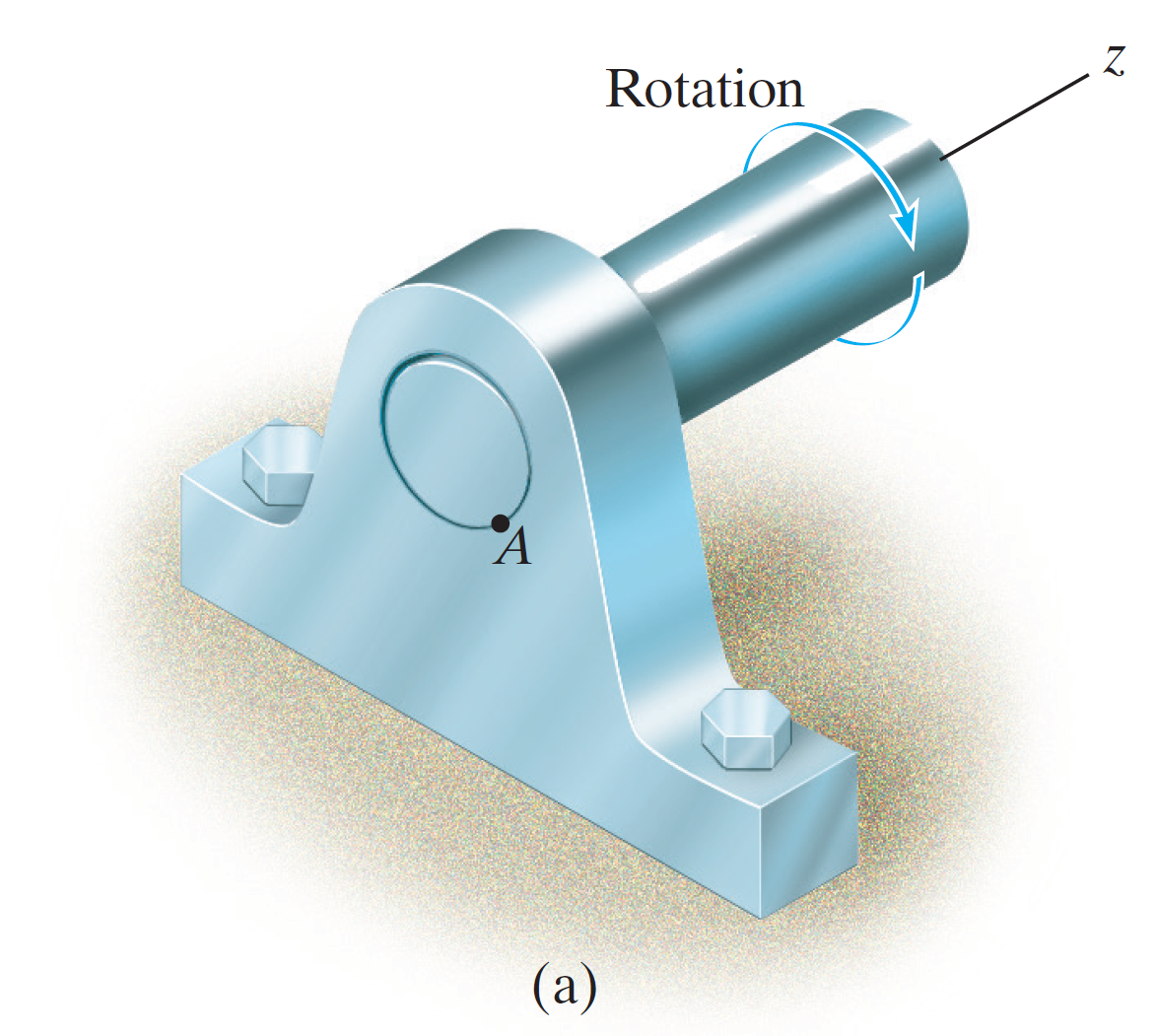
功能与模型

径向轴承用于支撑径向载荷 (radial load)，即垂直于轴线的力。模型由一个半径为 $r$ 的轴颈 (journal) 和一个半径略大的轴承 (bearing) 组成。

基本假设

1. 刚体与点接触 (Rigid Body & Point Contact): 基于刚体假设，轴颈和轴承之间的接触被简化为在单个点上。现实中这是一个微小的接触面，但在刚体模型中我们将其理想化为一个点，以便进行力学分析。
2. 匀速转动状态 (State of Uniform Motion): 此模型计算的是维持轴颈以缓慢、恒定角速度转动所需的力矩 $M$。因此，分析中使用的是动摩擦系数 ${\mu }_k$。

受力分析与摩擦圆

在未施加力矩时，轴颈与轴承的接触点 $A$ 位于最低点。当施加力矩 $M$ 使轴颈转动时，轴颈会沿轴承内壁向上“爬升”，使接触点 $A$ 移动一个微小的角度。此时，轴承对轴颈的反作用力 $R$ 由法向力 $N$ 和动摩擦力 $F$ 组成，其中 $F={\mu }_{k}N$。

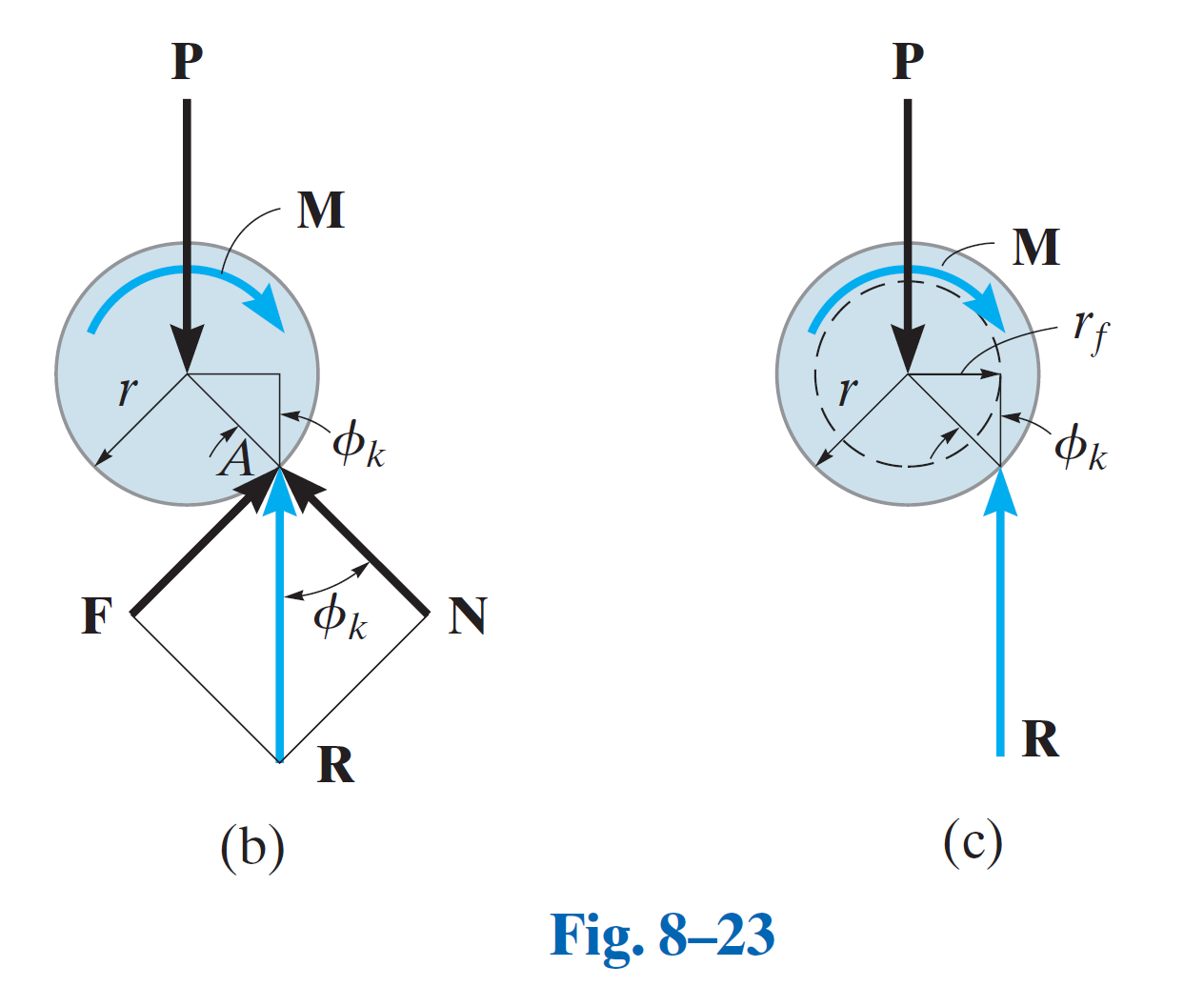
为了使系统保持平衡，反作用力 $R$ 必须与外部载荷 $P$ 大小相等、方向相反。由于摩擦力的存在，$R$ 的作用线不再通过轴颈的中心，而是与一个以轴心为圆心、半径为 $r_f$ 的小圆相切。这个圆被称为摩擦圆 (Friction Circle)。

摩擦圆的半径 $r_f$ 为：

$$r_f=r\sin {\varphi }_k$$

其中 ${\varphi }_k$ 是动摩擦角，满足 $\tan {\varphi }_k={\mu }_k$。

力矩推导

为了维持匀速转动，外加力矩 $M$ 必须平衡由反作用力 $R$ 产生的摩擦力矩。该力矩的大小等于 $R$ 的大小乘以其力臂（即摩擦圆的半径 $r_f$）。

$$M=R\cdot r_f=R(r\sin {\varphi }_k)$$

根据力的平衡条件，$R=P$，因此：

$$M=Pr\sin {\varphi }_k$$

工程近似 (Engineering Approximation)

在多数工程应用中，摩擦系数 ${\mu }_k$ 很小，导致摩擦角 ${\varphi }_k$ 也很小。根据小角度近似 ($\sin {\varphi }_k\approx \tan {\varphi }_k={\mu }_k$)，公式可简化为：

$$M\approx Pr{\mu }_k$$

滚动阻力

Rolling Resistance

核心思路

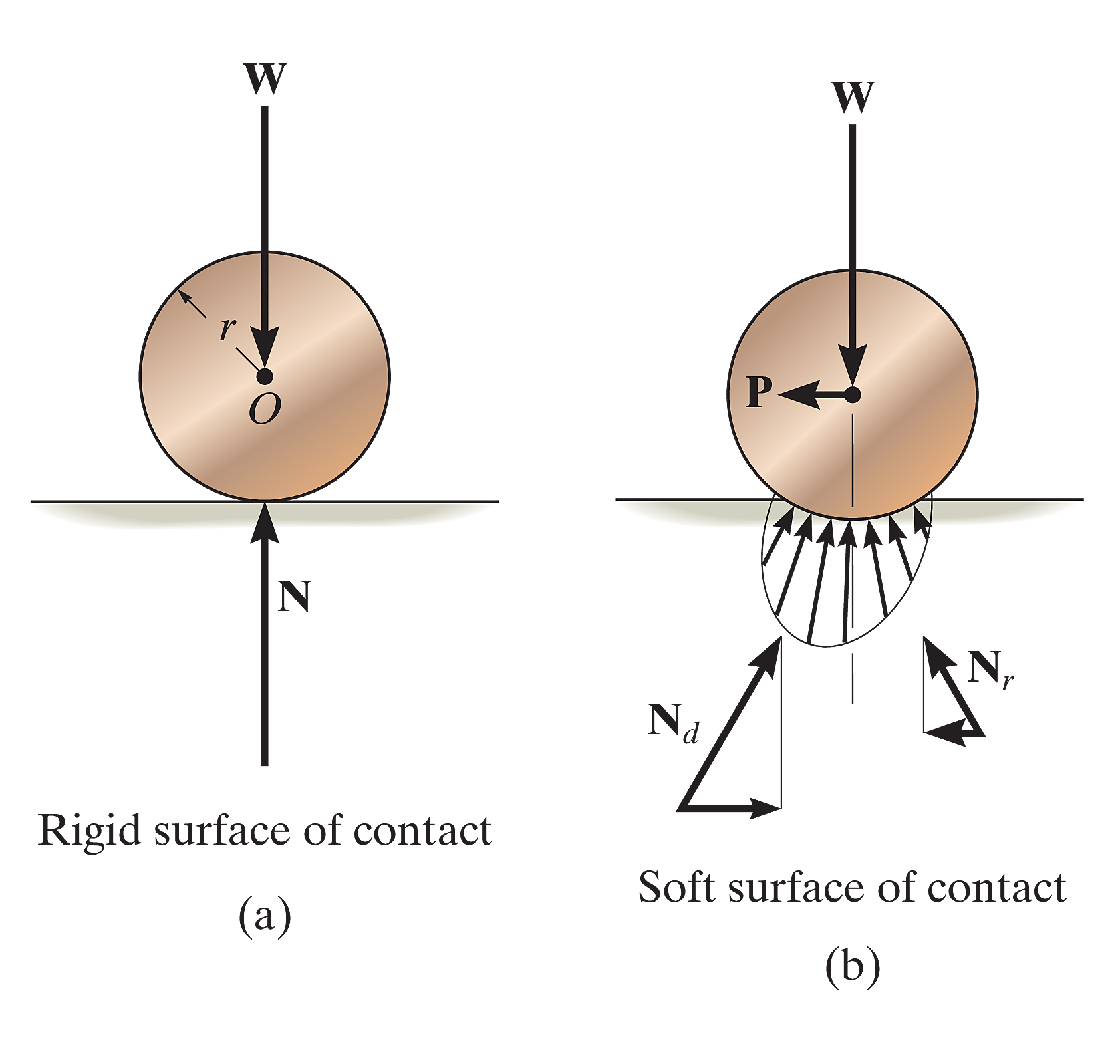
滚动阻力的根本原因在于接触面的局部变形 (local deformation)。当刚性滚动体（如车轮）在较软的表面（如土地）上滚动时，其前方的材料被压缩变形，产生一个阻碍运动的变形力 ($N_d$)；其后方的材料则从变形中恢复，产生一个推动运动的恢复力 ($N_r$)。

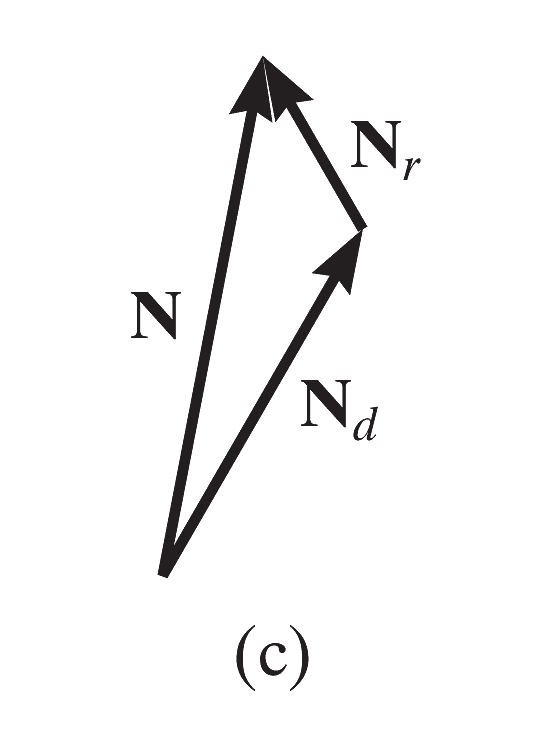
由于材料变形过程中的能量损失（例如内摩擦），变形力 $N_d$ 及其水平分量总是大于恢复力 $N_r$ 及其水平分量。这导致地面对滚动物体的总法向反作用力 $N$（即 $N_d$ 和 $N_r$ 的合力）的作用点会向前偏移，从而产生一个抵抗滚动的力矩，这个力矩必须由一个外部推力 $P$ 来平衡。

理想模型

一个刚性的、完美的圆柱体或球体，在一个可变形的、较软的平面上，受到一个水平力 $P$ 的作用，以缓慢且恒定的速度进行纯滚动。

基本假设

1. 滚动体是刚体: 假设轮子本身在受力后不发生任何形变。
2. 接触面是可变形的: 与轮子接触的地面或轨道会发生形变。
3. 匀速滚动: 分析的情景是轮子克服滚动阻力，以恒定速度滚动。因此，系统处于力的平衡状态。

关键术语

• 滚动阻力系数 (Coefficient of Rolling Resistance), $a$:
  • 物理意义: 它代表了由于地面变形，地面对轮子的总反作用力 $N$ 的作用点，相较于轮子几何中心正下方位置的水平前移距离。
  • 单位: 它是一个长度量纲，单位通常是米(m)、毫米(mm)或英寸(in)。
  • 区别: 它与无量纲的滑动摩擦系数 (${\mu }_s$, ${\mu }_k$) 在物理意义和单位上完全不同。

受力分析

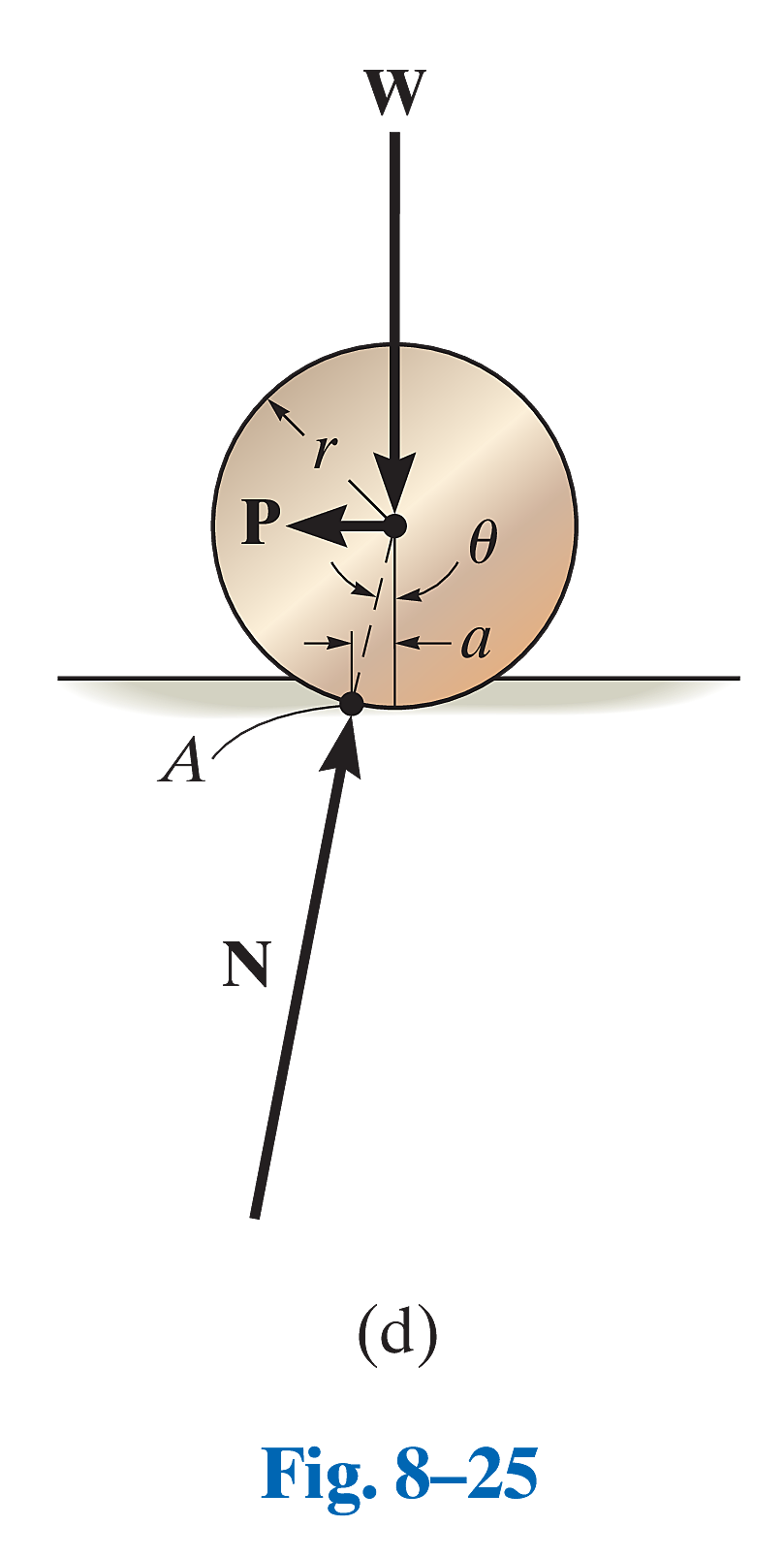
对处于匀速滚动状态的圆柱体进行受力分析，主要考虑以下几个力：

• 圆柱体重量 $W$，作用于圆心 $O$，方向竖直向下。
• 水平推力 $P$，通常假设其作用于圆心 $O$。
• 地面的总反作用力 $N$ (是 $N_d$ 与 $N_r$ 的合力)，由于地面变形，其作用点 $A$ 向前偏移了距离 $a$。

数学公式

维持圆柱体匀速滚动所需克服滚动阻力的水平推力 $P$ 可以通过力矩平衡推导得出。

1. 力矩平衡 (Moment Equilibrium): 因为圆柱体匀速滚动，所以它处于平衡状态，其所受合力矩为零。为简化计算，我们选取地面支持力 $N$ 的作用点 $A$ 作为力矩中心，则 $\sum M_A=0$。

   • 重量 $W$ 产生的力矩为 $W\cdot a$ (该力矩阻碍滚动)。
   • 推力 $P$ 产生的力矩为 $P\cdot r^{\prime }$ (该力矩驱动滚动)，其中 $r^{\prime }$ 是点 $A$ 到推力 $P$ 作用线的垂直距离。

2. 推导与近似: 建立力矩平衡方程 (通常定义驱动力矩为正)：

   $$\sum M_A=P\cdot r^{\prime }-W\cdot a=0$$

   在大多数情况下，变形量很小，滚动阻力系数 $a$ 远小于半径 $r$ ($a\ll r$)。因此，我们可以近似认为力臂 $r^{\prime }\approx r$。同时，在竖直方向上，力的平衡近似给出 $N\approx W$。 将 $r^{\prime }\approx r$ 代入力矩平衡方程：

   $$P\cdot r\approx W\cdot a$$

   整理后得到最终的近似公式：

   $$P\approx \frac{Wa}{r}$$

示例

F8-1. ~ F8-9. 题目

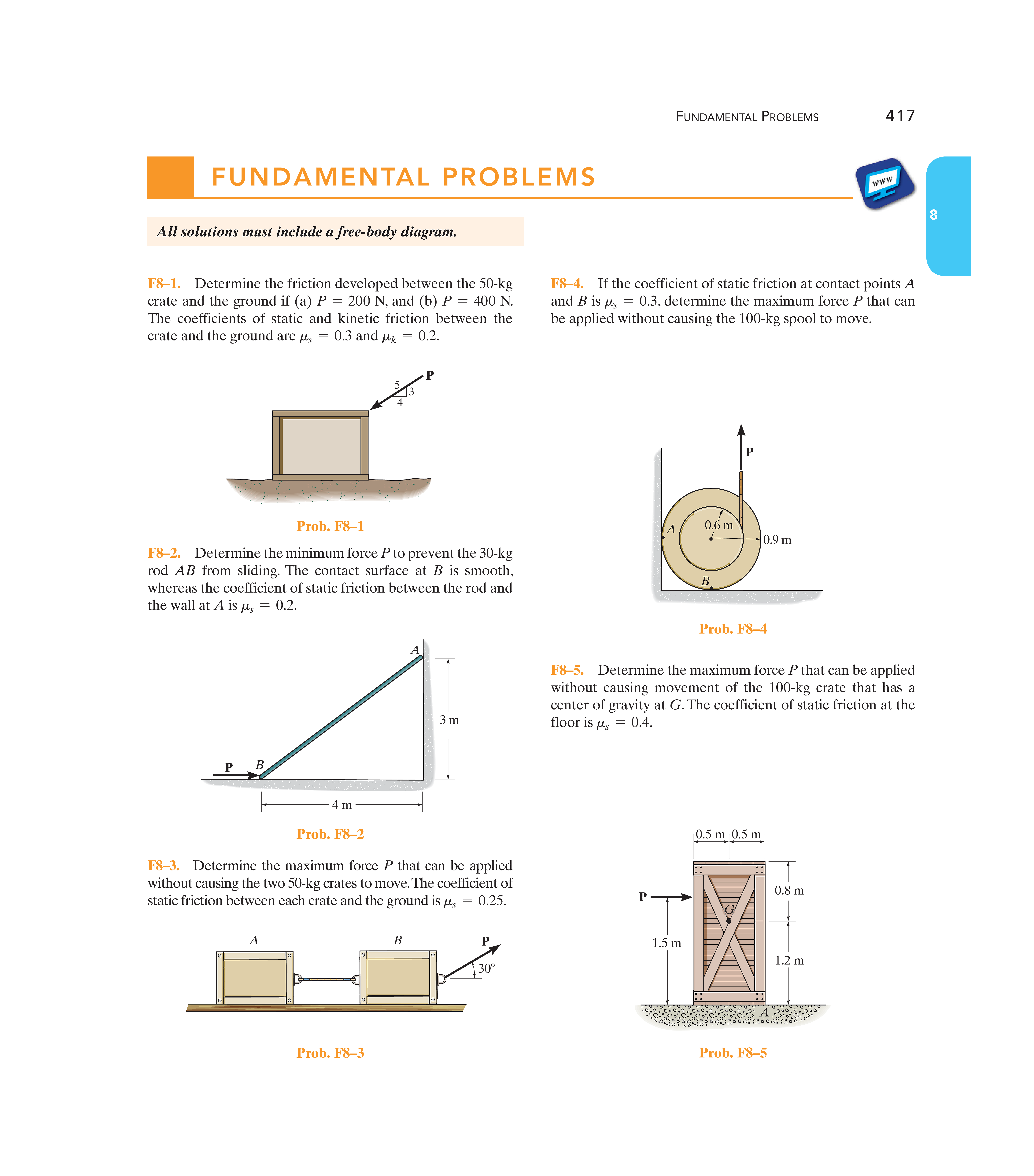
F8-1. ~ F8-9. 解题

尝试使用 MMA 解题

frictionForP[p_?NumericQ, label_:""] :=
    Module[{muS = 0.3, muK = 0.2, m = 50, theta = ArcTan[3/4], pX, pY,
         w, n, fSMax, fK, friction, frictionType},
        pX = p * Cos[theta];
        pY = p * Sin[theta];
        w = m * 9.81;
        n = w + pY;
        fSMax = muS * n;
        fK = muK * n;
        If[Abs[pX] <= fSMax,
            friction = Abs[pX];
            frictionType = "static";
            ,
            friction = fK;
            frictionType = "kinetic";
        ];
        If[StringLength[label] > 0,
            Print[label, " ", "Friction = ", ToString[NumberForm[N[friction
                ], {8, 2}]], " N; (", frictionType, " friction);"];
            ,
            Print["Friction = ", ToString[NumberForm[N[friction], {8,
                 2}]], " N; (", frictionType, " friction);"];
        ];
        friction
    ];

Print["F8-1:"];

f8p1a = frictionForP[200, "(a)"];

f8p1b = frictionForP[400, "(b)"];

f8p2 =
    Module[{muS = 0.2, ob = 4, oa = 3, m = 30, Pvar, nA, w, fS, nB, momentO,
         sol, pVal},
        nA = Pvar;
        w = m * 9.81;
        fS = muS * nA;
        nB = w - fS;
        momentO = nA * oa - nB * ob + w * (ob / 2);
        sol = Solve[momentO == 0, Pvar];
        pVal = N[Pvar /. sol[[1]]];
        Print["F8-2:"];
        Print["Pmin = ", ToString[NumberForm[pVal, {8, 2}]], " N;"];
        pVal
    ];

f8p3 =
    Module[{muS = 0.25, mA = 50, mB = 50, g = 9.81, theta = 30 Degree,
         Pvar, wA, wB, eq, sol, symP, pVal, nBVal},
        wA = mA * g;
        wB = mB * g;
        eq = Pvar * Cos[theta] == muS * (wA + wB - Pvar * Sin[theta])
            ;
        sol = Solve[eq, Pvar];
        symP = Simplify[Pvar /. sol[[1]]];
        pVal = N[symP];
        nBVal = wB - pVal * Sin[theta];
        If[nBVal <= 0,
            Print["F8-3: Warning \[LongDash] normal on B <= 0 at computed P_max; contact may lift."
                ]
        ];
        Print["F8-3:"];
        Print["Pmax = ", ToString[NumberForm[pVal, {8, 2}]], " N;"];
        pVal
    ];

f8p4 =
    Module[{muS = 0.3, mass = 100, gravity = 9.81, rInner = 0.6, rOuter
         = 0.9, weight, eqX, eqY, eqM, sol, na, nb, p},
        weight = mass * gravity;
        eqX = na - muS * nb == 0;
        eqY = p - weight + muS * na + nb == 0;
        eqM = p * rInner - muS * na * rOuter - muS * nb * rOuter == 0
            ;
        sol = Solve[{eqX, eqY, eqM}, {na, nb, p}];
        p = N[p /. sol[[1]]];
        Print["F8-4:"];
        Print["Pmax = ", ToString[NumberForm[p, {8, 2}]], " N;"];
        pVal
    ];

f8p5 =
    Module[{mass = 100, gravity = 9.81, muS = 0.4, normal, weight, p,
         frictionMax, eqM, sol, ans},
        weight = mass * gravity;
        normal = weight;
        frictionMax = muS * normal;
        ans = frictionMax;
        eqM = -p * 1.5 + normal * 0.5 == 0;
        sol = Solve[eqM, p];
        ans = Min[ans, p /. sol[[1]]];
        Print["F8-5:"];
        Print["Pmax = ", ToString[NumberForm[ans, {8, 2}]], " N;"];
        ans
    ];

f8p6 =
    Module[{mass = 50, gravity = 9.81, normal, rInner = 0.3, rOuter =
         0.6, theta = 60 Degree, tension, friction, muS, weight, eqY, eqX, eqM,
         sol, vars},
        weight = mass * gravity;
        eqY = tension * Cos[theta] + friction == weight;
        eqX = tension * Sin[theta] == normal;
        eqM = -tension * rInner + friction * rOuter == 0;
        sol = Solve[{eqY, eqX, eqM}, {tension, friction, normal}];
        Print["F8-6:"];
        vars = sol[[1]];
        muS = (friction /. vars) / (normal /. vars);
        Print["muS = ", ToString[NumberForm[N[muS], {8, 3}]]];
    ];

f8p7 =
    Module[{weightA = 50, weightB = 25, weightC = 15, gravity = 9.81,
         muAB = 0.3, muBC = 0.4, muCD = 0.35, ans},
        ans = Min[muAB * weightA + muBC * (weightA + weightB), muAB *
             weightA + muCD * (weightA + weightB + weightC)];
        Print["F8-7:"];
        Print["The smallest horizontal force P = ", ToString[NumberForm[
            N[ans], {8, 2}]], " N;"];
        ans
    ];

f8p8 =
    Module[{muS, theta, weight, tension, ans},
        equasions = {weight * Sin[theta] == tension + muS * weight * 
            Cos[theta], weight * Sin[theta] + muS * (weight * 3 * Cos[theta]) == 
            tension * 2};
        sol = Solve[equasions, {theta, tension}];
        Print["F8-8:"];
        (* Print[sol]; *)
        ans = "ArcTan[1/Sqrt[1 + 25 muS^2], (5 muS)/Sqrt[1 + 25 muS^2]]"
            ;
        Print["theta = ", ans];
        ans
    ];

f8p9 =
    Module[{massA = 7, massB = 10, gravity = 9.81, muAB = 0.3, muA = 
        0.1, pull, frictionAB, frictionA, weightA, weightB},
        weightA = massA * gravity;
        weightB = massB * gravity;
        frictionAB = muAB * weightB;
        frictionA = muA * (weightA + weightB);
        pull = Min[frictionAB, frictionA];
        pull = Min[pull, weightB * 0.15 / 0.4];
        Print["F8-9:"];
        Print["The maximum horizontal pull P = ", ToString[NumberForm[
            N[pull], {8, 2}]], " N;"];
        pull
    ];

输出：

F8-1:

(a) Friction = 160.00 N; (static friction);

(b) Friction = 146.10 N; (kinetic friction);

F8-2:

Pmin = 154.89 N;

F8-3:

Pmax = 247.47 N;

F8-4:

Pmax = 342.62 N;

F8-5:

Pmax = 327.00 N;

F8-6:

muS = 0.577

F8-7:

The smallest horizontal force P = 45.00 N;

F8-8:

theta = ArcTan[1/Sqrt[1 + 25 muS^2], (5 muS)/Sqrt[1 + 25 muS^2]]

F8-9:

The maximum horizontal pull P = 16.68 N;