力系的合力与合力矩

Forces System Resultants

力系

Forces System

一个力系是作用在某刚体上的多个力的集合：

$$\mathcal{F}=\{({\mathbf{F}}_1,{\mathbf{r}}_1),({\mathbf{F}}_2,{\mathbf{r}}_2),\cdots ,({\mathbf{F}}_n,{\mathbf{r}}_n)\}$$

其中：

• ${\mathbf{F}}_i$: 第 $i$ 个力向量
• ${\mathbf{r}}_i$: 该力的作用点相对于参考点 $O$ 的位置向量
• $\mathcal{F}$: 整个力系

力系的合力

合力为所有分力的向量和：

$${\mathbf{F}}_R=\sum _{i=1}^n{\mathbf{F}}_i$$

力系对某点的合力矩

若参考点为 $O$, 则合力矩为所有力对该点的力矩总和：

$$({\mathbf{M}}_R{)}_O=\sum _{i=1}^n{\mathbf{r}}_i\times {\mathbf{F}}_i$$

力系的简化

因此，一个力系的总效果可用一对向量表示：

$$\mathcal{F}=({\mathbf{F}}_R,({\mathbf{M}}_R{)}_O)$$

其中，${\mathbf{F}}_R$ 是合力，$({\mathbf{M}}_R{)}_O$ 是关于参考点 $O$ 的合力矩。

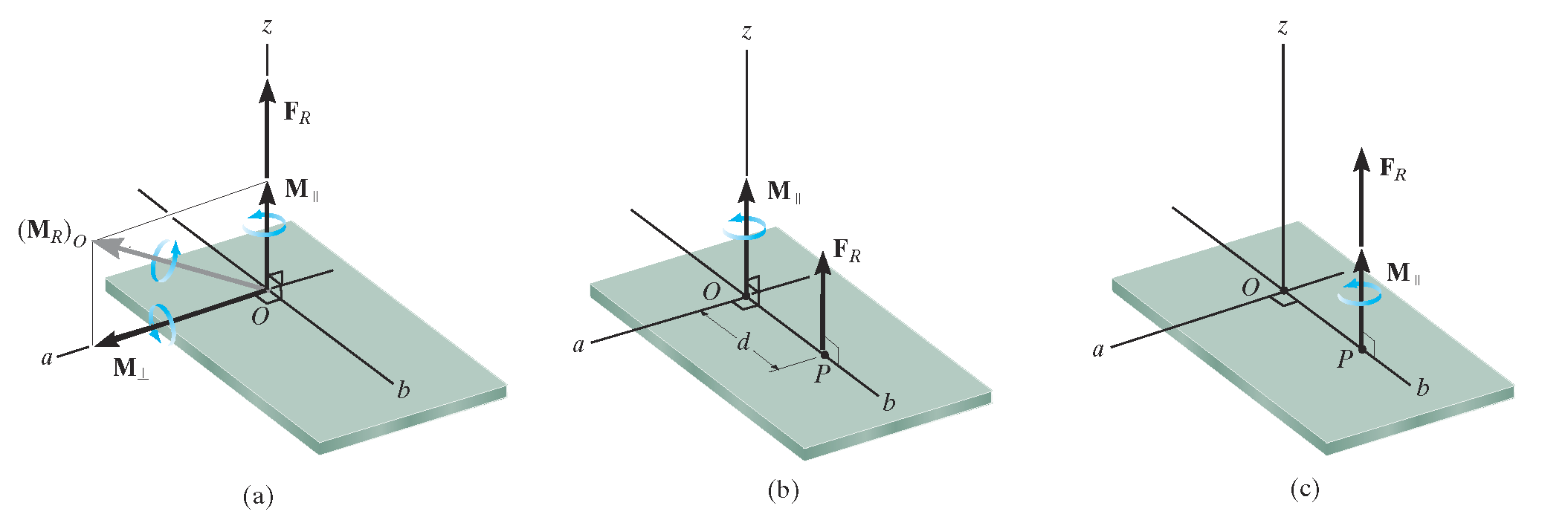
简化为力螺旋

Reduction to a Wrench

基于上述合力和合力矩，可以将整个力系进一步简化为一个力螺旋，表示为：

$$\mathcal{F}=({\mathbf{F}}_R,({\mathbf{M}}_R{)}_{\parallel },{\mathbf{r}}_{OP})$$

其中：

• $({\mathbf{M}}_R{)}_{\parallel }$ 是合力矩在合力方向上的分量。

• ${\mathbf{r}}_{OP}$ 是合力作用点 $P$ 相对于参考点 $O$ 的位置向量，满足：

$${\mathbf{r}}_{OP}\times {\mathbf{F}}_R=({\mathbf{M}}_R{)}_{\perp }$$

进一步满足：

$${\mathbf{r}}_{OP}=\frac{{\mathbf{F}}_R\times ({\mathbf{M}}_R{)}_{\perp }}{\parallel {\mathbf{F}}_R{\parallel }^2}$$

• $({\mathbf{M}}_R{)}_{\perp }$ 是合力矩中垂直于合力方向的分量。

附上教材上的图示：

简单分布载荷的简化

Reduction of a Simple Distributed Loading

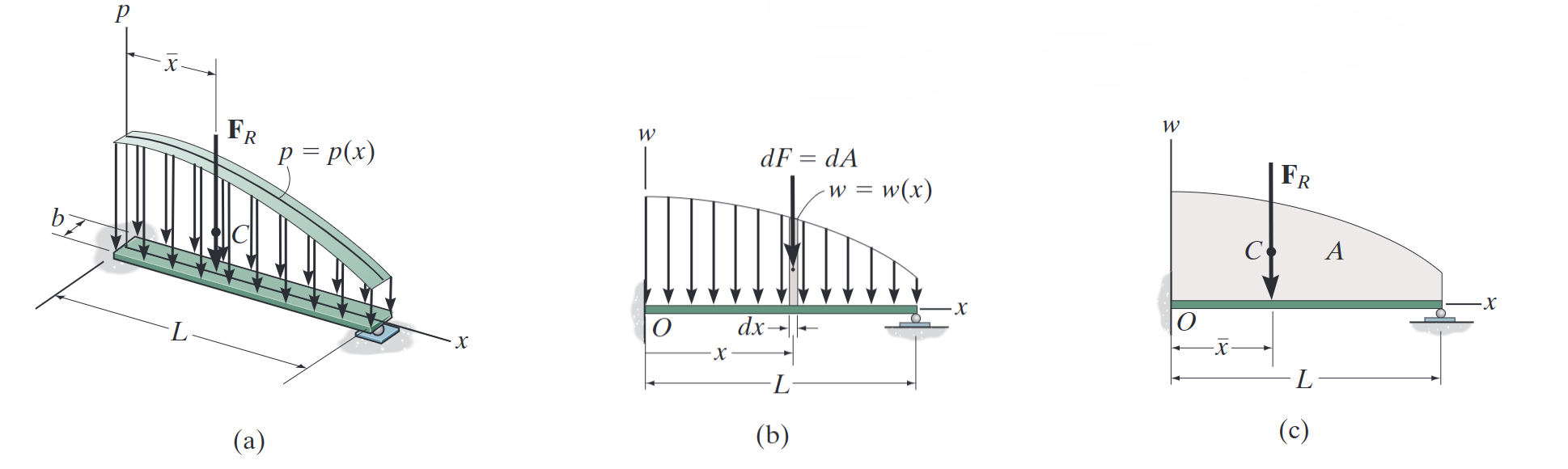
合力的计算：

$$F_R={\int }_{L}w(x)\mathrm{d}x={\int }_A\mathrm{d}A=A$$

合力作用点（重心位置）的计算：

$$\overline{x}=\frac{{\int }_{L}xw(x)\mathrm{d}x}{{\int }_{L}w(x)\mathrm{d}x}=\frac{{\int }_{A}x\mathrm{d}A}{{\int }_A\mathrm{d}A}$$

补充

力偶矩

Couple Moment

由一对力产生的力矩称为力偶矩。

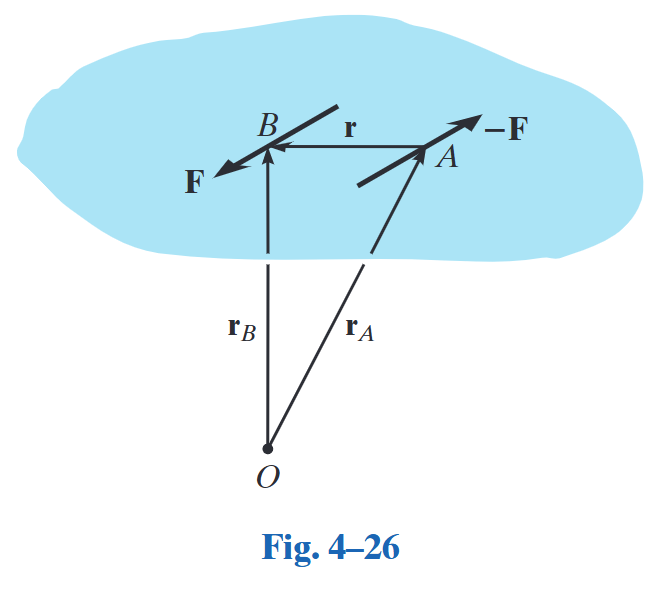
如图所示，此力偶关于参考点 $O$ 的力偶矩为：

$$\begin{array}{rl}\mathbf{M}& ={\mathbf{r}}_B\times \mathbf{F}+{\mathbf{r}}_A\times (-\mathbf{F})\\ & =({\mathbf{r}}_B-{\mathbf{r}}_A)\times \mathbf{F}\\ & =\mathbf{r}\times \mathbf{F}\end{array}$$

因此，力偶矩为自由向量 (free vector)。其大小和方向不依赖于参考点的位置，只由力偶的大小、方向和力偶之间的相对位置决定。

力偶矩通常用不带下标的符号 $\mathbf{M}$ 表示，因为力偶矩不依赖于参考点的选取。

示例