刚体的平衡
刚体的平衡公式
二维空间
三维空间
支座反力
Support Reactions
- 支座通过对物体施加力来阻止其平动。
A support prevents the translation of a body by exerting a force on the body.
- 支座通过对物体施加力偶矩来阻止其转动。
A support prevents the rotation of a body by exerting a couple moment on the body.
支座类型
以下图表是二维空间和三维空间下,常见的支座类型:
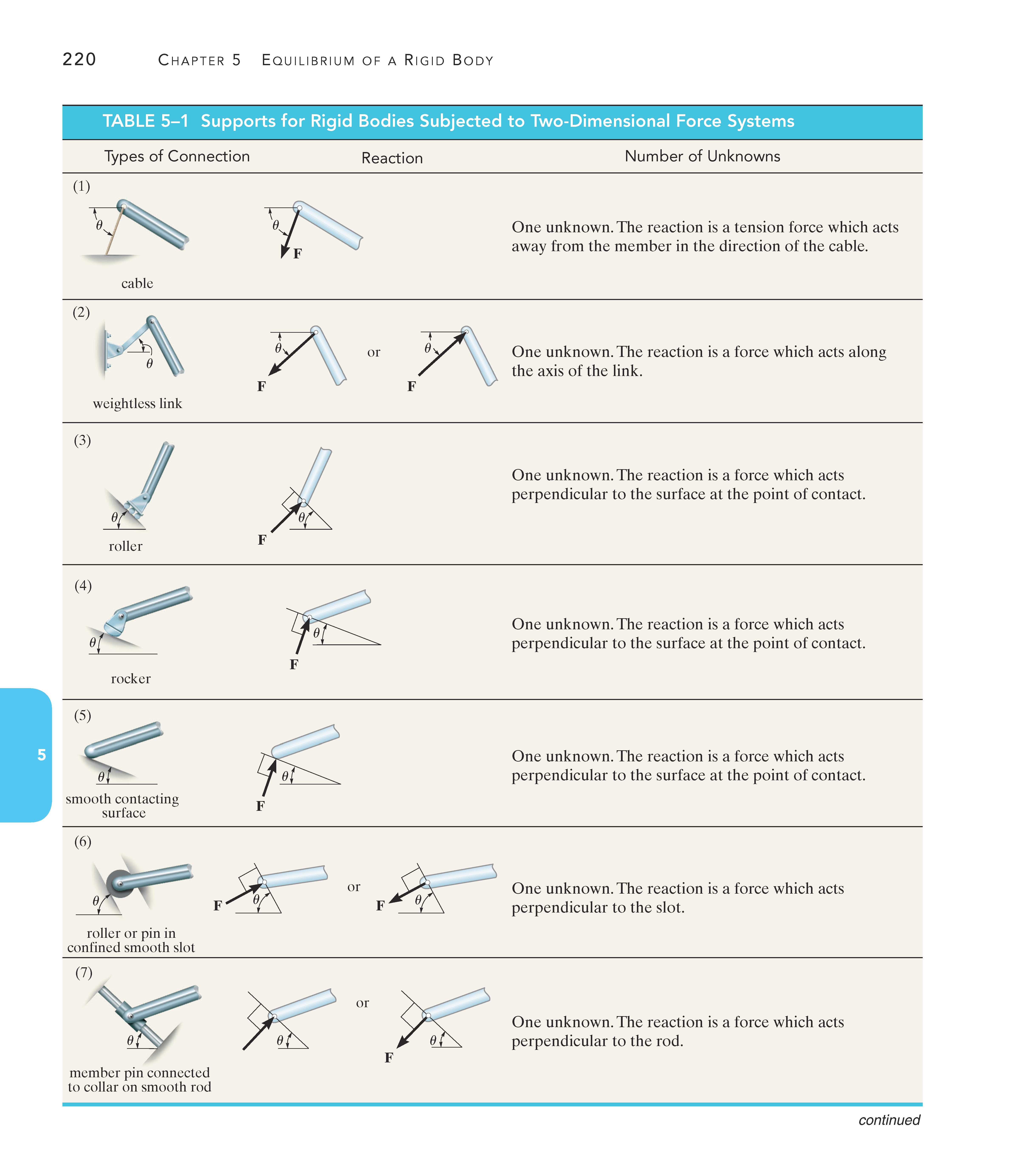 |  |
|---|
 | 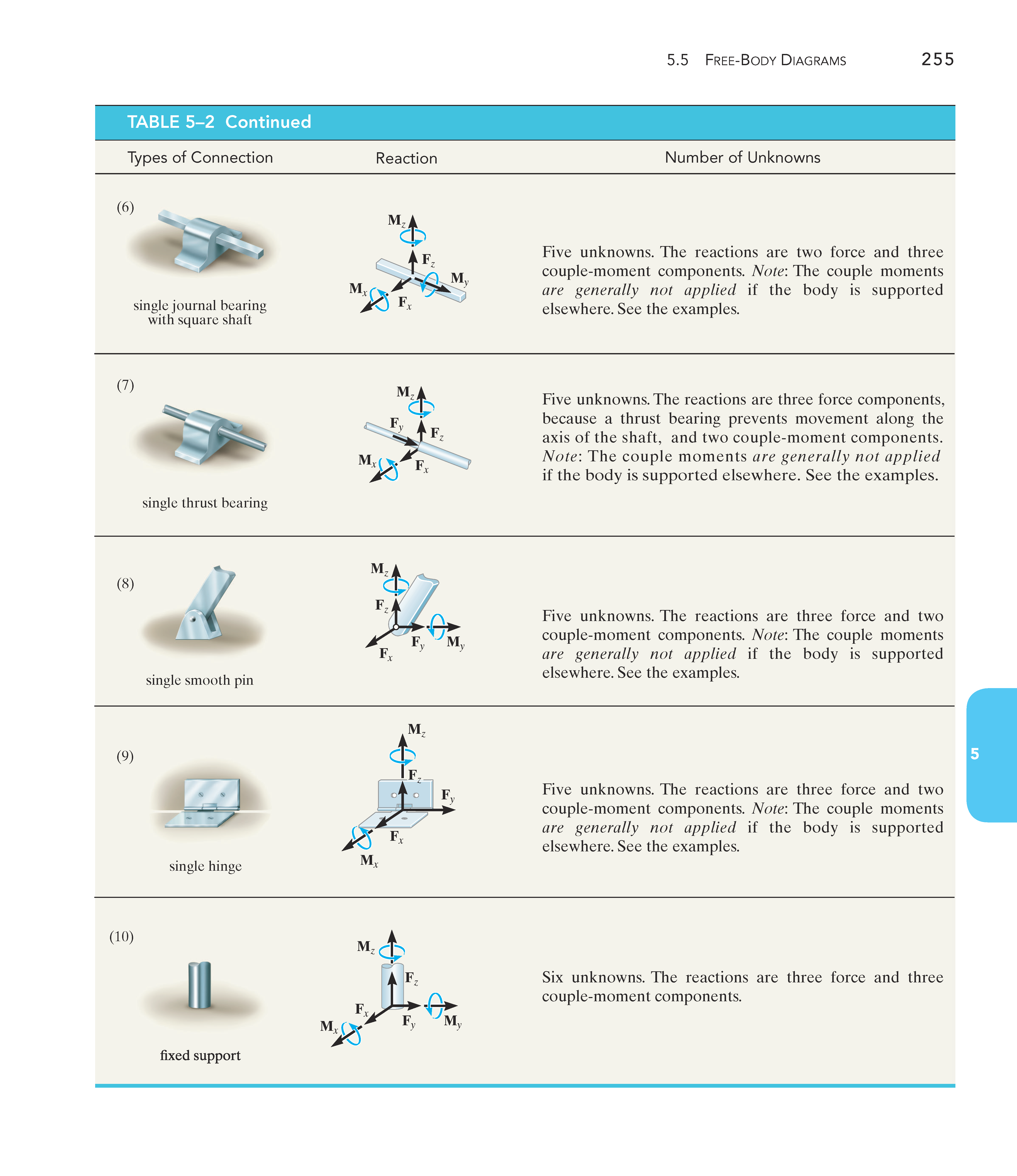 |
|---|
约束
多余约束
Redundant Constraints
不当约束
Improper Constraints
静定
Statically Determinate
静不定
Statically Indeterminate
示例
平面受力分析
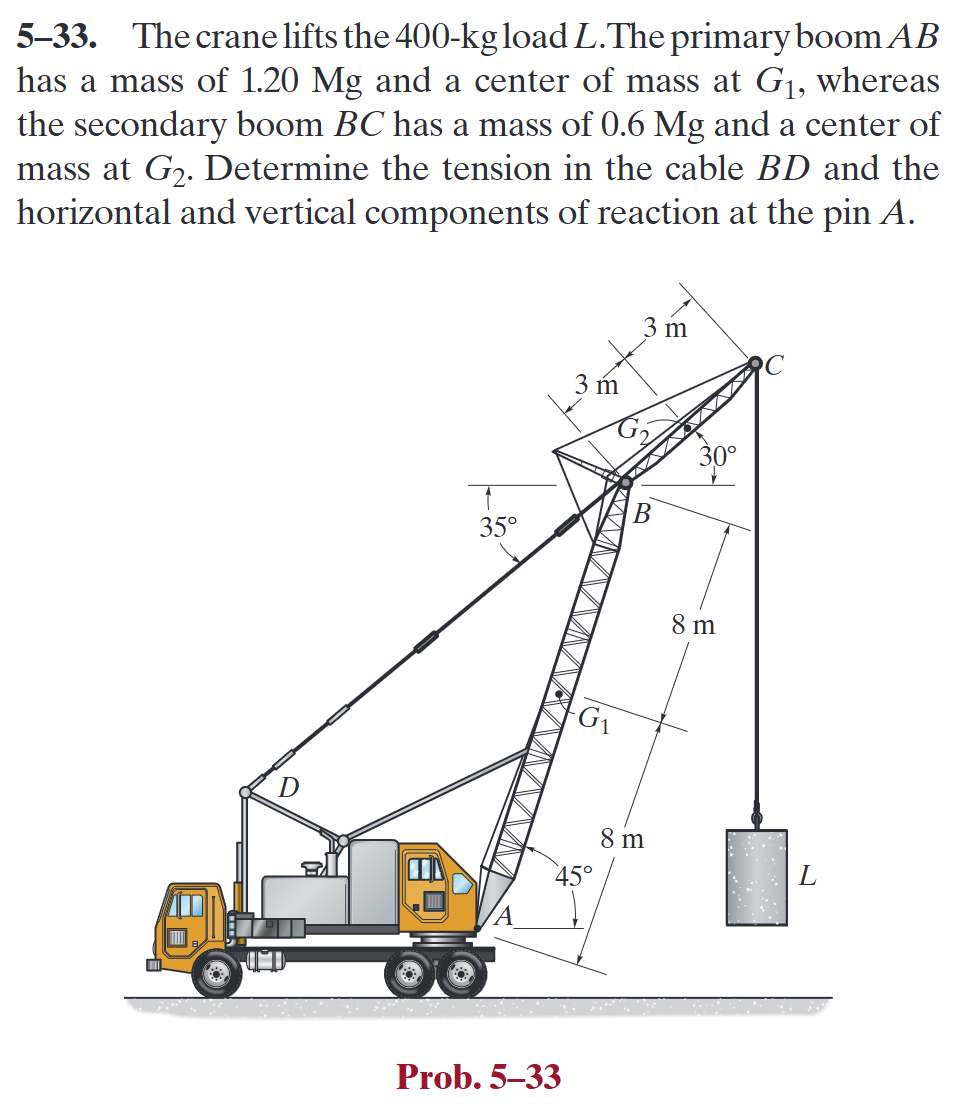
解题过程
受力分析图:
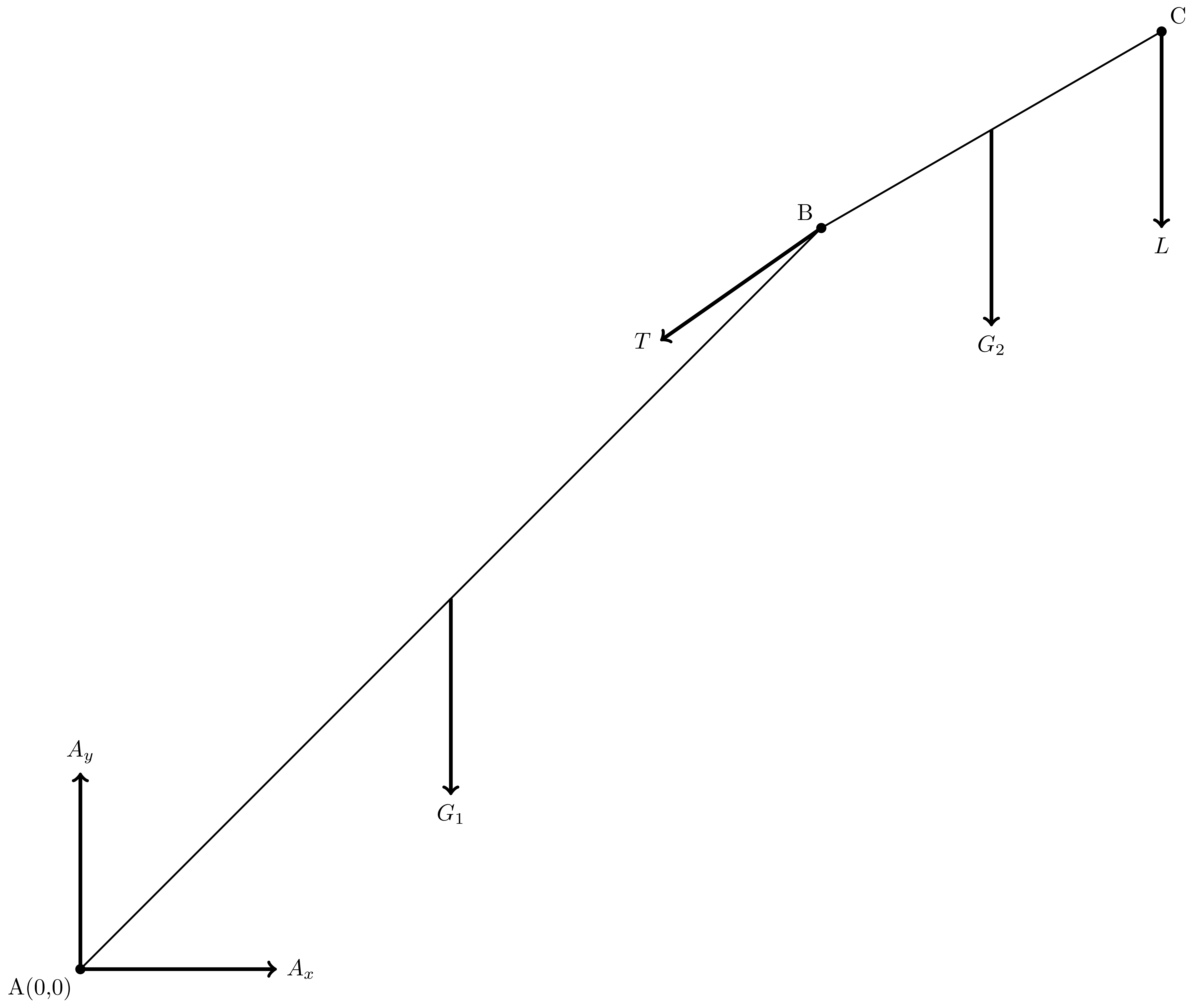
Python
"""
题目:5-33
目标:
求出刚体系统中拉力 T 和支座反力 A_x、A_y,
满足系统在力和力矩上的静力平衡。
模型说明:
- 刚体受以下外力作用:
- 向下的拉力 L,作用点偏离支座
- 两个重力 G1(1.20 吨)与 G2(0.60 吨)
- 未知方向的拉力 T(方向已知,大小未知)
- 支座反力 A,包含两个分量 A_x、A_y
- 所有力均在平面内,使用 2D 力平衡 + 1 个力矩平衡方程
方法概述:
1. 建立所有力和力矩的表达式(用向量形式)
2. 构造总合力 F_R 和总合力矩 M_R
3. 使用 sympy 的符号方程建立平衡条件(∑F = 0, ∑M = 0)
4. 利用 nsolve 数值解方程组,求解未知量
"""
import sympy as sp
# 外力:拉力 L(400 kg)
L = sp.Matrix([0, -400 * 9.8, 0])
r_L = sp.Matrix([16 * sp.cos(sp.rad(45)), 16 * sp.sin(sp.rad(45)), 0]) + \
sp.Matrix([6 * sp.cos(sp.rad(30)), 6 * sp.sin(sp.rad(30)), 0])
# 重力 G1(1200 kg)
G1 = sp.Matrix([0, -1.20e3 * 9.8, 0])
r_G1 = sp.Matrix([8 * sp.cos(sp.rad(45)), 8 * sp.sin(sp.rad(45)), 0])
# 重力 G2(600 kg)
G2 = sp.Matrix([0, -0.6e3 * 9.8, 0])
r_G2 = sp.Matrix([16 * sp.cos(sp.rad(45)), 16 * sp.sin(sp.rad(45)), 0]) + \
sp.Matrix([3 * sp.cos(sp.rad(30)), 3 * sp.sin(sp.rad(30)), 0])
# 未知量:拉力大小 T,支座反力 A_x 和 A_y
T_magnitude, A_x, A_y = sp.symbols('T_magnitude A_x A_y', real=True)
F_A = sp.Matrix([A_x, A_y, 0])
r_A = sp.Matrix([0, 0, 0]) # 以支座为原点
# 拉力 T,方向为 -145°
T = sp.Matrix([
T_magnitude * sp.cos(sp.rad(-145)),
T_magnitude * sp.sin(sp.rad(-145)),
0
])
r_T = sp.Matrix([16 * sp.cos(sp.rad(45)), 16 * sp.sin(sp.rad(45)), 0])
# 总合力与总力矩
F_R = F_A + T + L + G1 + G2
M_R = r_A.cross(F_A) + \
r_T.cross(T) + \
r_L.cross(L) + \
r_G1.cross(G1) + \
r_G2.cross(G2)
# 平衡方程:Fx = 0, Fy = 0, Mz = 0
eqs = [
sp.Eq(F_R[0], 0),
sp.Eq(F_R[1], 0),
sp.Eq(M_R[2], 0)
]
# 解方程组
sol = sp.nsolve(eqs, [T_magnitude, A_x, A_y], [1e3, 1e3, 1e3], dict=True)
# 输出结果(保留 3 位有效数字)
print(f"T: {sol[0][T_magnitude].evalf(3)} N")
print(f"A_x: {sol[0][A_x].evalf(3)} N")
print(f"A_y: {sol[0][A_y].evalf(3)} N")输出:
T: 7.67E+4 N
A_x: 6.28E+4 N
A_y: 6.55E+4 N