二阶电路

Second-Order Circuits

A second-order circuit is characterized by a second-order differential equation. It consists of resistors and the equivalent of two energy storage elements.

That the capacitor voltage and inductor current cannot change instantaneously.

\begin{aligned} v (0^{+}) & = v (0^{-}) \\ i (0^{+}) & = i (0^{-}) \end{aligned}

where t = 0^- denotes the time just before a switching event and t = 0⁺ denotes the time just after the switching event, assuming that the switching event takes place at t = 0.

无源串联 RLC 电路

The Source-Free Series RLC Circuit

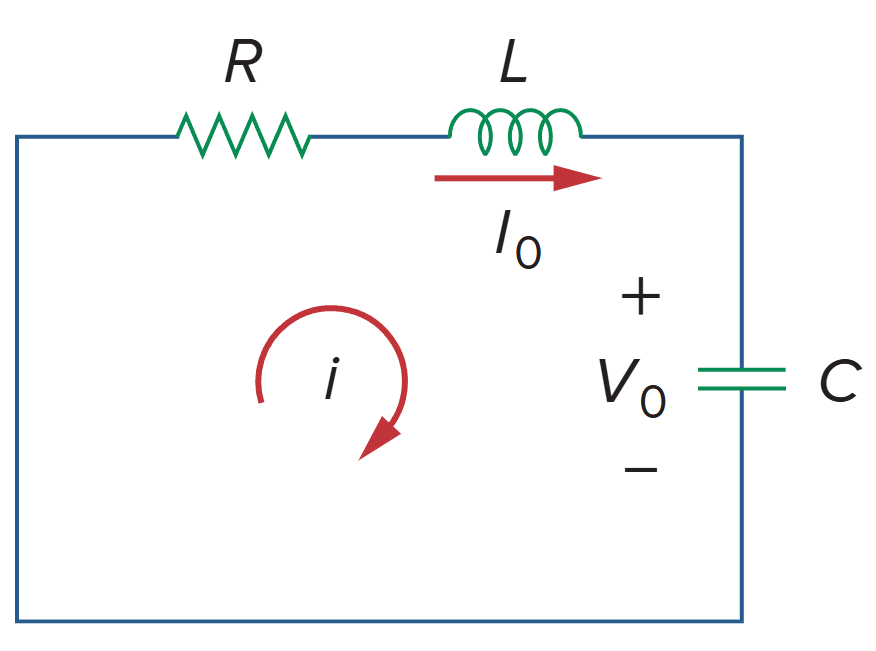
如图：

\begin{aligned} v (0) & = \frac{1}{C} \int_{- \infty}^{0} i (t) d t = V_{0} \\ i (0) & = I_{0} \end{aligned}

应用 KVL：

R i + L \frac{d i}{d t} + \frac{1}{C} \int_{- \infty}^{t} i (τ) d τ = 0

对上式的两边求关于 $t$ 的导数，得到：

\frac{d^{2} i}{d t^{2}} + \frac{R}{L} \frac{d i}{d t} + \frac{1}{L C} i = 0

这是一个二阶齐次线性微分方程。其初值条件为：

{\begin{aligned} i (0) & = I_{0} \\ \frac{d i}{d t} (0) & = - \frac{1}{L} (R I_{0} + V_{0}) \end{aligned}

通解

$α > ω_{0}$

i (t) = A_{1} e^{s_{1} t} + A_{2} e^{s_{2} t}

$α = ω_{0}$

i (t) = (A_{2} + A_{1} t) e^{- α t}

$α < ω_{0}$

i (t) = e^{- α t} (B_{1} \cos (ω_{d} t) + B_{2} \sin (ω_{d} t))

其中，s 为特征值或自然频率 (natural frequency)；α 为奈培频率 (neper frequency)；ω₀ 为共振频率 (resonant frequency) 或无阻尼频率 (undamped natural frequency)；ω_d 为阻尼频率 (damped frequency)：

s_{1} = - α + \sqrt{α^{2} - ω_{0}^{2}}, s_{2} = - α - \sqrt{α^{2} - ω_{0}^{2}}

α = \frac{R}{2 L}, ω_{0} = \frac{1}{\sqrt{L C}}, ω_{d} = \sqrt{ω_{0}^{2} - α^{2}}

无源并联 RLC 电路

The Source-Free Parallel RLC Circuit

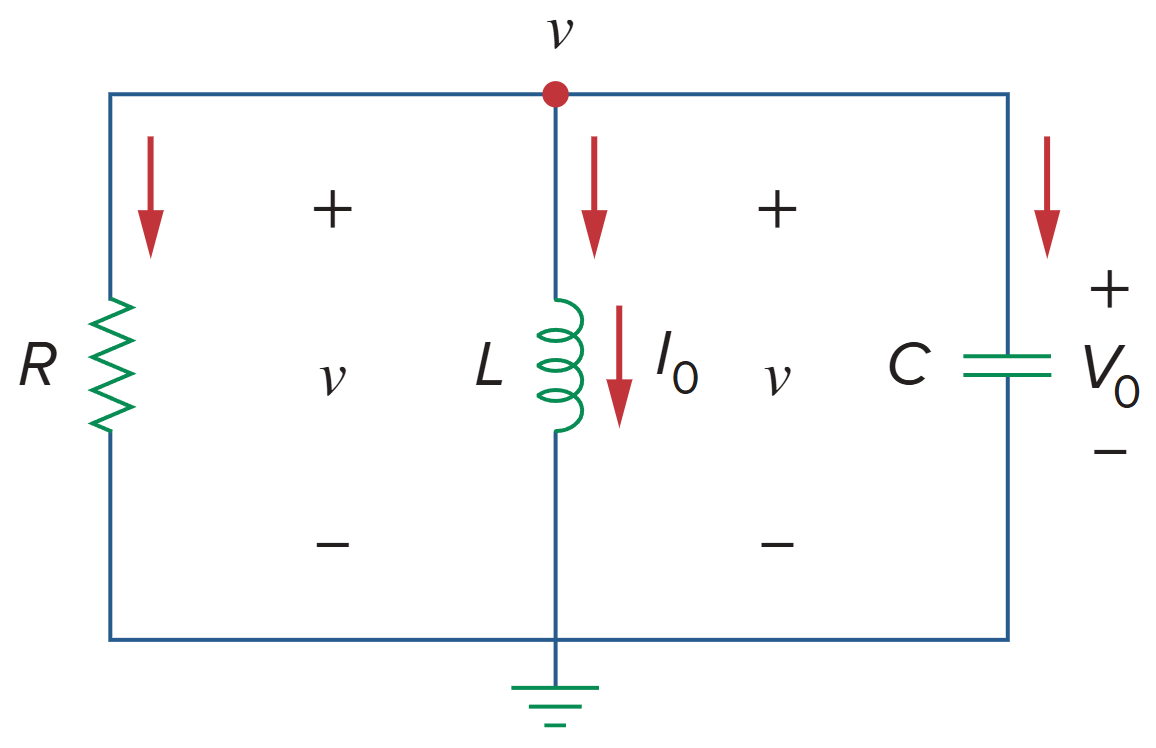
如图：

\begin{aligned} i (0) & = I_{0} = \frac{1}{L} \int_{- \infty}^{0} v (t) d t = I_{0} \\ v (0) & = V_{0} \end{aligned}

应用 KCL：

\frac{v}{R} + \frac{1}{L} \int_{- \infty}^{t} v (τ) d τ + C \frac{d v}{d t} = 0

对上式的两边求关于 $t$ 的导数，得到：

\frac{d^{2} v}{d t^{2}} + \frac{1}{R C} \frac{d v}{d t} + \frac{1}{L C} v = 0

这是一个二阶齐次线性微分方程。其初值条件为：

{\begin{aligned} v (0) & = V_{0} \\ \frac{d v}{d t} (0) & = - \frac{1}{C} (\frac{V_{0}}{R} + I_{0}) \end{aligned}

通解

$α > ω_{0}$

v (t) = A_{1} e^{s_{1} t} + A_{2} e^{s_{2} t}

$α = ω_{0}$

v (t) = (A_{1} + A_{2} t) e^{- α t}

$α < ω_{0}$

v (t) = e^{- α t} (A_{1} \cos (ω_{d} t) + A_{2} \sin (ω_{d} t))

其中，

s_{1, 2} = - α \pm \sqrt{α^{2} - ω_{0}^{2}}

α = \frac{1}{2 R C}, ω_{0} = \frac{1}{\sqrt{L C}}, ω_{d} = \sqrt{ω_{0}^{2} - α^{2}}

阶跃响应串联 RLC 电路

Step Response of a Series RLC Circuit

\begin{aligned} v (t) & = V_{s} + A_{1} e^{s_{1} t} + A_{2} e^{s_{2} t} (Overdamped) \\ v (t) & = V_{s} + (A_{1} + A_{2} t) e^{- α t} (Critically Damped) \\ v (t) & = V_{s} + (A_{1} \cos (ω_{d} t) + A_{2} \sin (ω_{d} t)) e^{- α t} (Underdamped) \end{aligned}

阶跃响应并联 RLC 电路

Step Response of a Parallel RLC Circuit

\begin{aligned} i (t) & = I_{s} + A_{1} e^{s_{1} t} + A_{2} e^{s_{2} t} (Overdamped) \\ i (t) & = I_{s} + (A_{1} + A_{2} t) e^{- α t} (Critically Damped) \\ i (t) & = I_{s} + (A_{1} \cos (ω_{d} t) + A_{2} \sin (ω_{d} t)) e^{- α t} (Underdamped) \end{aligned}

二阶电路 ​

无源串联 RLC 电路 ​

通解 ​

无源并联 RLC 电路 ​