结构分析

Structural Analysis

在线仿真模拟网站：2D-Truss Analysis

桁架

Trusses 桁héng架

https://www.youtube.com/watch?v=Hn_iozUo9m4&ab_channel=TheEfficientEngineer

基本假设

Assumptions for Design

结构中所有的节点 (joints) 都可以用销轴连接 (pinned connection) 来表示，这意味着杠件 (members) 可以在节点处自由旋转。桁架的杠件之间通常使用所谓的角撑板 (gusset plate) 刚性连接。若一个节点上所有杠件的中心线相交于一点，则可以假设这个节点是销轴连接。

The members are joined together by smooth pins.

荷载 (loading) 只作用在桁架的节点处。即没有荷载作用在一个杠件的中间。因为每个杠件必须处于平衡状态，所以作用在杠件两端的力必须相等且相反。每个杠件不是受到拉伸 (Tension) 就是受到压缩 (Compression)。

All loading are applied at the joints.

简单桁架

Simple Truss

节点法

The Method of Joints

零力构件 / 零杠

Zero-Force Members

If only two non-collinear members form a truss joint and no external load or support reaction is applied to the joint, the two members must be zero-force memebers.

If three members form a truss joint for which two of the members are collinear, the third member is a zero-force member provided no external force or support reaction has a component that acts along this member.

截面法

The Method of Sections

* 空间桁架

Space Trusses

在本书中属于非重点内容。

A space truss consists of members joined together at their ends to form a stable three-dimensional structure. The simplest form of a space truss is a tetrahedron, constructed by connecting six members together.

框架与机械

Frames and Machines

综合题目

补充

2D-Truss Analysis

在线二维结构分析工具：2D-Truss calculator - online

示例

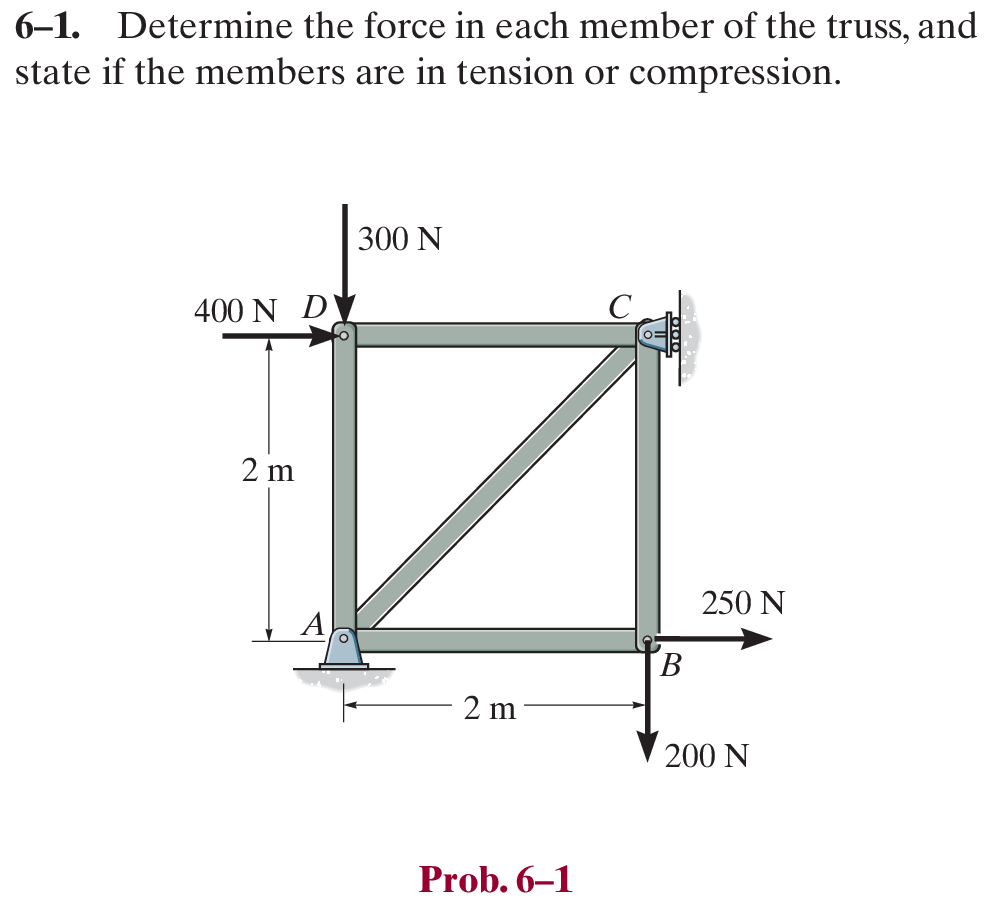
Prob_6_1

Python 解题

Python

# ===============================================================================
# 6-1. 桁架结构分析 - 节点法求解 (优化注释版本)
# ===============================================================================
# 
# 问题描述：
# 假设构件 AB, BC, CD, DA, AC 分别承受轴向力 F1, F2, F3, F4, F5
# 力的符号约定：正值为拉力，负值为压力
# 
# 求解方法：使用节点法（Method of Joints）
# 基本原理：对每个节点建立力平衡方程（ΣFx = 0, ΣFy = 0）
# ===============================================================================

import sympy as sp

# ===============================================================================
# 第一步：分析节点 B 的力平衡
# ===============================================================================
# 节点 B 受到外载荷：水平向右 250N，竖直向下 200N
F_load_B = sp.Matrix([250, -200])  # [Fx, Fy]，y轴向上为正

# 计算节点 B 与构件 BA 和 BC 的连接力
# 注意：这里使用点积投影来分解外载荷
F_BA = - F_load_B.dot(sp.Matrix([1, 0])) * sp.Matrix([1, 0])  # BA方向力（水平）
F_BC = - F_load_B.dot(sp.Matrix([0, 1])) * sp.Matrix([0, 1])  # BC方向力（竖直）

# 计算构件轴向力的大小（注意方向）
F1 = F_BA.dot(sp.Matrix([-1, 0]))  # AB构件轴向力（从A指向B为正）
F2 = F_BC.dot(sp.Matrix([0, 1]))   # BC构件轴向力（从B指向C为正）

# ===============================================================================
# 第二步：分析节点 D 的力平衡
# ===============================================================================
# 节点 D 受到外载荷：水平向右 400N，竖直向下 300N
F_load_D = sp.Matrix([400, -300])  # [Fx, Fy]

# 计算节点 D 与构件 DC 和 DA 的连接力
F_DC = - F_load_D.dot(sp.Matrix([1, 0])) * sp.Matrix([1, 0])  # DC方向力（水平）
F_DA = - F_load_D.dot(sp.Matrix([0, 1])) * sp.Matrix([0, 1])  # DA方向力（竖直）

# 计算构件轴向力的大小
F3 = F_DC.dot(sp.Matrix([1, 0]))   # CD构件轴向力（从C指向D为正）
F4 = F_DA.dot(sp.Matrix([0, -1]))  # DA构件轴向力（从D指向A为正）

# ===============================================================================
# 第三步：分析节点 C 的力平衡
# ===============================================================================
# 节点 C 连接构件：CB, CD, CA 以及可能的支反力
F_CB = - F_BC  # CB力等于BC力的反向
F_CD = - F_DC  # CD力等于DC力的反向

# 定义未知量：AC构件的轴向力大小和C点的支反力
F_CA_magnitude, C_x = sp.symbols('F_CA_magnitude, C_x', real=True)
C = sp.Matrix([C_x, 0])  # C点支反力（仅水平方向）

# AC构件与水平方向成-135°角（从A指向C）
angle_AC = sp.rad(-135)  # 转换为弧度
F_CA = sp.Matrix([
    F_CA_magnitude * sp.cos(angle_AC),  # AC力的x分量
    F_CA_magnitude * sp.sin(angle_AC)   # AC力的y分量
])

# 建立节点C的力平衡方程
eqs = [
    sp.Eq(F_CB[0] + F_CD[0] + C[0] + F_CA[0], 0),  # x方向平衡：ΣFx = 0
    sp.Eq(F_CB[1] + F_CD[1] + F_CA[1], 0)          # y方向平衡：ΣFy = 0
]

# ===============================================================================
# 第四步：分析节点 A 的力平衡
# ===============================================================================
# 节点 A 连接构件：AB, AD, AC 以及支反力
A_x, A_y = sp.symbols('A_x A_y', real=True)  # A点的支反力分量
F_AB = - F_BA  # AB力等于BA力的反向
F_AD = - F_DA  # AD力等于DA力的反向
F_AC = - F_CA  # AC力等于CA力的反向
A = sp.Matrix([A_x, A_y])  # A点支反力向量

# 建立节点A的力平衡方程，并添加到方程组中
eqs.append(sp.Eq(F_AB[0] + F_AD[0] + A[0] + F_AC[0], 0))  # x方向平衡
eqs.append(sp.Eq(F_AB[1] + F_AD[1] + A[1] + F_AC[1], 0))  # y方向平衡

# ===============================================================================
# 第五步：求解联立方程组
# ===============================================================================
# 同时求解所有未知量：AC构件轴向力、支反力等
sol = sp.solve(eqs, [F_CA_magnitude, C_x, A_x, A_y], dict=True)

# 计算AC构件的轴向力（沿构件方向的分量）
unit_vector_AC = sp.Matrix([sp.cos(angle_AC), sp.sin(angle_AC)])
F5 = F_CA.subs(sol[0]).dot(unit_vector_AC)

# ===============================================================================
# 结果输出和解释
# ===============================================================================
print("=" * 70)
print("桁架结构分析结果（节点法）")
print("=" * 70)
print("假设构件 AB, BC, CD, DA, AC 分别承受轴向力 F1, F2, F3, F4, F5")
print("符号约定：正值表示拉力，负值表示压力")
print("-" * 70)

member_names = ["AB", "BC", "CD", "DA", "AC"]

for i, (member, force) in enumerate(zip(member_names, [F1, F2, F3, F4, F5]), start=1):
    force_type = "拉力" if float(force) > 0 else "压力"
    print(f"F{i} ({member}): {force:.2f} N ({force_type})")

print("=" * 70)

输出结果：

txt

======================================================================
桁架结构分析结果（节点法）
======================================================================
假设构件 AB, BC, CD, DA, AC 分别承受轴向力 F1, F2, F3, F4, F5
符号约定：正值表示拉力，负值表示压力
----------------------------------------------------------------------
F1 (AB): 250.00 N (拉力)
F2 (BC): 200.00 N (拉力)
F3 (CD): -400.00 N (压力)
F4 (DA): -300.00 N (压力)
F5 (AC): -282.84 N (压力)
======================================================================

2D-Truss Analysis 解题

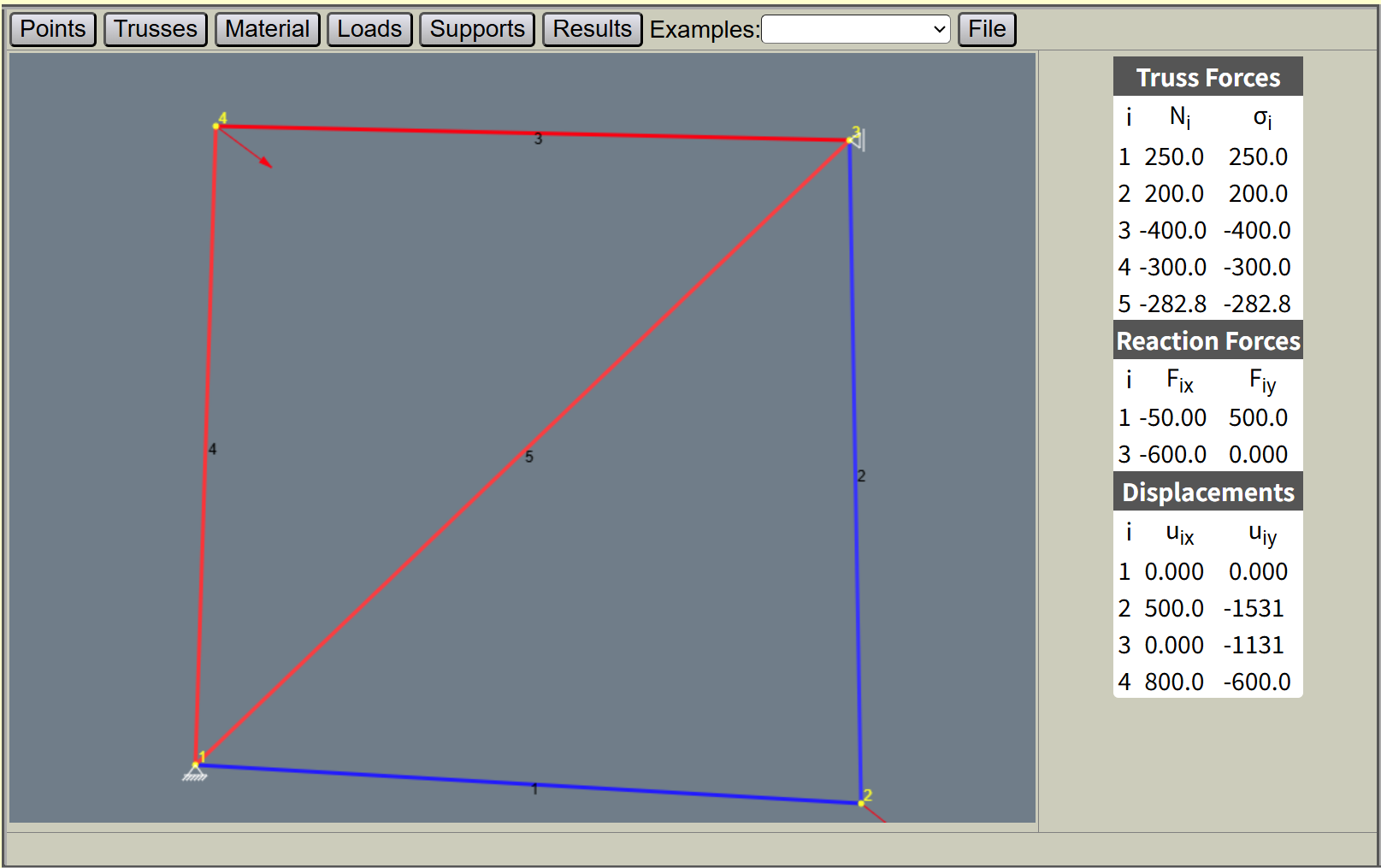
Prob_6_33

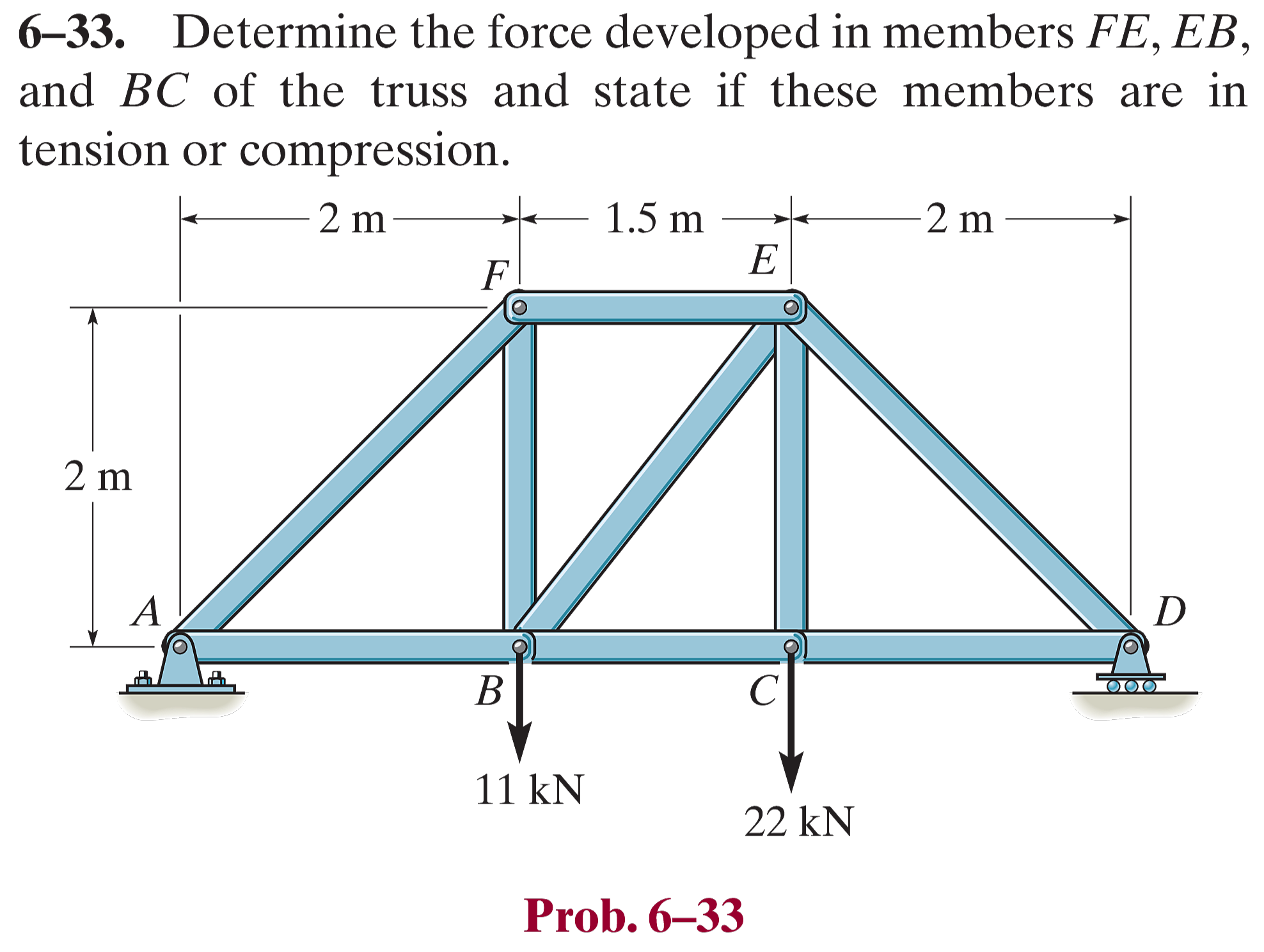
受力分析图

Python 解题

Python

# ===============================================================================
# 6-33. 桁架结构分析 - 截面法求解 (优化注释版本)
# ===============================================================================
# 
# 问题描述：
# 使用截面法（Method of Sections）分析桁架结构中特定构件的内力
# 
# 求解方法：截面法
# 基本原理：通过假想切开桁架的某个截面，对截面一侧的部分建立平衡方程
# 优势：可以直接求出感兴趣构件的内力，无需逐个节点分析
# ===============================================================================

import sympy as sp

# ===============================================================================
# 步骤一：定义桁架几何结构
# ===============================================================================
# 定义桁架各节点的坐标位置 (单位：m)
point_A = sp.Matrix([0, 0])      # 左支座点A
point_B = sp.Matrix([2, 0])      # 节点B  
point_C = sp.Matrix([3.5, 0])    # 节点C
point_D = sp.Matrix([5.5, 0])    # 右支座点D
point_E = sp.Matrix([3.5, 2])    # 上弦节点E
point_F = sp.Matrix([2, 2])      # 上弦节点F

# 定义外载荷 (单位：N，向下为负)
G_B = sp.Matrix([0, -11e3])  # 节点B处的垂直载荷：11 kN向下
G_C = sp.Matrix([0, -22e3])  # 节点C处的垂直载荷：22 kN向下

# ===============================================================================
# 步骤二：计算支座反力
# ===============================================================================
# 定义支座反力的未知量
A_y = sp.symbols('A_y', real=True)  # A点竖直反力
D_y = sp.symbols('D_y', real=True)  # D点竖直反力
A = sp.Matrix([0, A_y])  # A点反力向量（水平反力为0，因为无水平外力）
D = sp.Matrix([0, D_y])  # D点反力向量

# 计算位置向量（从A点到各力作用点）
r_AB = point_B - point_A  # A到B的位置向量
r_AC = point_C - point_A  # A到C的位置向量  
r_AD = point_D - point_A  # A到D的位置向量

# 定义二维向量叉积函数（计算力矩标量值）
def cross2d(a, b):
    """计算二维向量的叉积标量值 a × b = a_x*b_y - a_y*b_x"""
    return a[0]*b[1] - a[1]*b[0]

# 建立平衡方程
# 1. 对A点的力矩平衡：ΣM_A = 0
M_A = cross2d(r_AB, G_B) + cross2d(r_AC, G_C) + cross2d(r_AD, D)

# 2. 竖直方向力平衡：ΣF_y = 0
force_balance_y = A_y + G_B[1] + G_C[1] + D_y

# 求解支座反力
support_eqs = [
    sp.Eq(M_A, 0),                    # 力矩平衡方程
    sp.Eq(force_balance_y, 0)         # 竖直力平衡方程
]

support_sol = sp.solve(support_eqs, [A_y, D_y], dict=True)
A_y_value = support_sol[0][A_y]
D_y_value = support_sol[0][D_y]

# 更新支座反力向量
A = sp.Matrix([0, A_y_value])
D = sp.Matrix([0, D_y_value])

print(f"支座反力计算结果:")
print(f"A点竖直反力: {A_y_value/1000:.1f} kN ({'向上' if A_y_value > 0 else '向下'})")
print(f"D点竖直反力: {D_y_value/1000:.1f} kN ({'向上' if D_y_value > 0 else '向下'})")
print(f"验证：总竖直力 = {(A_y_value + D_y_value + G_B[1] + G_C[1])/1000:.1f} kN (应为0)")
print("-" * 70)

# 清理临时变量
del support_eqs, support_sol

# ===============================================================================
# 步骤三：使用截面法分析构件内力
# ===============================================================================
# 定义待求构件的轴向力大小（未知量）
F_BC_magnitude = sp.symbols('F_BC_magnitude', real=True)  # BC构件轴向力
F_BE_magnitude = sp.symbols('F_BE_magnitude', real=True)  # BE构件轴向力  
F_EF_magnitude = sp.symbols('F_EF_magnitude', real=True)  # EF构件轴向力

# ===============================================================================
# 方法一：分析左侧截面
# ===============================================================================

# 计算构件方向向量和单位向量
r_BC = point_C - point_B  # BC构件方向向量
r_BE = point_E - point_B  # BE构件方向向量
r_FE = point_E - point_F  # FE构件方向向量（注意：从F指向E）

u_BC = r_BC / r_BC.norm()  # BC构件单位向量
u_BE = r_BE / r_BE.norm()  # BE构件单位向量
u_FE = r_FE / r_FE.norm()  # FE构件单位向量

# 构件内力向量（轴向力 × 单位向量）
F_BC = F_BC_magnitude * u_BC  # BC构件内力向量
F_BE = F_BE_magnitude * u_BE  # BE构件内力向量
F_FE = F_EF_magnitude * u_FE  # FE构件内力向量

# 建立左侧截面的平衡方程
# 选择B点作为力矩平衡点（可消除通过B点的力的力矩）
r_BF = point_F - point_B  # B到F的位置向量
r_BA = point_A - point_B  # B到A的位置向量

# 对B点的力矩平衡：ΣM_B = 0
M_B = cross2d(r_BF, F_FE) + cross2d(r_BA, A)

# 力平衡方程：ΣF_x = 0, ΣF_y = 0
force_x = F_BC[0] + F_BE[0] + F_FE[0] + A[0] + G_B[0]
force_y = F_BC[1] + F_BE[1] + F_FE[1] + A[1] + G_B[1]

# 建立方程组并求解
left_section_eqs = [
    sp.Eq(M_B, 0),      # 力矩平衡
    sp.Eq(force_x, 0),  # x方向力平衡
    sp.Eq(force_y, 0)   # y方向力平衡
]

left_section_sol = sp.solve(left_section_eqs, [F_BC_magnitude, F_BE_magnitude, F_EF_magnitude], dict=True)

print("左侧截面分析结果:")
for member, magnitude in [("BC", F_BC_magnitude), ("BE", F_BE_magnitude), ("EF", F_EF_magnitude)]:
    force_value = left_section_sol[0][magnitude]
    force_type = "拉力" if force_value > 0 else "压力"
    print(f"构件{member}: {force_value/1000:.2f} kN ({force_type})")

# 清理临时变量
del left_section_eqs, left_section_sol

# ===============================================================================
# 方法二：分析右侧截面（验证）
# ===============================================================================

# 注意：右侧截面中构件方向需要重新定义（指向截面内部）
r_CB = point_B - point_C  # CB构件方向向量（从C指向B）
r_EB = point_B - point_E  # EB构件方向向量（从E指向B）
r_EF = point_F - point_E  # EF构件方向向量（从E指向F）

u_CB = r_CB / r_CB.norm()  # CB构件单位向量
u_EB = r_EB / r_EB.norm()  # EB构件单位向量
u_EF = r_EF / r_EF.norm()  # EF构件单位向量

# 构件内力向量（注意：轴向力大小相同，但方向需要调整）
F_CB = F_BC_magnitude * u_CB  # CB构件内力向量
F_EB = F_BE_magnitude * u_EB  # EB构件内力向量
F_EF = F_EF_magnitude * u_EF  # EF构件内力向量

# 建立右侧截面的平衡方程
# 选择C点作为力矩平衡点
r_CD = point_D - point_C  # C到D的位置向量
r_CE = point_E - point_C  # C到E的位置向量

# 对C点的力矩平衡：ΣM_C = 0
M_C = cross2d(r_CD, D) + cross2d(r_CE, F_EB) + cross2d(r_CE, F_EF)

# 力平衡方程：ΣF_x = 0, ΣF_y = 0
force_x_right = F_CB[0] + F_EB[0] + F_EF[0] + D[0] + G_C[0]
force_y_right = F_CB[1] + F_EB[1] + F_EF[1] + D[1] + G_C[1]

# 建立方程组并求解
right_section_eqs = [
    sp.Eq(M_C, 0),              # 力矩平衡
    sp.Eq(force_x_right, 0),    # x方向力平衡
    sp.Eq(force_y_right, 0)     # y方向力平衡
]

right_section_sol = sp.solve(right_section_eqs, [F_BC_magnitude, F_BE_magnitude, F_EF_magnitude], dict=True)

print("右侧截面分析结果:")
for member, magnitude in [("BC", F_BC_magnitude), ("BE", F_BE_magnitude), ("EF", F_EF_magnitude)]:
    force_value = right_section_sol[0][magnitude]
    force_type = "拉力" if force_value > 0 else "压力"
    print(f"构件{member}: {force_value/1000:.2f} kN ({force_type})")

# ===============================================================================
# 结果验证和总结
# ===============================================================================
print("\n" + "=" * 70)
print("截面法分析总结")
print("=" * 70)
print("验证：左侧截面和右侧截面的分析结果应该完全一致")
print("这证明了截面法的正确性和力学平衡的一致性")
print()
print("最终结果：")
for member, magnitude in [("BC", F_BC_magnitude), ("BE", F_BE_magnitude), ("EF", F_EF_magnitude)]:
    force_value = right_section_sol[0][magnitude]
    force_type = "拉力" if force_value > 0 else "压力"
    print(f"构件{member}: {abs(force_value)/1000:.2f} kN ({force_type})")

print("=" * 70)

输出结果：

txt

支座反力计算结果:
A点竖直反力: 15.0 kN (向上)
D点竖直反力: 18.0 kN (向上)
验证：总竖直力 = 0.0 kN (应为0)
----------------------------------------------------------------------
左侧截面分析结果:
构件BC: 18.00 kN (拉力)
构件BE: -5.00 kN (压力)
构件EF: -15.00 kN (压力)
右侧截面分析结果:
构件BC: 18.00 kN (拉力)
构件BE: -5.00 kN (压力)
构件EF: -15.00 kN (压力)

======================================================================
截面法分析总结
======================================================================
验证：左侧截面和右侧截面的分析结果应该完全一致
这证明了截面法的正确性和力学平衡的一致性

最终结果：
构件BC: 18.00 kN (拉力)
构件BE: 5.00 kN (压力)
构件EF: 15.00 kN (压力)
======================================================================

2D-Truss Analysis 解题

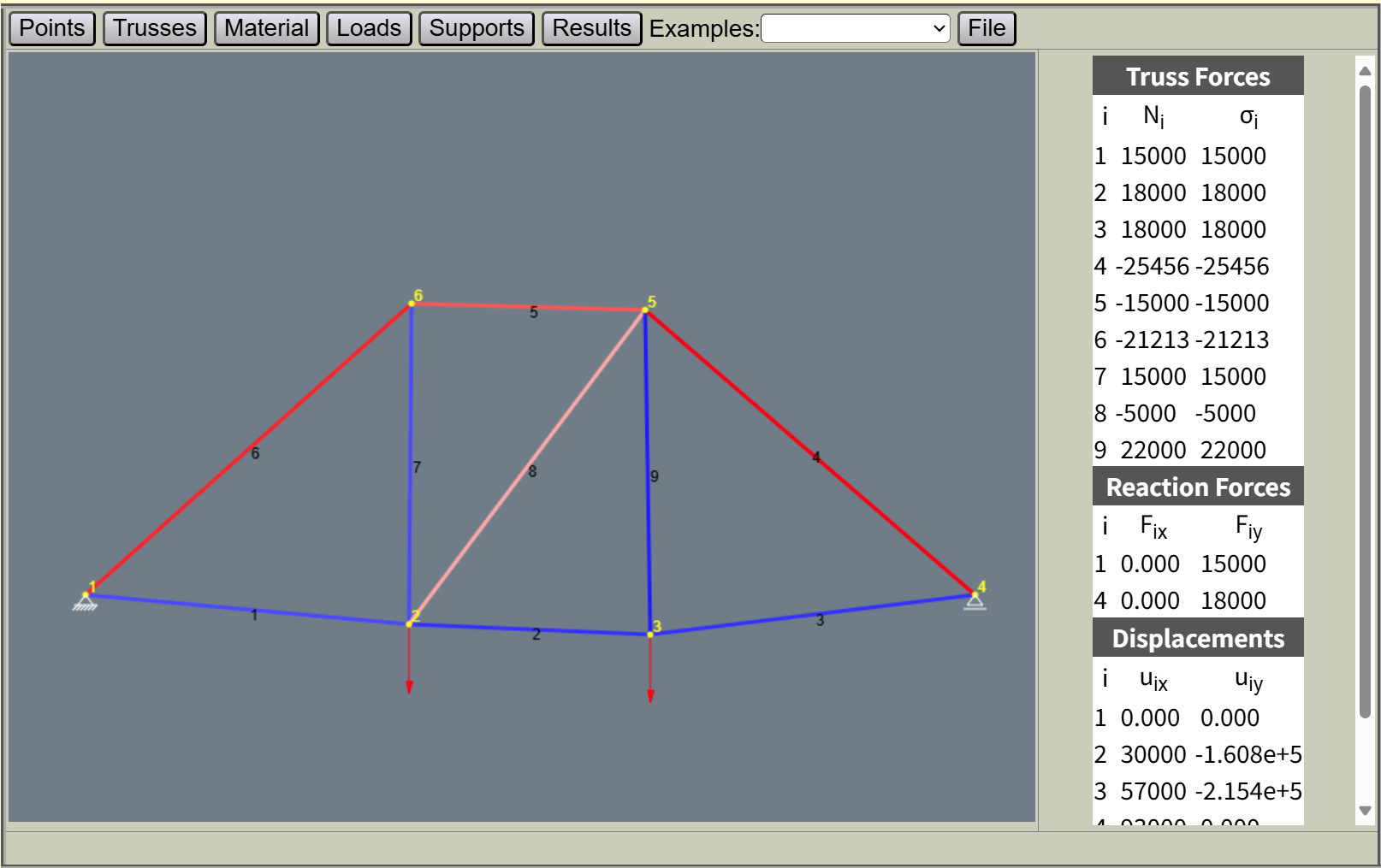
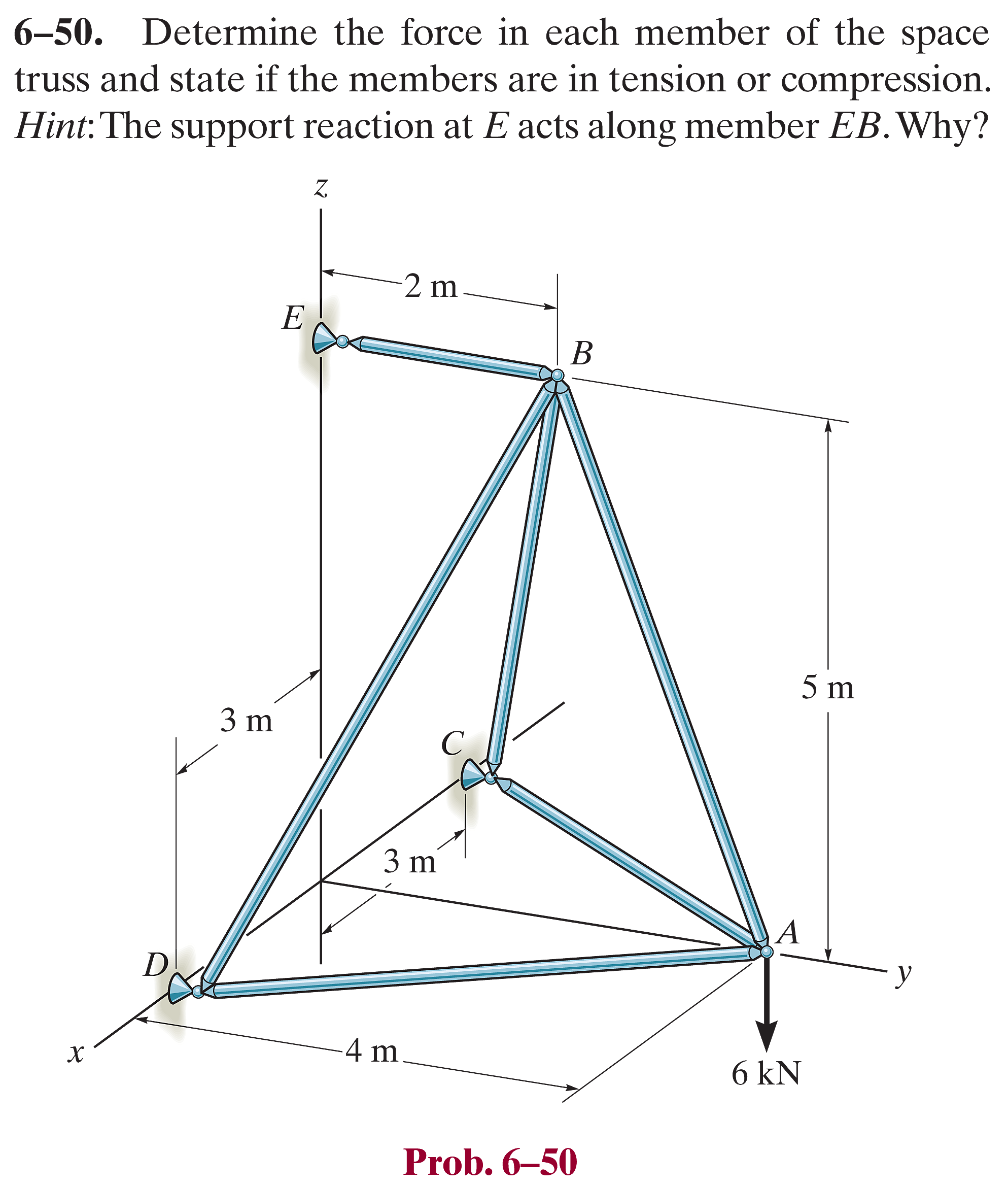
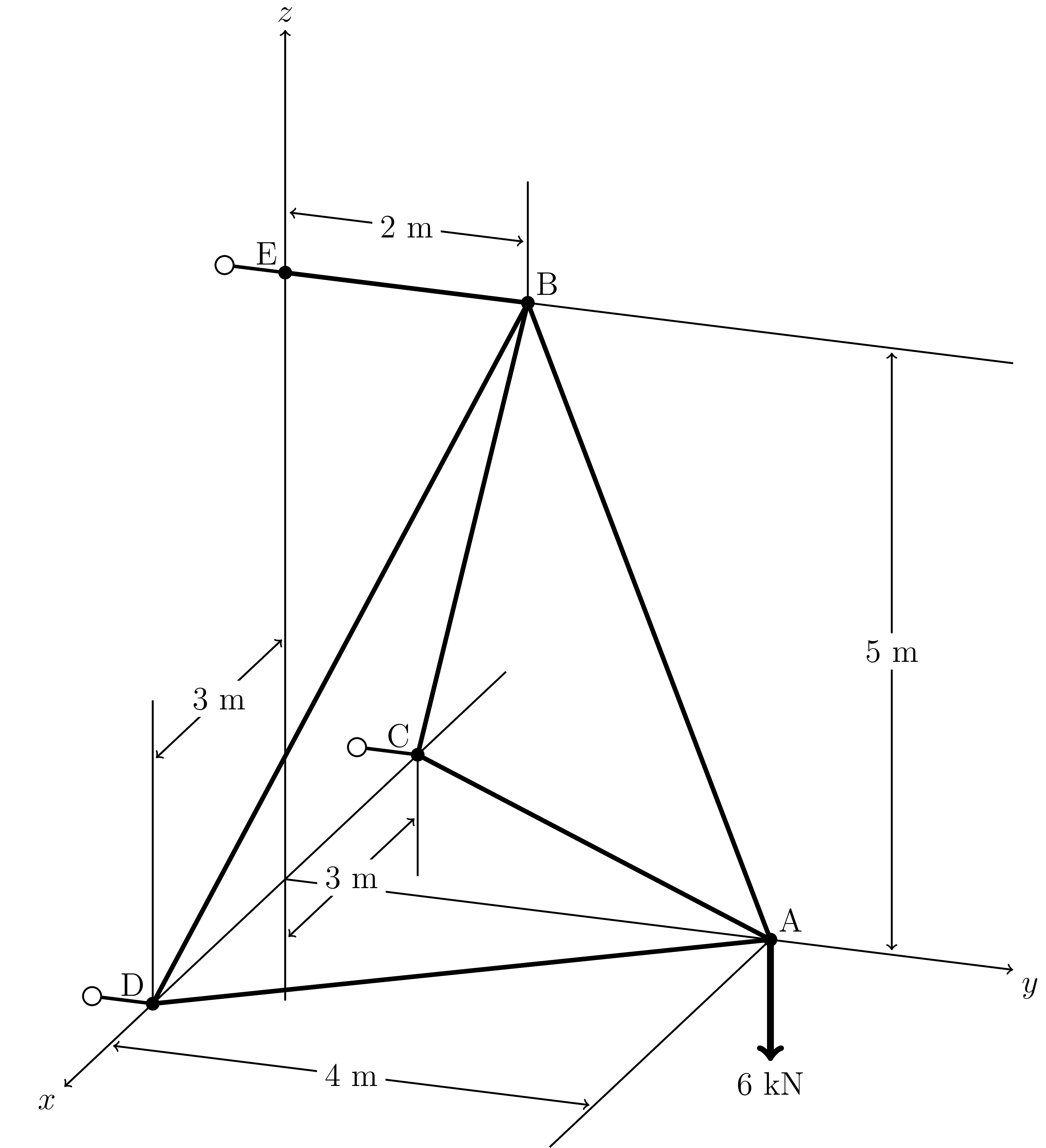
Prob_6_50

TikZ 作图

Python 解题

Python

import sympy as sp

point_A = sp.Matrix([0, 4, 0])
point_B = sp.Matrix([0, 2, 5])
point_C = sp.Matrix([-3, 0, 0])
point_D = sp.Matrix([3, 0, 0])
point_E = sp.Matrix([0, 0, 5])

G_A = sp.Matrix([0, 0, -6e3]) 

# 节点法

## 节点A
F_AB_magnitude = sp.symbols('F_AB', real=True)
F_AC_magnitude = sp.symbols('F_AC', real=True)
F_AD_magnitude = sp.symbols('F_AD', real=True)
u_AB = (point_B - point_A).normalized()
u_AC = (point_C - point_A).normalized()
u_AD = (point_D - point_A).normalized()
F_AB = F_AB_magnitude * u_AB
F_AC = F_AC_magnitude * u_AC
F_AD = F_AD_magnitude * u_AD

eqs = [
    sp.Eq(F_AB[0] + F_AC[0] + F_AD[0] + G_A[0], 0),
    sp.Eq(F_AB[1] + F_AC[1] + F_AD[1] + G_A[1], 0),
    sp.Eq(F_AB[2] + F_AC[2] + F_AD[2] + G_A[2], 0)
]

## 节点B
F_BA = - F_AB
F_BC_magnitude = sp.symbols('F_BC', real=True)
F_BD_magnitude = sp.symbols('F_BD', real=True)
F_BE_magnitude = sp.symbols('F_BE', real=True)
u_BC = (point_C - point_B).normalized()
u_BD = (point_D - point_B).normalized()
u_BE = (point_E - point_B).normalized()
F_BC = F_BC_magnitude * u_BC
F_BD = F_BD_magnitude * u_BD
F_BE = F_BE_magnitude * u_BE

eqs.append(sp.Eq(F_BA[0] + F_BC[0] + F_BD[0] + F_BE[0], 0))
eqs.append(sp.Eq(F_BA[1] + F_BC[1] + F_BD[1] + F_BE[1], 0))
eqs.append(sp.Eq(F_BA[2] + F_BC[2] + F_BD[2] + F_BE[2], 0))

sol = sp.solve(eqs, [F_AB_magnitude, 
                     F_AC_magnitude, 
                     F_AD_magnitude, 
                     F_BC_magnitude,
                     F_BD_magnitude,
                     F_BE_magnitude,
                     ], dict=True)

# 各个杠杆的受力情况
print("=== 各个杠杆的受力情况 ===")
F_AB_val = sol[0][F_AB_magnitude]
F_AC_val = sol[0][F_AC_magnitude]
F_AD_val = sol[0][F_AD_magnitude]
F_BC_val = sol[0][F_BC_magnitude]
F_BD_val = sol[0][F_BD_magnitude]
F_BE_val = sol[0][F_BE_magnitude]

def force_type(force_value):
    if abs(force_value) < 1e-6:  # 接近零的值
        return "零杆"
    elif force_value > 0:
        return "拉力"
    else:
        return "压力"

print(f"F_AB = {F_AB_val:.3g} N ({force_type(F_AB_val)})")
print(f"F_AC = {F_AC_val:.3g} N ({force_type(F_AC_val)})")
print(f"F_AD = {F_AD_val:.3g} N ({force_type(F_AD_val)})")
print(f"F_BC = {F_BC_val:.3g} N ({force_type(F_BC_val)})")
print(f"F_BD = {F_BD_val:.3g} N ({force_type(F_BD_val)})")
print(f"F_BE = {F_BE_val:.3g} N ({force_type(F_BE_val)})")

输出结果：

txt

=== 各个杠杆的受力情况 ===
F_AB = 6.46e+3 N (拉力)
F_AC = -1.50e+3 N (压力)
F_AD = -1.50e+3 N (压力)
F_BC = -3.70e+3 N (压力)
F_BD = -3.70e+3 N (压力)
F_BE = 4.80e+3 N (拉力)

Prob_F6_24

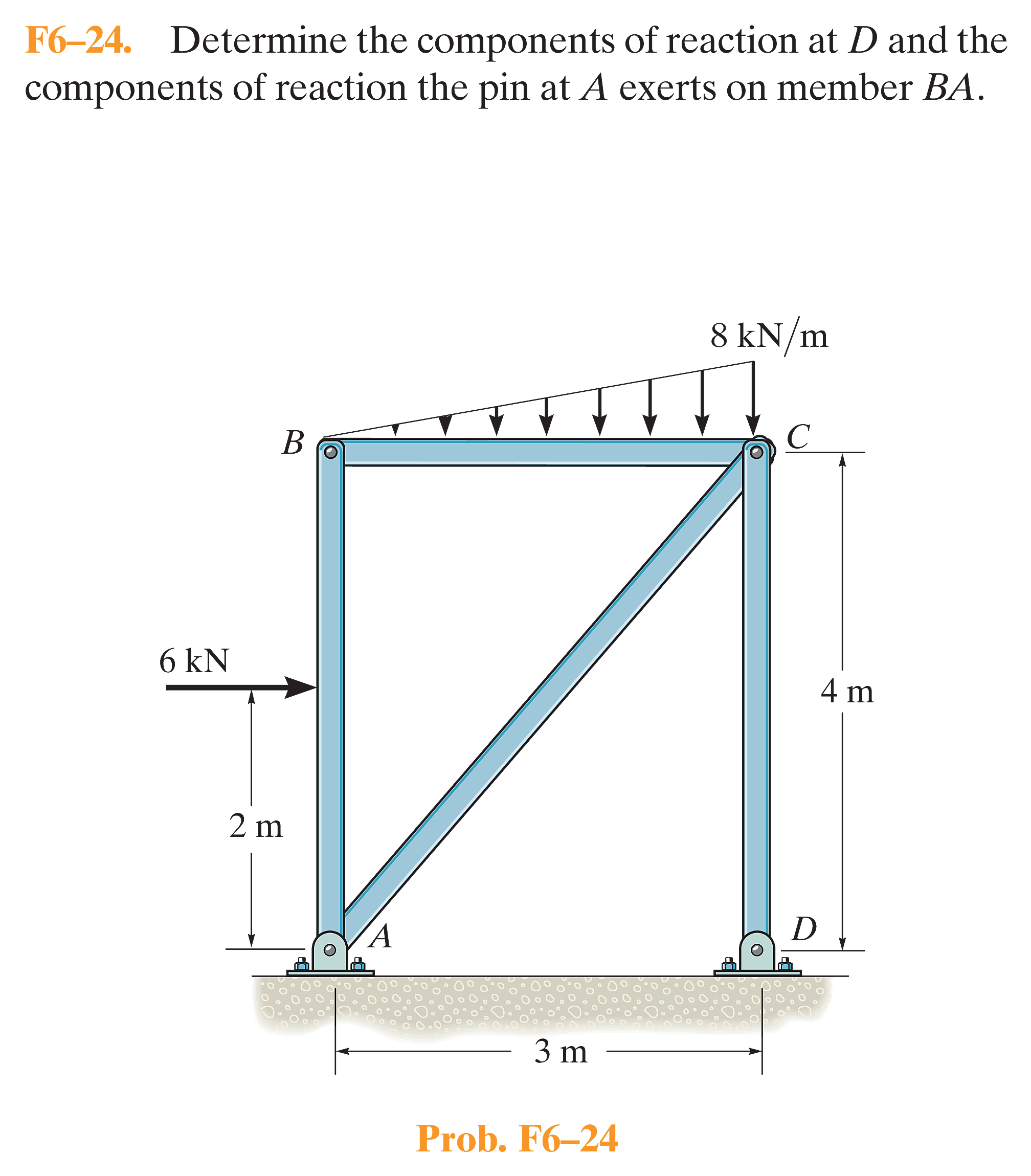
受力分析图

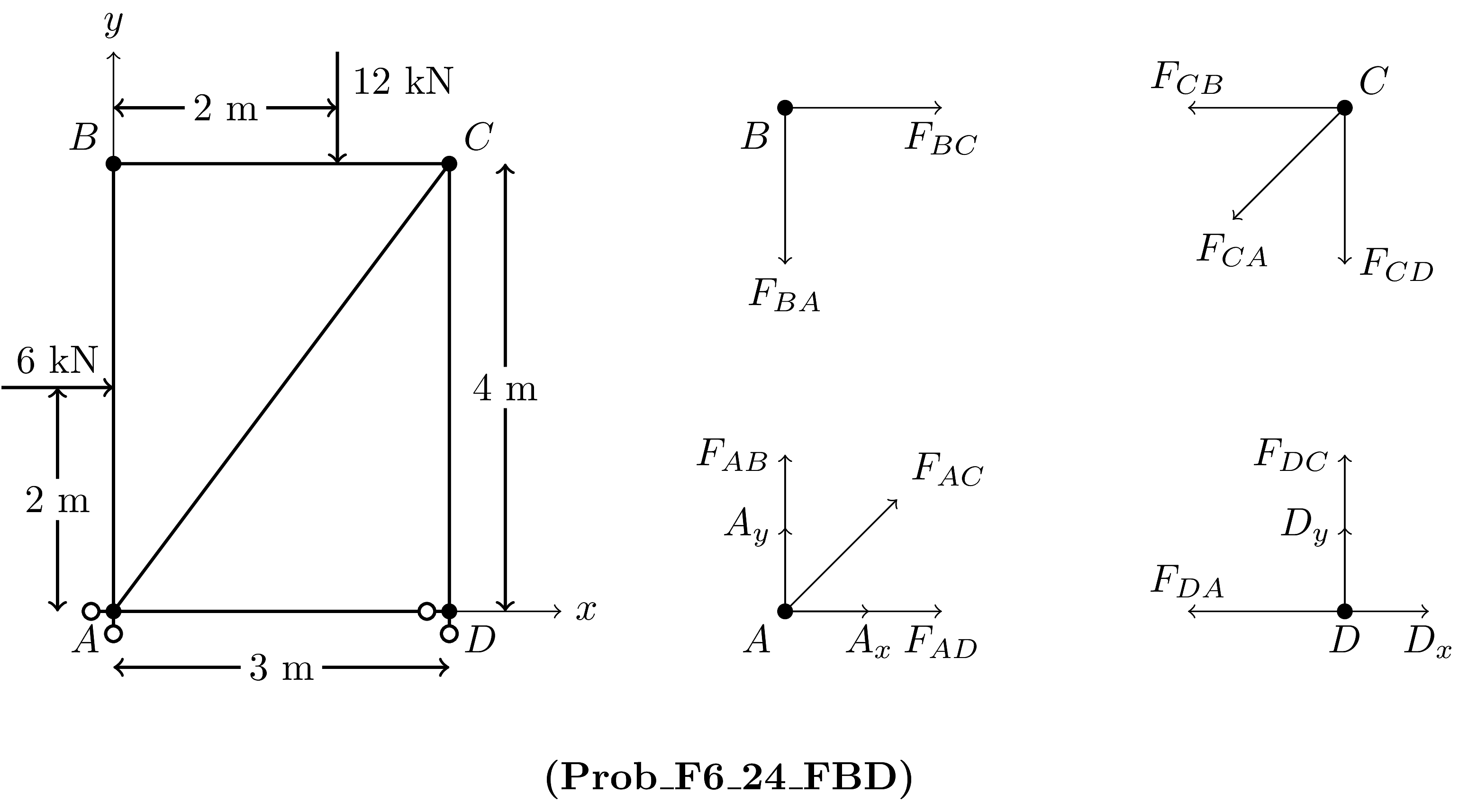
Python 解题

Python

import sympy as sp

point_A = sp.Matrix([0, 0])
point_B = sp.Matrix([0, 4])
point_C = sp.Matrix([3, 4])
point_D = sp.Matrix([3, 0])

F_1 = sp.Matrix([6e3, 0])
F_2 = sp.Matrix([0, -12e3])
position_1 = sp.Matrix([0, 2])
position_2 = sp.Matrix([2, 4])

A_x, A_y = sp.symbols('A_x A_y', real=True)
D_x, D_y = sp.symbols('D_x D_y', real=True)

def cross_2D(r, F):
    return r[0]*F[1] - r[1]*F[0]

# M_C
F_AB_magnitude = sp.symbols('F_AB', real=True)
F_BA = F_AB_magnitude * sp.Matrix([0, -1])
r_CB = point_B - point_C
r_C2 = position_2 - point_C
M_C = cross_2D(r_CB, F_BA) + cross_2D(r_C2, F_2)
sol = sp.solve(sp.Eq(M_C, 0), F_AB_magnitude, dict=True)[0]
F_AB_magnitude = sol[F_AB_magnitude]
F_BA = F_AB_magnitude * sp.Matrix([0, -1])
F_AB = -F_BA
sol = sp.solve(sp.Eq(sp.Matrix([0, A_y]) + F_AB, sp.Matrix([0, 0])), A_y, dict=True)[0]
A_y = sol[A_y]

# M_B
r_BA = point_A - point_B
r_B1 = position_1 - point_B
M_B = cross_2D(r_B1, F_1) + cross_2D(r_BA, sp.Matrix([A_x, 0]))
sol = sp.solve(sp.Eq(M_B, 0), A_x, dict=True)[0]
A_x = sol[A_x]

# M_A
r_A1 = position_1 - point_A
r_A2 = position_2 - point_A
r_AD = point_D - point_A
M_A = cross_2D(r_A1, F_1) + cross_2D(r_A2, F_2) + cross_2D(r_AD, sp.Matrix([0, D_y]))
sol = sp.solve(sp.Eq(M_A, 0), D_y, dict=True)[0]
D_y = sol[D_y]

# M_C
D_x = 0

print(f"A_x = {A_x/1e3:.2f} kN")
print(f"A_y = {A_y/1e3:.2f} kN")
print(f"D_x = {D_x/1e3:.2f} kN")
print(f"D_y = {D_y/1e3:.2f} kN")

输出：

txt

A_x = -3.00 kN
A_y = 4.00 kN
D_x = 0.00 kN
D_y = 12.00 kN

结构分析 ​

桁架 ​

基本假设 ​

简单桁架 ​

节点法 ​

零力构件 / 零杠 ​

截面法 ​

* 空间桁架 ​

框架与机械 ​

补充 ​

2D-Truss Analysis ​

示例 ​

Prob_6_1 ​

Prob_6_33 ​

Prob_6_50 ​

Prob_F6_24 ​

结构分析

桁架

基本假设

简单桁架

节点法

零力构件 / 零杠

截面法

* 空间桁架

框架与机械

补充

2D-Truss Analysis

示例

Prob_6_1

Prob_6_33

Prob_6_50

Prob_F6_24