三相电路

Three-Phase Circuits

在电力系统中，除非另有说明，本文中的电压和电流均以有效值 (rms) 值表示，这是一个普遍的惯例。

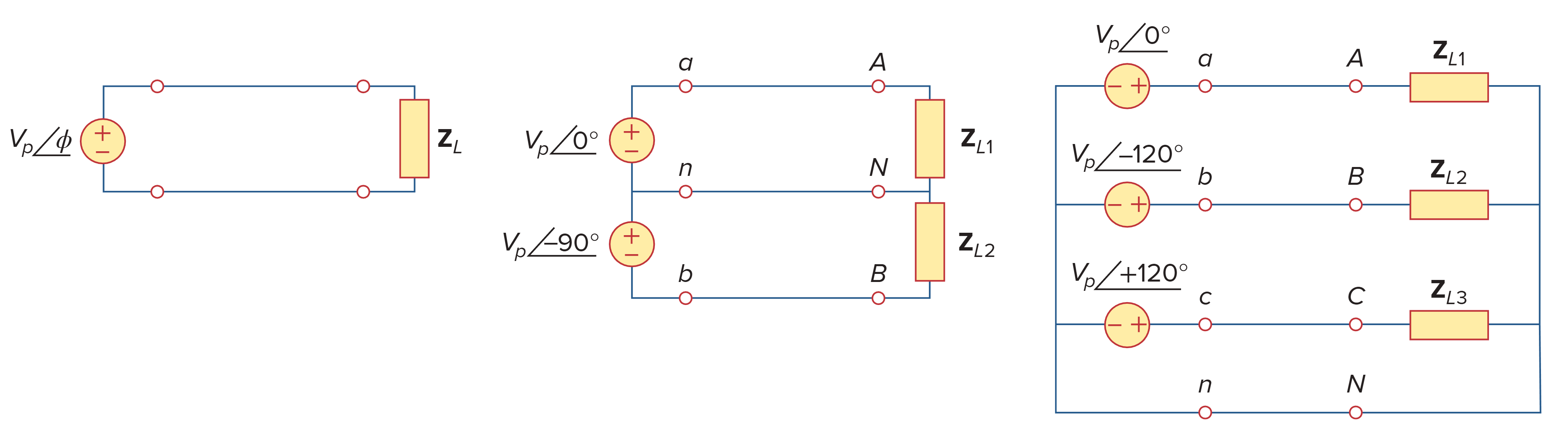
平衡三相电压

Balanced Phase Voltages

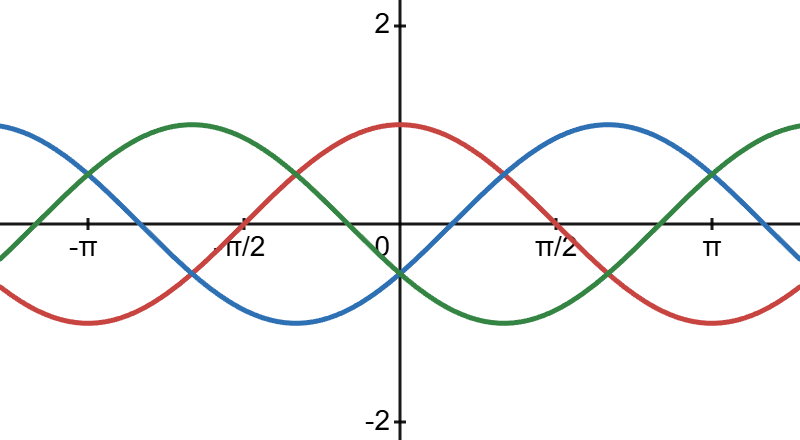
Balanced phase voltages are equal in magnitude and are out of phase with each other by 120°.

The phase sequence is the time order in which the voltages pass through their respective maximum values.

除非另有说明，本文中默认采用 positive sequence 的相序（顺时针方向）。

$$\begin{array}{rl}& {\mathbf{V}}_{an}+{\mathbf{V}}_{bn}+{\mathbf{V}}_{cn}=0\\ & |{\mathbf{V}}_{an}|=|{\mathbf{V}}_{bn}|=|{\mathbf{V}}_{cn}|=V_p\\ & {\mathbf{V}}_{an}=V_p\mathrm{\angle }0\mathrm{°}\\ & {\mathbf{V}}_{bn}=V_p\mathrm{\angle }-120\mathrm{°}\\ & {\mathbf{V}}_{cn}=V_p\mathrm{\angle }-240\mathrm{°}=V_p\mathrm{\angle }120\mathrm{°}\end{array}$$

平衡负载

Balanced Load

A balanced load is one in which the phase impedances are equal in magnitude and in phase.

$$\begin{array}{rl}& {\mathbf{Z}}_1={\mathbf{Z}}_2={\mathbf{Z}}_3={\mathbf{Z}}_Y\\ & {\mathbf{Z}}_a={\mathbf{Z}}_b={\mathbf{Z}}_c={\mathbf{Z}}_{\mathrm{\Delta }}\\ & {\mathbf{Z}}_{\mathrm{\Delta }}=3{\mathbf{Z}}_Y\\ & {\mathbf{Z}}_Y=\frac{1}{3}{\mathbf{Z}}_{\mathrm{\Delta }}\end{array}$$

平衡连接

Y-Y

Balanced Wye-Wye Connection

A balanced Y-Y system is a three-phase system with a balanced Y-connected source and a balanced Y-connected load.

$$Z_Y=Z_s+Z_l+Z_L$$

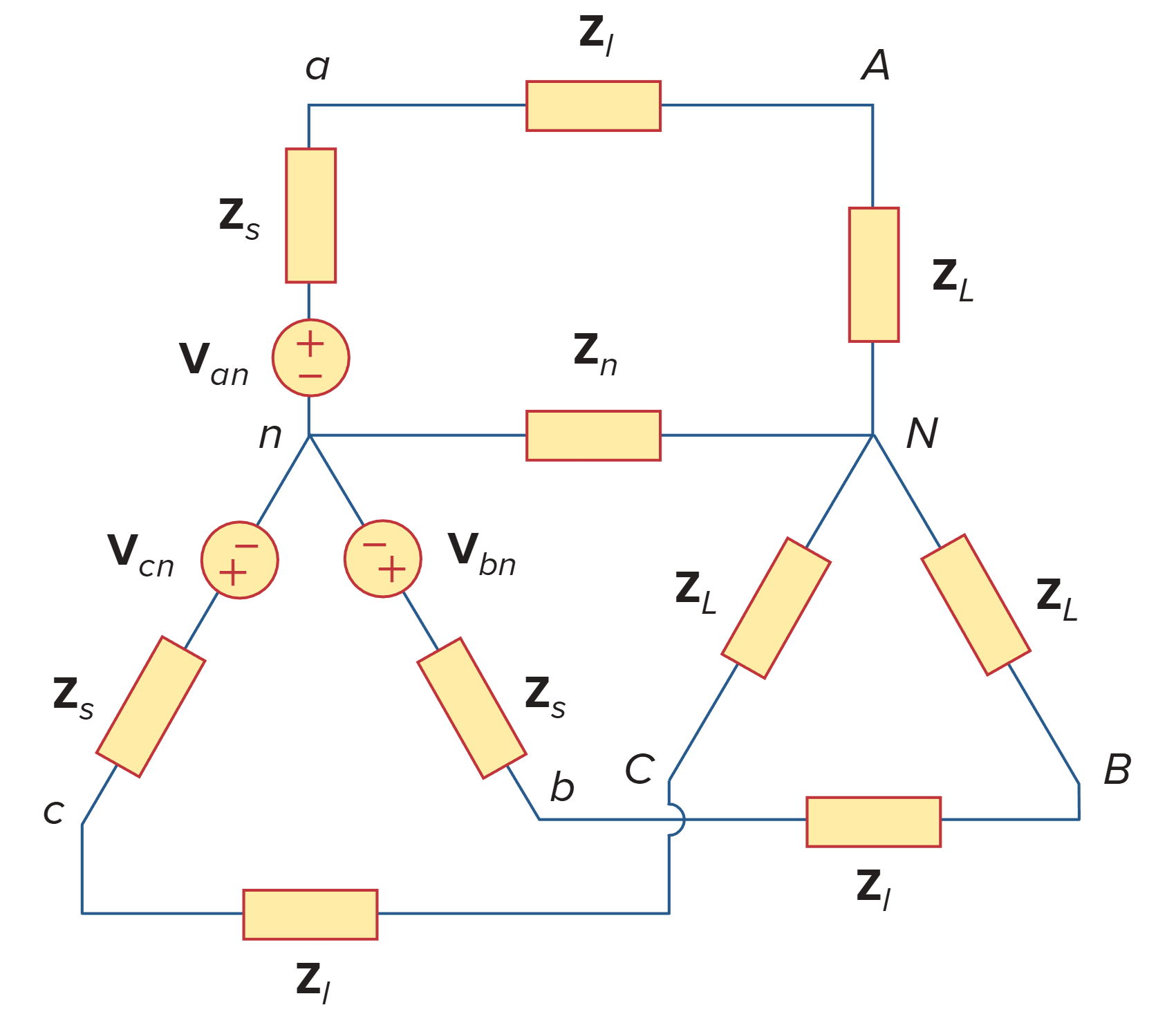
通常，Z_s 和 Z_ℓ 相比 Z_L 非常小，因此可以假设 Z_Y = Z_L（如果Z_s 和 Z_ℓ没有给定，则默认它们为零）。

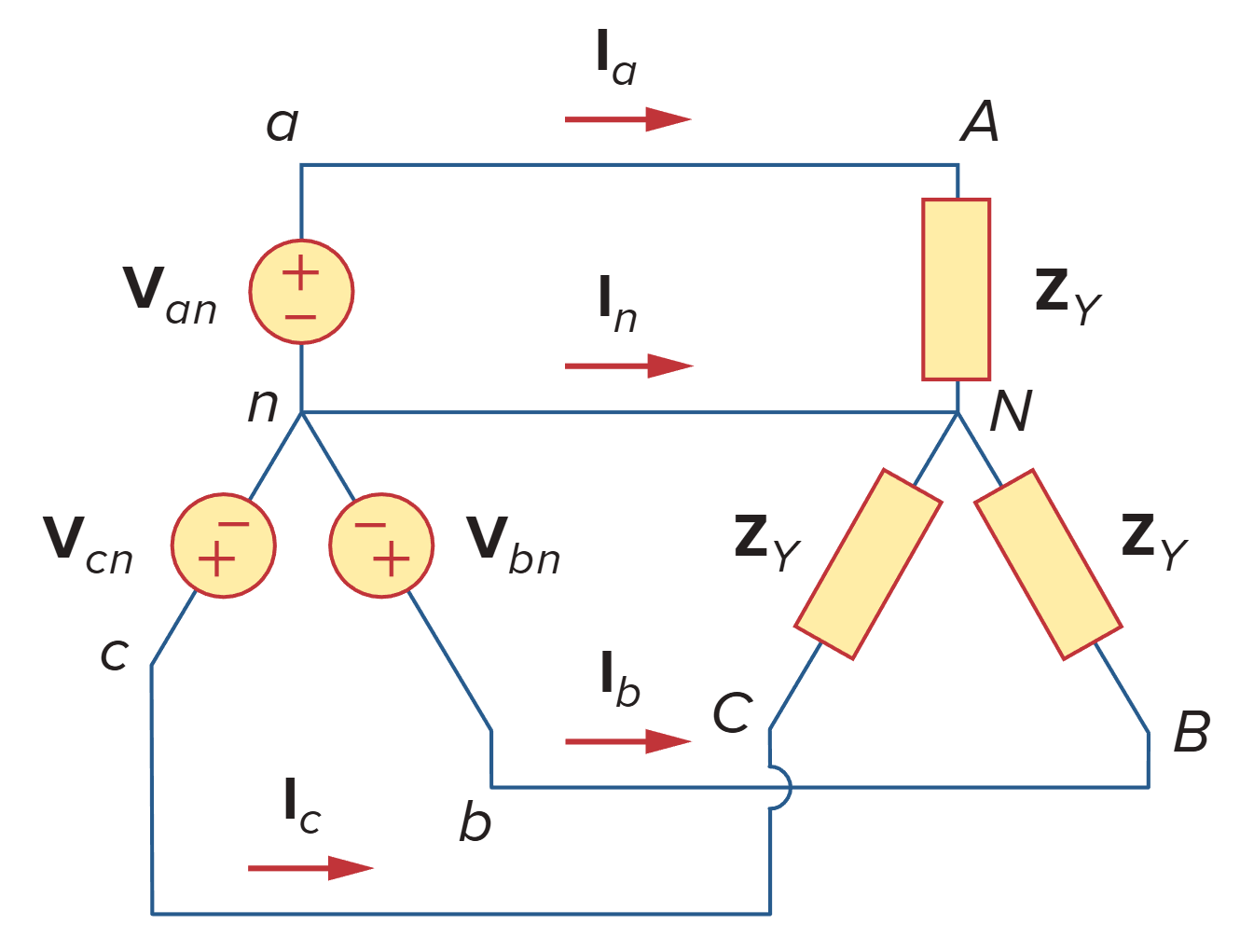
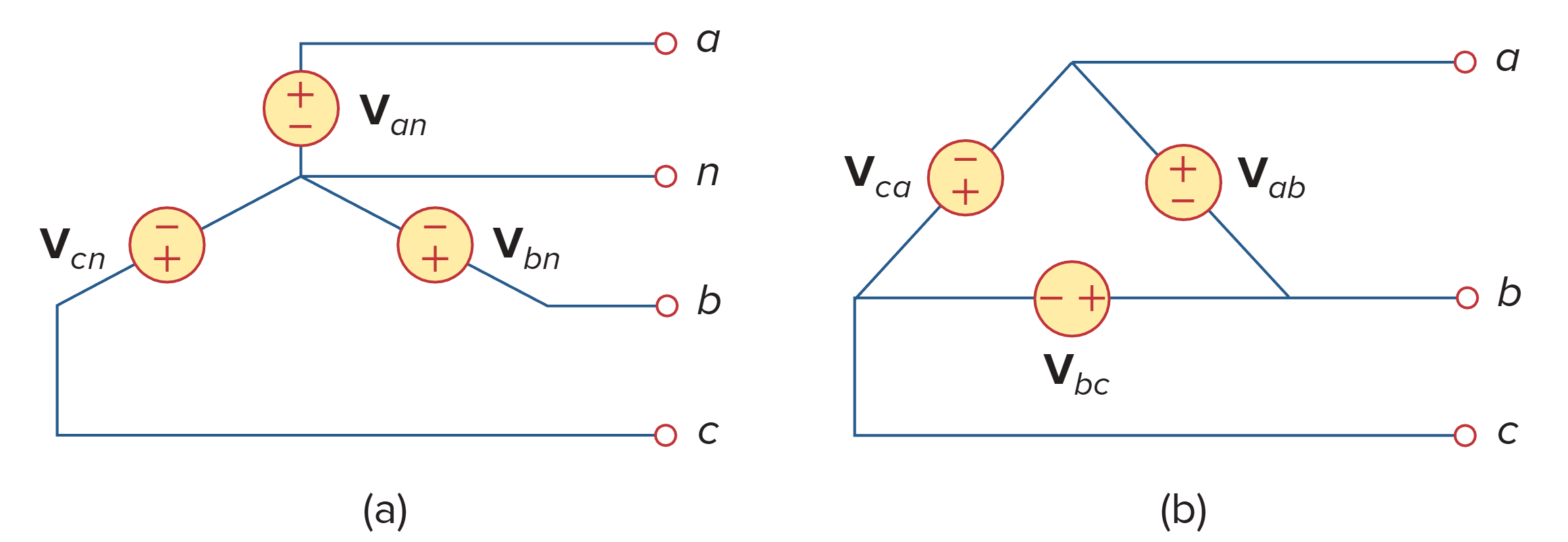
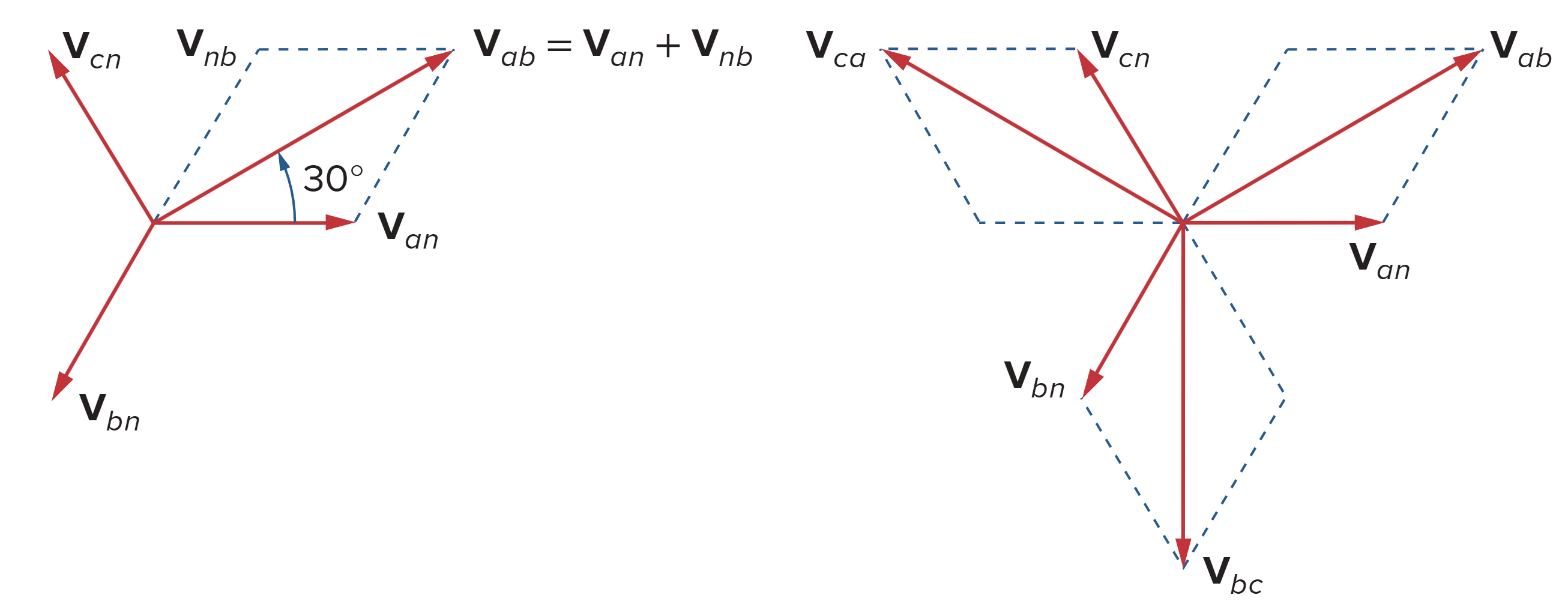
The line-to-line voltages or simply line voltages are related to the phase voltages.

线电压的计算：

$$\begin{array}{rl}{\mathbf{V}}_{ab}& ={\mathbf{V}}_{an}+{\mathbf{V}}_{nb}={\mathbf{V}}_{an}-{\mathbf{V}}_{bn}\\ & =V_p\mathrm{\angle }0\mathrm{°}-V_p\mathrm{\angle }-120\mathrm{°}\\ & =V_p(\cos 0\mathrm{°}+j\sin 0\mathrm{°}-\cos (-120\mathrm{°})-j\sin (-120\mathrm{°}))\\ & =V_p(1+0+\frac{1}{2}+j\frac{\sqrt{3}}{2})\\ & =\sqrt{3}{V}_p\mathrm{\angle }30\mathrm{°}\\ \text{Similarly,}{\mathbf{V}}_{bc}& =\sqrt{3}{V}_p\mathrm{\angle }-90\mathrm{°}\\ {\mathbf{V}}_{ca}& =\sqrt{3}{V}_p\mathrm{\angle }-210\mathrm{°}\end{array}$$

因此，线电压（火线与火线之间的电压） V_L 的大小为 $\sqrt{3}$ 倍的相电压（火线与零线之间的电压） V_p，并且线电压的相位比相电压的相位超前 30°。

The line voltages lead their corresponding phase voltages by 30°.

$$\begin{array}{rl}& V_L=\sqrt{3}{V}_p\\ & V_p=|{\mathbf{V}}_{an}|=|{\mathbf{V}}_{bn}|=|{\mathbf{V}}_{cn}|\\ & V_L=|{\mathbf{V}}_{ab}|=|{\mathbf{V}}_{bc}|=|{\mathbf{V}}_{ca}|\end{array}$$

线电流的计算：

$$\begin{array}{rl}& {\mathbf{I}}_a=\frac{{\mathbf{V}}_{an}}{{\mathbf{Z}}_Y}\\ & {\mathbf{I}}_b=\frac{{\mathbf{V}}_{bn}}{{\mathbf{Z}}_Y}=\frac{{\mathbf{V}}_{an}\mathrm{\angle }-120\mathrm{°}}{{\mathbf{Z}}_Y}={\mathbf{I}}_a\mathrm{\angle }-120\mathrm{°}\\ & {\mathbf{I}}_c=\frac{{\mathbf{V}}_{cn}}{{\mathbf{Z}}_Y}=\frac{{\mathbf{V}}_{an}\mathrm{\angle }-240\mathrm{°}}{{\mathbf{Z}}_Y}={\mathbf{I}}_a\mathrm{\angle }-240\mathrm{°}\\ & {\mathbf{I}}_a+{\mathbf{I}}_b+{\mathbf{I}}_c=0\\ & {\mathbf{I}}_n=-({\mathbf{I}}_a+{\mathbf{I}}_b+{\mathbf{I}}_c)=0\\ & {\mathbf{V}}_{nN}={\mathbf{Z}}_n{\mathbf{I}}_n=0\end{array}$$

即中性线（零线）上的电压为零。因此，可以去掉中性线而不影响系统。实际上，在长距离电力传输中，使用的是三根或其倍数的导线，而以大地本身作为中性导体。如此设计的电力系统在所有关键点都进行了良好的接地，以确保安全。

Y-∆

Balanced Y-∆ Connection

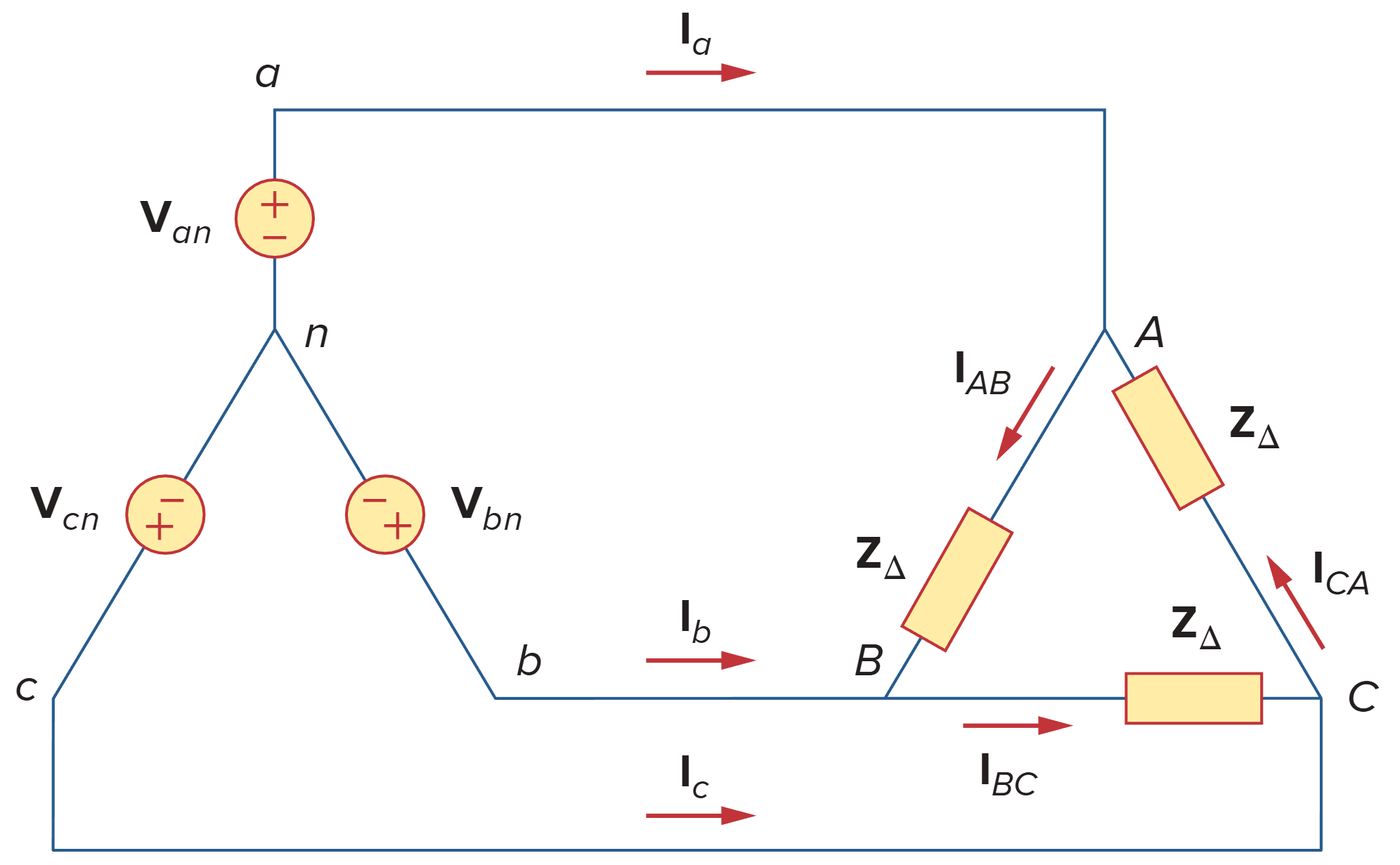
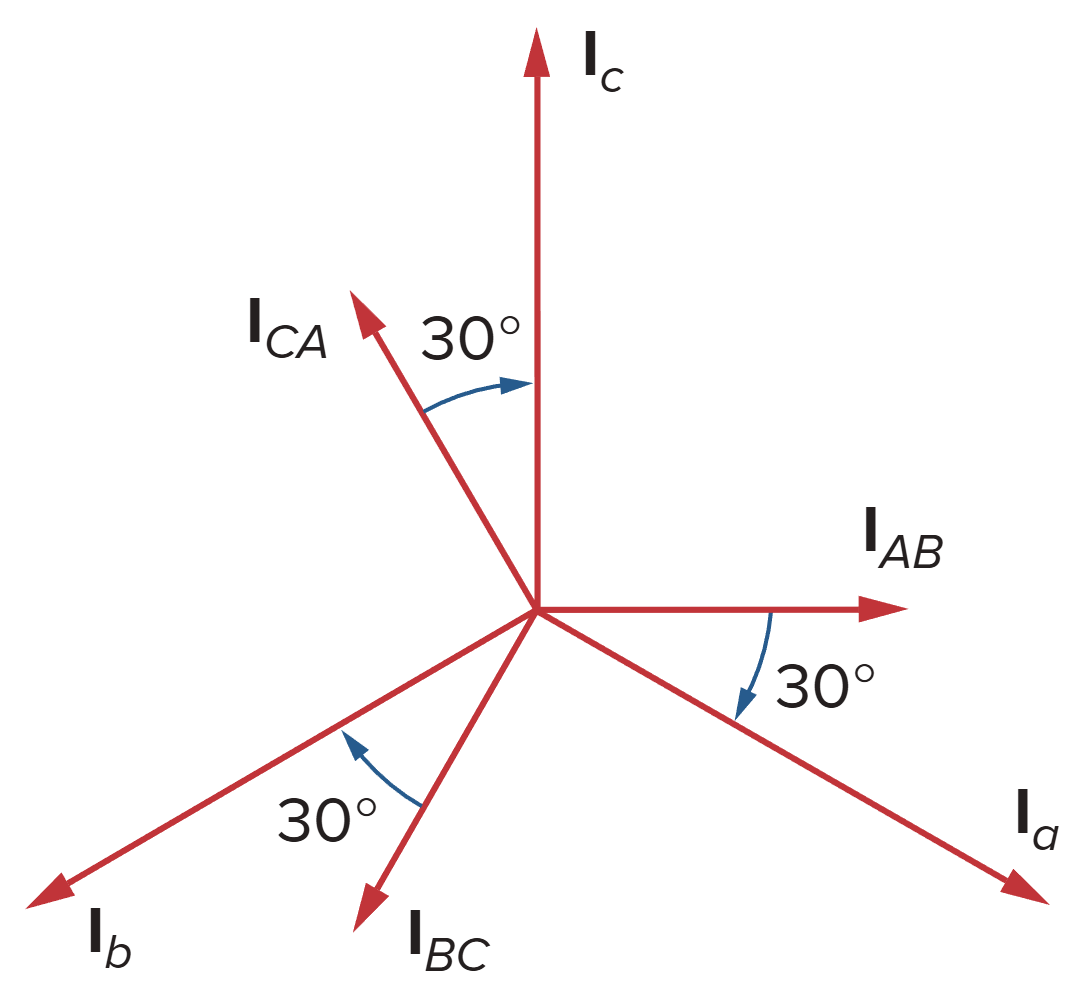
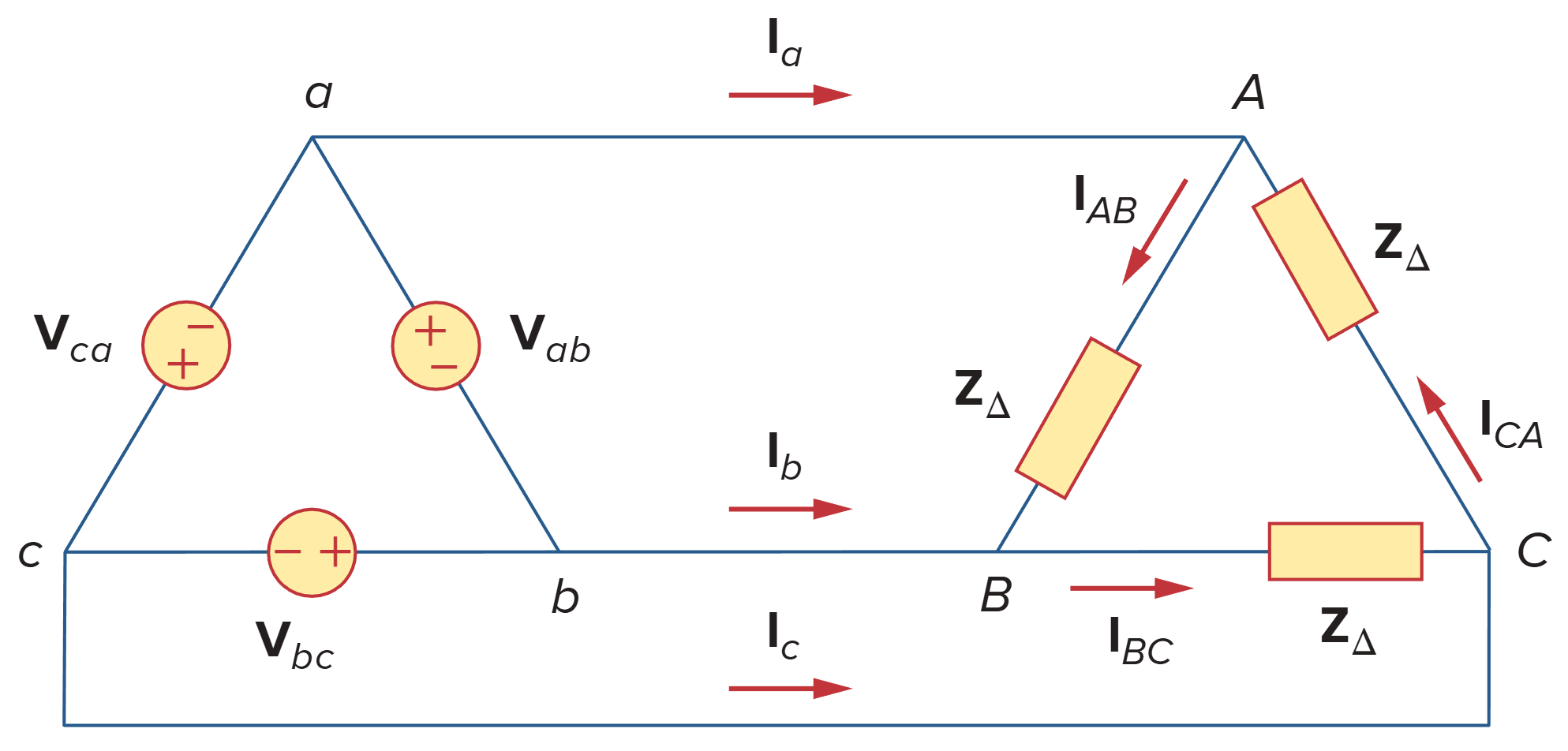
如图所示，其中

• ${\mathbf{V}}_{an},{\mathbf{V}}_{bn},{\mathbf{V}}_{cn}$ 为相电压
• ${\mathbf{Z}}_{\mathrm{\Delta }}$ 为三角形负载阻抗
• ${\mathbf{V}}_{AB},{\mathbf{V}}_{BC},{\mathbf{V}}_{CA}$ 为线电压（负载电压）
• ${\mathbf{I}}_{AB},{\mathbf{I}}_{BC},{\mathbf{I}}_{CA}$ 为相电流（负载电流）
• ${\mathbf{I}}_a,{\mathbf{I}}_b,{\mathbf{I}}_c$ 为线电流

另外，规定

• 相电压的幅值为 $V_p$
• 负载阻抗两端电压的幅值为 $V_Z$
• 相电流的幅值为 $I_p$
• 线电流的幅值为 $I_L$

import sympy as sp # 导入 sympy 库并简写为 sp
from IPython.display import display, Math, HTML

j = sp.I  # 定义虚数单位 j

# 列出已知量
V_p = sp.symbols('V_p', real=True, positive=True) # 正实数
V_an = V_p * sp.exp(j * 0) # 复数
V_bn = V_p * sp.exp(j * sp.rad(-120)) # 复数
V_cn = V_p * sp.exp(j * sp.rad(120)) # 复数
Z_Delta = sp.symbols(r'\mathbf{Z}_{\Delta}', complex=True) # 复数
# 打印已知量
display(Math(sp.latex(sp.Eq(sp.Symbol('V_p'), V_p)))), 
display(Math(sp.latex(sp.Eq(sp.Symbol(r'\mathbf{V}_{an}'), V_an)))), 
display(Math(sp.latex(sp.Eq(sp.Symbol(r'\mathbf{V}_{bn}'), V_bn)))), 
display(Math(sp.latex(sp.Eq(sp.Symbol(r'\mathbf{V}_{cn}'), V_cn)))), 
display(Math(sp.latex(sp.Eq(sp.Symbol(r'\mathbf{Z}_{\Delta}'), Z_Delta))))

# 优化打印（极坐标形式）
display(HTML('<p><b>优化打印（极坐标形式）：</b></p>'))
def display_polar(name, expr):
    r = sp.nsimplify(sp.sqrt(sp.re(expr)**2 + sp.im(expr)**2))
    theta = sp.deg(sp.atan2(sp.im(expr), sp.re(expr)))
    display(Math(rf"{name} = {sp.latex(r)}\,\angle\,{sp.latex(theta)}^\circ"))
    
display_polar(r'\mathbf{V}_{an}', V_an)
display_polar(r'\mathbf{V}_{bn}', V_bn)
display_polar(r'\mathbf{V}_{cn}', V_cn)

${\displaystyle V_p=V_p}$

${\displaystyle {\mathbf{V}}_{an}=V_p}$

${\displaystyle {\mathbf{V}}_{bn}=V_p{e}^{-\frac{2i\pi }{3}}}$

${\displaystyle {\mathbf{V}}_{cn}=V_p{e}^{\frac{2i\pi }{3}}}$

${\displaystyle {\mathbf{Z}}_{\mathrm{\Delta }}={\mathbf{Z}}_{\mathrm{\Delta }}}$

优化打印（极坐标形式）：

${\displaystyle {\mathbf{V}}_{an}=V_p\mathrm{\angle }{0}^{\circ }}$

${\displaystyle {\mathbf{V}}_{bn}=V_p\mathrm{\angle }-{120}^{\circ }}$

${\displaystyle {\mathbf{V}}_{cn}=V_p\mathrm{\angle }{120}^{\circ }}$

# 求解线电压
display(HTML('<p><b>线电压（负载电压）：</b></p>'))
# 如图，显然 
# V_AB = V_an + V_nb = V_an - V_bn, 
# V_BC = V_bn + V_nc = V_bn - V_cn, 
# V_CA = V_cn + V_na = V_cn - V_an
# 因此
V_AB = V_an - V_bn
V_BC = V_bn - V_cn
V_CA = V_cn - V_an
# 打印线电压
display(Math(sp.latex(sp.Eq(sp.Symbol(r'\mathbf{V}_{AB}'), V_AB))))
display(Math(sp.latex(sp.Eq(sp.Symbol(r'\mathbf{V}_{BC}'), V_BC))))
display(Math(sp.latex(sp.Eq(sp.Symbol(r'\mathbf{V}_{CA}'), V_CA))))

# 优化打印（极坐标形式）
display(HTML('<p><b>优化打印（极坐标形式）：</b></p>'))
def display_polar(name, expr):
    r = sp.nsimplify(sp.sqrt(sp.re(expr)**2 + sp.im(expr)**2))
    theta = sp.nsimplify(sp.deg(sp.atan2(sp.im(expr), sp.re(expr))))
    display(Math(sp.latex(sp.Symbol(name)) + '=' + sp.latex(r) + r'\angle' + sp.latex(theta) + r'\degree'))

display_polar(r'\mathbf{V}_{AB}', V_AB)
display_polar(r'\mathbf{V}_{BC}', V_BC)
display_polar(r'\mathbf{V}_{CA}', V_CA)

# 因此，$V_Z = \sqrt{3}V_p$
display(HTML('<p><b>因此，负载的端电压的幅值是相电压的根号3倍。</b></p>'))
display(Math(fr'$V_Z = \sqrt{3} V_p$'))

线电压（负载电压）：

${\displaystyle {\mathbf{V}}_{AB}=V_p-V_p{e}^{-\frac{2i\pi }{3}}}$

${\displaystyle {\mathbf{V}}_{BC}=V_p{e}^{-\frac{2i\pi }{3}}-V_p{e}^{\frac{2i\pi }{3}}}$

${\displaystyle {\mathbf{V}}_{CA}=-V_p+V_p{e}^{\frac{2i\pi }{3}}}$

优化打印（极坐标形式）：

${\displaystyle {\mathbf{V}}_{AB}=\sqrt{3}{V}_p\mathrm{\angle }30\mathrm{°}}$

${\displaystyle {\mathbf{V}}_{BC}=\sqrt{3}{V}_p\mathrm{\angle }-90\mathrm{°}}$

${\displaystyle {\mathbf{V}}_{CA}=\sqrt{3}{V}_p\mathrm{\angle }150\mathrm{°}}$

因此，负载的端电压的幅值是相电压的根号3倍。

${\displaystyle V_Z=\sqrt{3}{V}_p}$

# 相电流 I_AB, I_BC, I_CA 的幅值为 I_p
# 线电流 I_a, I_b, I_c 的幅值为 I_L
# 在节点 A, B, C 处，应用 KCL
# I_a = I_AB - I_CA,
# I_b = I_BC - I_AB,
# I_c = I_CA - I_BC

# 相电流（复数） I_p: I_AB, I_BC, I_CA
I_AB = V_AB / Z_Delta
I_BC = V_BC / Z_Delta
I_CA = V_CA / Z_Delta
# 打印相电流
display(HTML('<p><b>相电流：</b></p>'))
display(Math(sp.latex(sp.Eq(sp.Symbol(r'\mathbf{I}_{AB}'), I_AB))))
display(Math(sp.latex(sp.Eq(sp.Symbol(r'\mathbf{I}_{BC}'), I_BC))))
display(Math(sp.latex(sp.Eq(sp.Symbol(r'\mathbf{I}_{CA}'), I_CA))))

相电流：

${\displaystyle {\mathbf{I}}_{AB}=\frac{V_p-V_p{e}^{-\frac{2i\pi }{3}}}{{\mathbf{Z}}_{\mathrm{\Delta }}}}$

${\displaystyle {\mathbf{I}}_{BC}=\frac{V_p{e}^{-\frac{2i\pi }{3}}-V_p{e}^{\frac{2i\pi }{3}}}{{\mathbf{Z}}_{\mathrm{\Delta }}}}$

${\displaystyle {\mathbf{I}}_{CA}=\frac{-V_p+V_p{e}^{\frac{2i\pi }{3}}}{{\mathbf{Z}}_{\mathrm{\Delta }}}}$

# 线电流（复数） I_L: I_a, I_b, I_c
I_a = I_AB - I_CA
I_b = I_BC - I_AB
I_c = I_CA - I_BC
# 打印线电流
display(HTML('<p><b>线电流：</b></p>'))
display(Math(sp.latex(sp.Eq(sp.Symbol(r'\mathbf{I}_a'), I_a))))
display(Math(sp.latex(sp.Eq(sp.Symbol(r'\mathbf{I}_b'), I_b))))
display(Math(sp.latex(sp.Eq(sp.Symbol(r'\mathbf{I}_c'), I_c))))

线电流：

${\displaystyle {\mathbf{I}}_a=-\frac{-V_p+V_p{e}^{\frac{2i\pi }{3}}}{{\mathbf{Z}}_{\mathrm{\Delta }}}+\frac{V_p-V_p{e}^{-\frac{2i\pi }{3}}}{{\mathbf{Z}}_{\mathrm{\Delta }}}}$

${\displaystyle {\mathbf{I}}_b=-\frac{V_p-V_p{e}^{-\frac{2i\pi }{3}}}{{\mathbf{Z}}_{\mathrm{\Delta }}}+\frac{V_p{e}^{-\frac{2i\pi }{3}}-V_p{e}^{\frac{2i\pi }{3}}}{{\mathbf{Z}}_{\mathrm{\Delta }}}}$

${\displaystyle {\mathbf{I}}_c=\frac{-V_p+V_p{e}^{\frac{2i\pi }{3}}}{{\mathbf{Z}}_{\mathrm{\Delta }}}-\frac{V_p{e}^{-\frac{2i\pi }{3}}-V_p{e}^{\frac{2i\pi }{3}}}{{\mathbf{Z}}_{\mathrm{\Delta }}}}$

# 线电流的幅值和相电流的幅值的比值关系
ratio = sp.Abs(I_a) / sp.Abs(I_AB) # 通过 sympy 计算比值
display(Math(r'\frac{I_L}{I_p} = ' + sp.latex(ratio.simplify())))
display(HTML('<p><b>因此，线电流的幅值是相电流幅值的根号3倍。</b></p>'))
display(Math(r'I_L = ' + sp.latex(ratio.simplify()) + r' I_p'))

${\displaystyle \frac{I_L}{I_p}=\sqrt{3}}$

因此，线电流的幅值是相电流幅值的根号3倍。

${\displaystyle I_L=\sqrt{3}{I}_p}$

补充

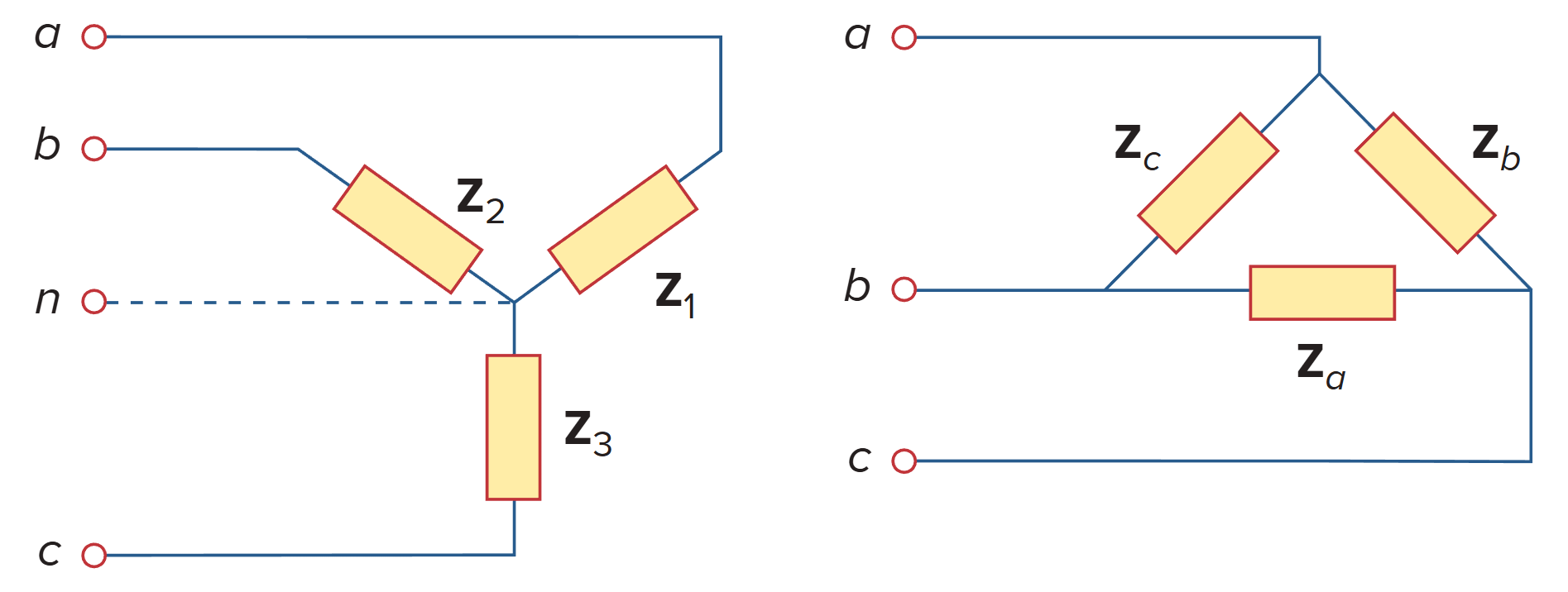
对于 ∆ 形负载，可以将其转换为 Y 形负载，然后进行分析

$${\mathbf{Z}}_Y=\frac{{\mathbf{Z}}_{\mathrm{\Delta }}}{3}$$

根据欧姆定律，线电流的幅值可以表示为相电压与负载阻抗的模的比值。

$$I_L=\left|\frac{{\mathbf{V}}_p}{{\mathbf{Z}}_Y}\right|=3\left|\frac{{\mathbf{V}}_p}{{\mathbf{Z}}_{\mathrm{\Delta }}}\right|$$

其中 $|{\mathbf{V}}_p|=|{\mathbf{V}}_{an}|=|{\mathbf{V}}_{bn}|=|{\mathbf{V}}_{cn}|$。

∆-∆

如图所示。

相电压等于线电压

$${\mathbf{V}}_{ab}={\mathbf{V}}_{AB},{\mathbf{V}}_{bc}={\mathbf{V}}_{BC},{\mathbf{V}}_{ca}={\mathbf{V}}_{CA}$$

于是相电流（负载电流）为

$${\mathbf{I}}_{AB}=\frac{{\mathbf{V}}_{AB}}{{\mathbf{Z}}_{\mathrm{\Delta }}}=\frac{{\mathbf{V}}_{ab}}{{\mathbf{Z}}_{\mathrm{\Delta }}},{\mathbf{I}}_{BC}=\frac{{\mathbf{V}}_{BC}}{{\mathbf{Z}}_{\mathrm{\Delta }}}=\frac{{\mathbf{V}}_{bc}}{{\mathbf{Z}}_{\mathrm{\Delta }}},{\mathbf{I}}_{CA}=\frac{{\mathbf{V}}_{CA}}{{\mathbf{Z}}_{\mathrm{\Delta }}}=\frac{{\mathbf{V}}_{ca}}{{\mathbf{Z}}_{\mathrm{\Delta }}}$$

由于负载呈 ∆ 形，所以线电流为

$$I_L=\sqrt{3}{I}_p$$

∆-Y

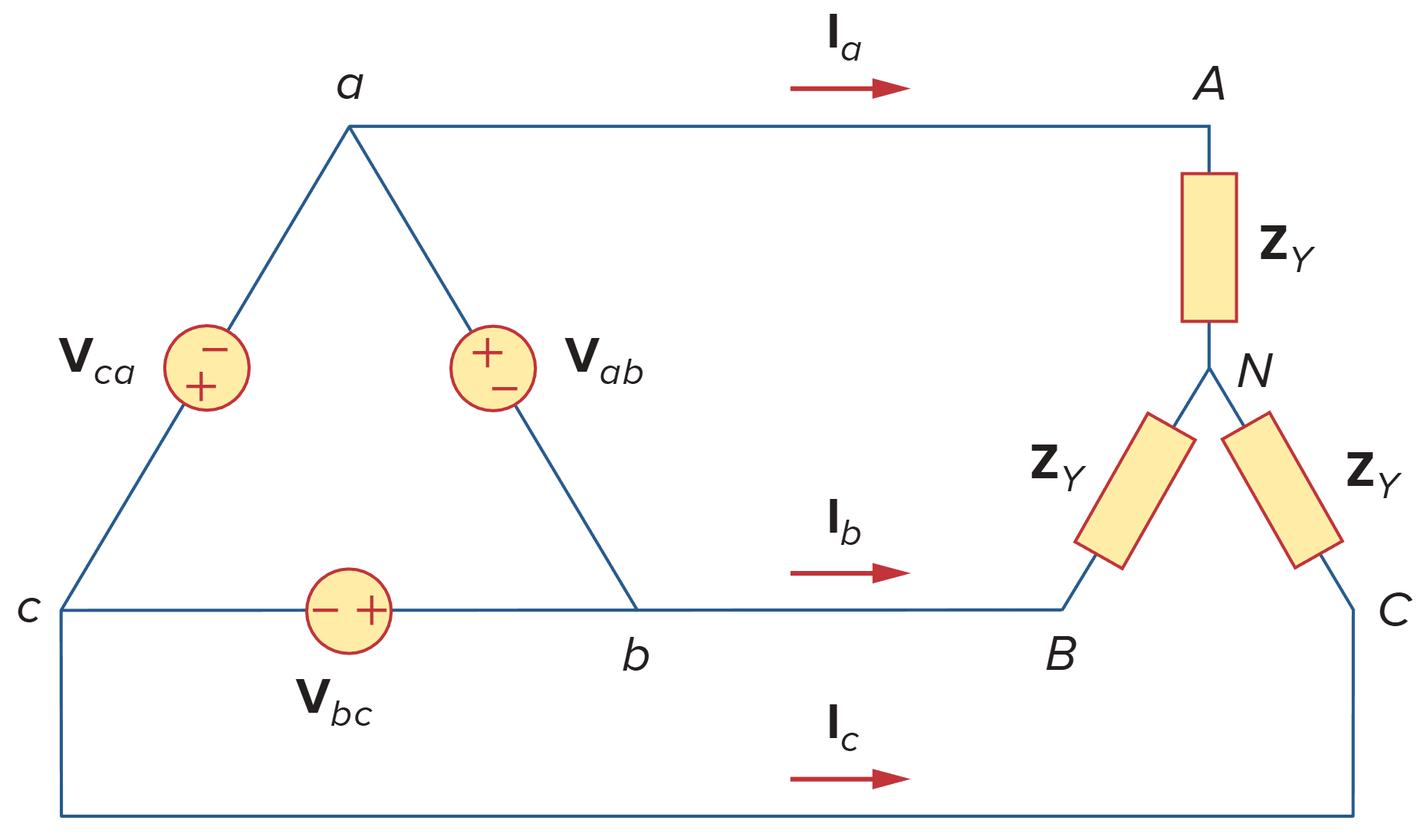
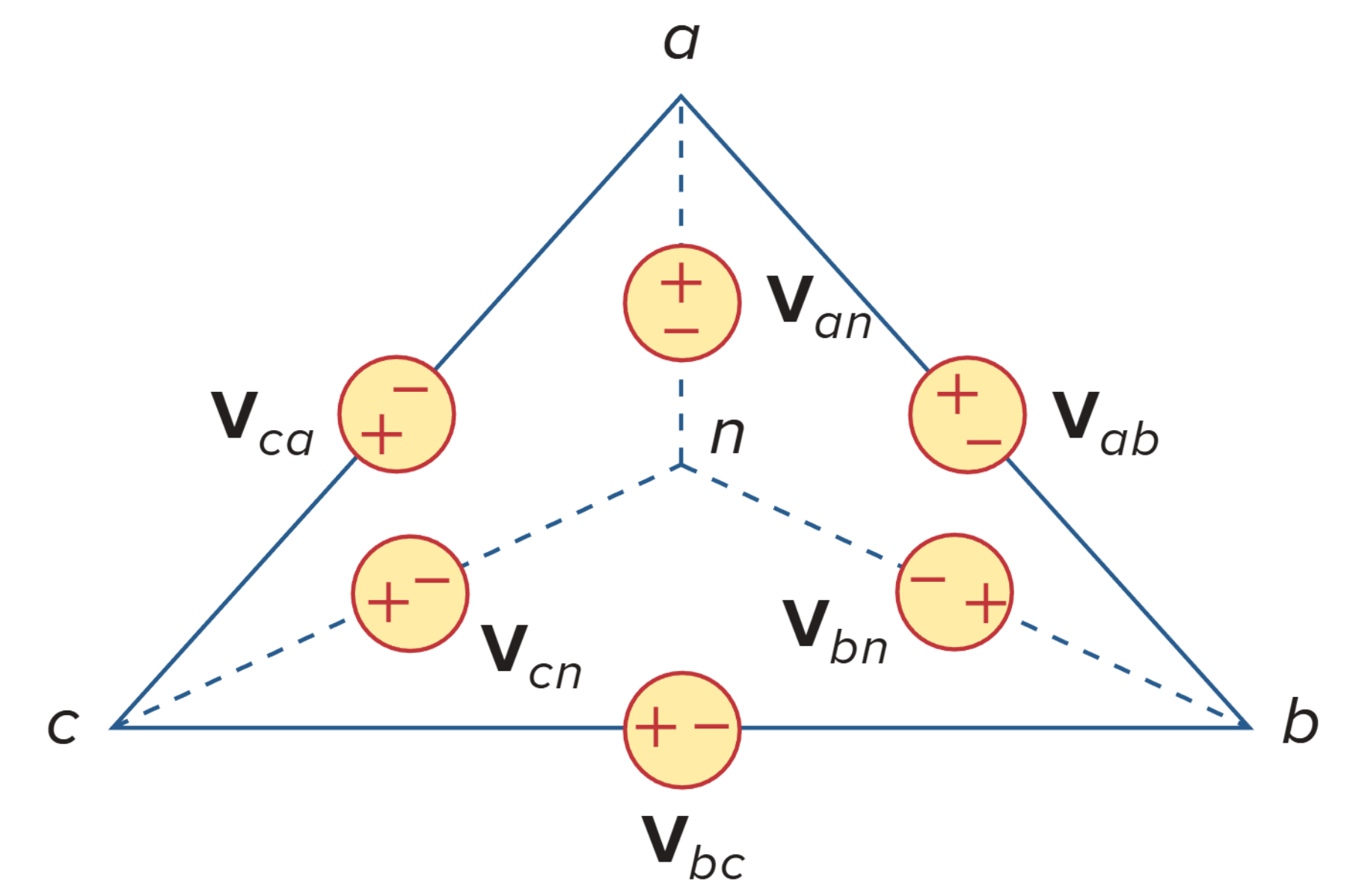
将 ∆ 形电源转换为 Y 形电源，得到

$${\mathbf{V}}_{an}=\frac{V_p}{\sqrt{3}}\mathrm{\angle }-30\mathrm{°},{\mathbf{V}}_{bn}=\frac{V_p}{\sqrt{3}}\mathrm{\angle }-150\mathrm{°},{\mathbf{V}}_{cn}=\frac{V_p}{\sqrt{3}}\mathrm{\angle }+90\mathrm{°}$$

线电流为

$${\mathbf{I}}_a=\frac{V_p/\sqrt{3}\mathrm{\angle }-30\mathrm{°}}{Z_Y},{\mathbf{I}}_b=\frac{V_p/\sqrt{3}\mathrm{\angle }-150\mathrm{°}}{Z_Y},{\mathbf{I}}_c=\frac{V_p/\sqrt{3}\mathrm{\angle }+90\mathrm{°}}{Z_Y}$$

相电压（负载电压）为

$${\mathbf{V}}_{AN}={\mathbf{I}}_a{\mathbf{Z}}_Y=\frac{V_p}{\sqrt{3}}\mathrm{\angle }-30\mathrm{°},{\mathbf{V}}_{BN}={\mathbf{V}}_{AN}\mathrm{\angle }-120\mathrm{°},{\mathbf{V}}_{CN}={\mathbf{V}}_{AN}\mathrm{\angle }+120\mathrm{°}$$

平衡系统中的功率

Power in Balanced Systems

恒定总瞬时功率

考虑 Y-Y 连接的平衡三相系统

对于 Y 形负载

$$\begin{array}{rl}& v_{AN}=\sqrt{2}{V}_p\cos \omega t\\ & v_{BN}=\sqrt{2}{V}_p\cos (\omega t-120\mathrm{°})\\ & v_{CN}=\sqrt{2}{V}_p\cos (\omega t+120\mathrm{°})\end{array}$$

其中，V_p 是 rms 值，所以要乘以 √2 得到峰值。

如果负载阻抗为 Z_Y = Z ∠θ，则对应的相电流相对于相电压滞后 θ 角。因此

$$\begin{array}{rl}& i_a=\sqrt{2}{I}_p\cos (\omega t-\theta )\\ & i_b=\sqrt{2}{I}_p\cos (\omega t-\theta -120\mathrm{°})\\ & i_c=\sqrt{2}{I}_p\cos (\omega t-\theta +120\mathrm{°})\end{array}$$

其中，I_p 是 rms 值，所以要乘以 √2 得到峰值。

Y 型负载的总瞬时功率

$$\begin{array}{rl}p& =p_a+p_b+p_c\\ & =v_{AN}{i}_a+v_{BN}{i}_b+v_{CN}{i}_c\\ & =2V_p{I}_p[\cos \omega t\cos (\omega t-\theta )\\ & \phantom{=2V_p{I}_p}+\cos (\omega t-120\mathrm{°})\cos (\omega t-\theta -120\mathrm{°})\\ & \phantom{=2V_p{I}_p}+\cos (\omega t+120\mathrm{°})\cos (\omega t-\theta +120\mathrm{°})]\end{array}$$

应用三角函数积化和差公式 $\cos A\cos B=\frac{1}{2}[\cos (A+B)+\cos (A-B)]$ ，得到

$$\begin{array}{rl}p& =V_p{I}_p[\cos (2\omega t-\theta )+\cos (\theta )\\ & \phantom{=V_p{I}_p}+\cos (2\omega t-\theta -240\mathrm{°})+\cos (\theta )\\ & \phantom{=V_p{I}_p}+\cos (2\omega t-\theta +240\mathrm{°})+\cos (\theta )]\\ & =V_p{I}_p[3\cos \theta +\cos \alpha +\cos (\alpha -240\mathrm{°})+\cos (\alpha +240\mathrm{°})]\\ & \phantom{=}\text{ where }\alpha =2\omega t-\theta \\ & =V_p{I}_p[3\cos \theta +\cos \alpha \\ & \phantom{=V_p{I}_p}+\cos \alpha \cos 240\mathrm{°}+\sin \alpha \sin 240\mathrm{°}\\ & \phantom{=V_p{I}_p}+\cos \alpha \cos 240\mathrm{°}-\sin \alpha \sin 240\mathrm{°}]\\ & =V_p{I}_p[3\cos \theta +\cos \alpha -1/2\cos \alpha -1/2\cos \alpha ]\\ & =3V_p{I}_p\cos \theta \end{array}$$

因此，平衡三相系统中的总瞬时功率是恒定的。这个结果对于 Y 型和 ∆ 型负载（回想一下，∆ 型可以转换为 Y 型，反之亦然）都成立。这是使用三相系统进行发电和配电的重要原因之一。

由于总瞬时功率与时间无关，因此对于 Y 型或 ∆ 型负载，每相的平均功率均为 p/3

$$\begin{array}{rl}& P_p=V_p{I}_p\cos \theta \\ & Q_p=V_p{I}_p\sin \theta \\ & S_p=V_p{I}_p\\ & {\mathbf{S}}_p=P_p+j{Q}_p={\mathbf{V}}_p{\mathbf{I}}_p^{\ast }\end{array}$$

总的平均功率为

$$\begin{array}{rl}& P=3P_p=3V_p{I}_p\cos \theta =\sqrt{3}{V}_L{I}_L\cos \theta \\ & Q=3Q_p=3V_p{I}_p\sin \theta =\sqrt{3}{V}_L{I}_L\sin \theta \end{array}$$

总的复功率为

$$\begin{array}{rl}& \mathbf{S}=3{\mathbf{S}}_p=3{\mathbf{V}}_p{\mathbf{I}}_p^{\ast }=3I_p^2{\mathbf{Z}}_p=\frac{3V_p^2}{{\mathbf{Z}}_p^{\ast }}\\ & \mathbf{S}=P+jQ=\sqrt{3}{V}_L{I}_L(\cos \theta +j\sin \theta )=\sqrt{3}{V}_L{I}_L\mathrm{\angle }\theta \end{array}$$

以上功率分析只考虑了 Y-Y 连接的平衡三相系统。对于其它连接系统，可以考虑转换为 Y-Y 连接的平衡三相系统，然后进行分析。

导线材料消耗

对于相同的负载电压 V_L 和相同的传输损耗功率 P_L，三相系统所需的导线材料消耗少于单相系统。

这里的 L 指 Load 而不是 Line 。

PS: 教材在分析 Y-Y 连接时，使用 V_L 表示线电压，在这里却又用 V_L 表示负载电压。搞得我开始时没有看明白 P^'_loss 。实际上其分母整体代表的是线电压的平方。而在 Y-Y 连接中，线电压是相电压（负载电压）的 √3 倍。

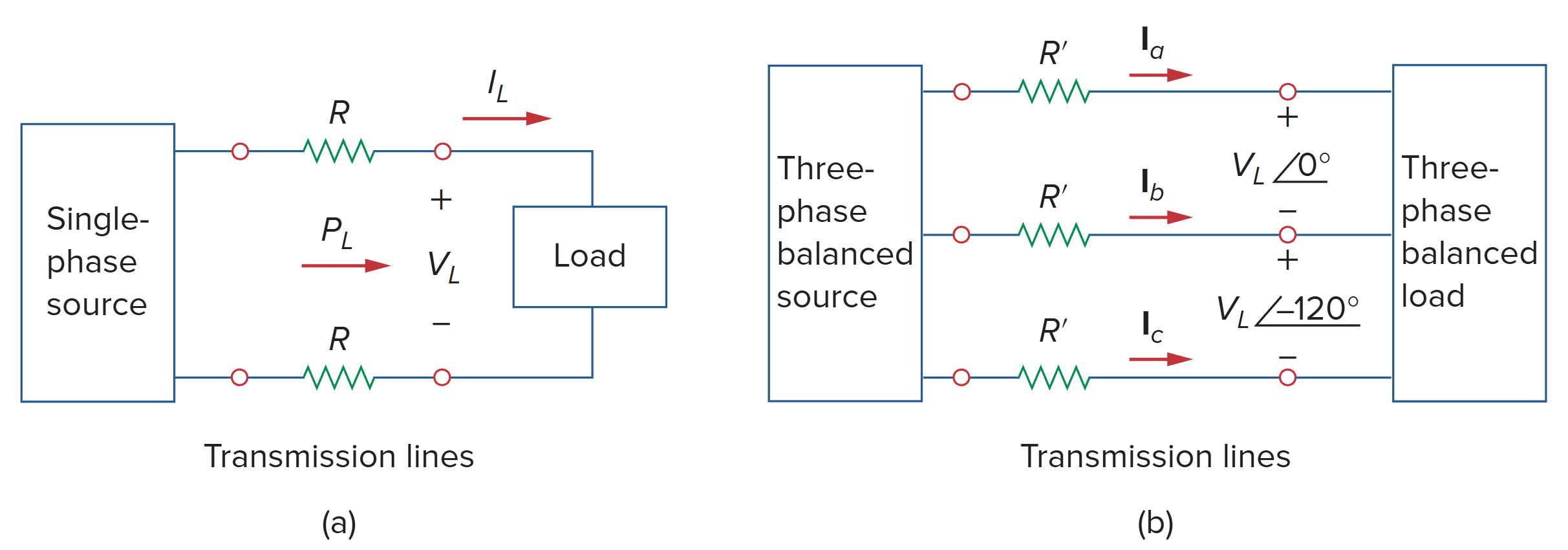
单相系统功率消耗为

$$P_{\text{loss}}=2I_L^{2}R=2R\frac{P_L^2}{V_L^2}$$

三相系统功率消耗为

$$P_{\text{loss}}^{\prime }=3(I_L^{\prime }{)}^2{R}^{\prime }=3R^{\prime }\frac{P_L^2}{3V_L^2}=R^{\prime }\frac{P_L^2}{V_L^2}$$

功率消耗比值为

$$\frac{P_{\text{loss}}}{P_{\text{loss}}^{\prime }}=\frac{2R}{R^{\prime }}d$$

其中，根据大学物理知识，导线的电阻 $R$ 与其长度 $l$ 和材料的电阻率 $\rho$ 成正比，与横截面积 $A$ 成反比，即 $R={\displaystyle \frac{\rho l}{\pi r^2}}$。因此

$$\frac{P_{\text{loss}}}{P_{\text{loss}}^{\prime }}=\frac{2R}{R^{\prime }}=\frac{2{\displaystyle \frac{\rho l}{\pi r^2}}}{{\displaystyle \frac{\rho l}{\pi r^{\prime 2}}}}=\frac{2r^{\prime 2}}{r^2}$$

因为 $P_{\text{loss}}=P_{\text{loss}}^{\prime }$，所以 ${\displaystyle \frac{2r^{\prime 2}}{r^2}=1}$，即 ${\displaystyle \frac{r^2}{r^{\prime 2}}=2}$。

计算导线材料消耗的比值

$$\begin{array}{rl}\frac{\text{Material for single-phase}}{\text{Material for three-phase}}& =\frac{2}{3}\frac{\pi r^{2}l}{\pi {r^{\prime }}^{2}l}\\ & =\frac{2}{3}\cdot 2=1.333\end{array}$$

由上述计算可知，单相系统在同样条件下所需的导线材料比三相系统多出约 33%，也就是说，三相系统所消耗的导线材料仅为等效单相系统的 75%。