质点的平衡

在静力学中，当多个共点力（concurrent force system）作用在一个质点上，若其合力为零，则该质点处于平衡状态。此类问题通常通过向量分解、合成和平衡条件来求解未知力的大小和方向。

质点的平衡公式

F_{R} = Σ F = 0

二维空间

\begin{aligned} Σ F_{x} & = 0 \\ Σ F_{y} & = 0 \end{aligned}

三维空间

\begin{aligned} Σ F_{x} & = 0 \\ Σ F_{y} & = 0 \\ Σ F_{z} & = 0 \end{aligned}

示例

平面受力分析 1

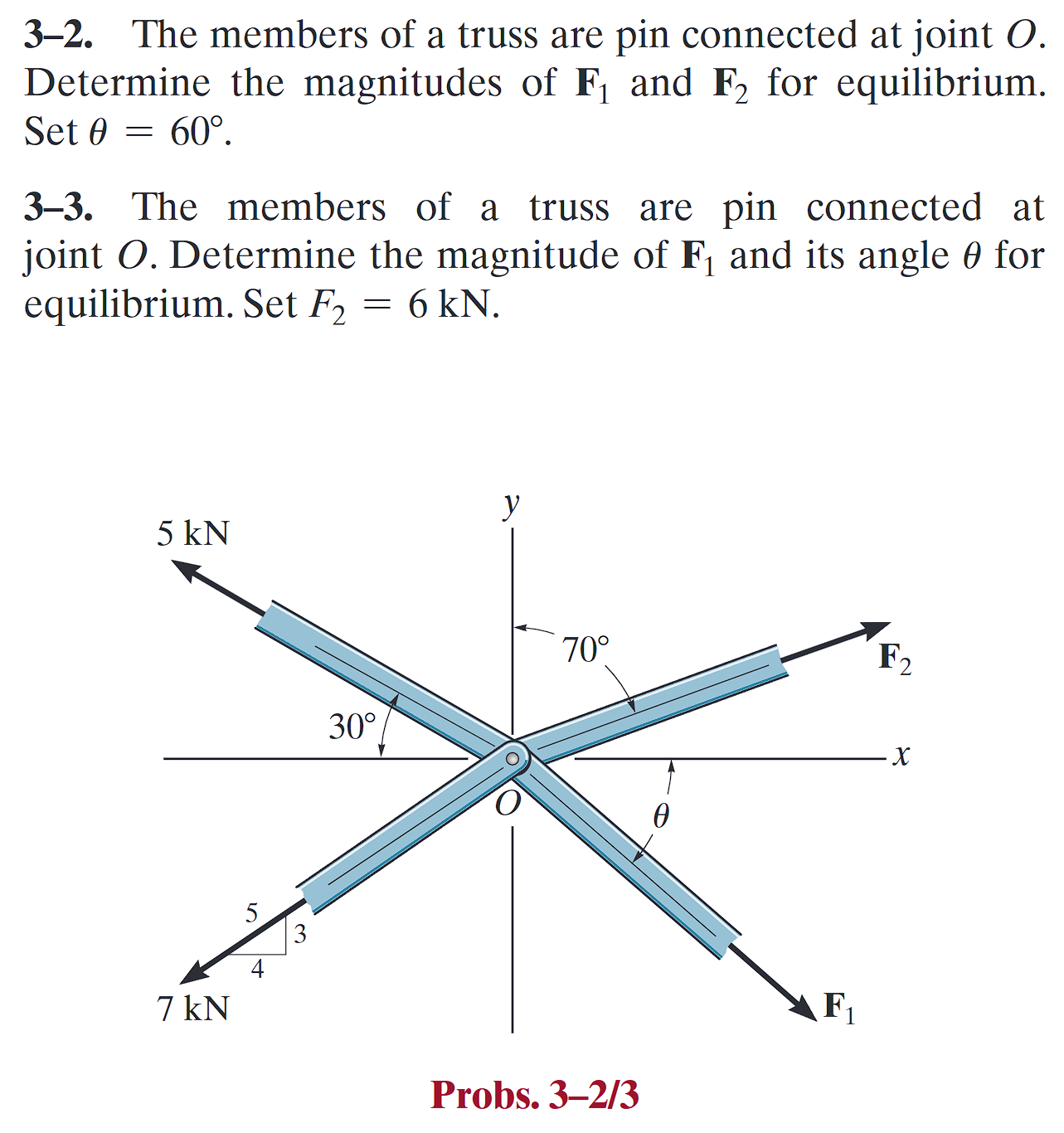
Probs. 3-2/3

Probs. 3-2 (点击展开)

Python

# 使用 sympy 库来建立并求解方程
import sympy as sp

Python

# 示例 3-2: 质点平衡与未知力的求解（已知方向，未知大小）
#
# 问题描述：
# 四个共点力作用于一个质点，其中：
# - F₁ 和 F₂ 的方向已知，大小未知；
# - F₃ 和 F₄ 的大小与方向已知。
# 求：在质点保持静力平衡的条件下，F₁ 与 F₂ 的大小。
#
# 物理背景：
# 对于共点力系统（concurrent force system），质点处于静力平衡时，
# 合力为零，即：
#
#     F₁ + F₂ + F₃ + F₄ = 0
#
# 本代码使用 SymPy 构造二维向量表示各力，通过建立平衡方程组，
# 求解未知力 F₁ 与 F₂ 的大小。

F_1_magnitude = sp.symbols('F_1', real=True, positive=True)
F_1_direction = sp.rad(-60)
F_1 = F_1_magnitude * sp.Matrix([sp.cos(F_1_direction), sp.sin(F_1_direction)])

F_2_magnitude = sp.symbols('F_2', real=True, positive=True)
F_2_direction = sp.rad(20)
F_2 = F_2_magnitude * sp.Matrix([sp.cos(F_2_direction), sp.sin(F_2_direction)])

F_3_magnitude = 5e3
F_3_direction = sp.rad(150)
F_3 = F_3_magnitude * sp.Matrix([sp.cos(F_3_direction), sp.sin(F_3_direction)])

F_4_magnitude = 7e3
F_4_direction = sp.atan2(-3, -4)
F_4 = F_4_magnitude * sp.Matrix([sp.cos(F_4_direction), sp.sin(F_4_direction)])

F_R = F_1 + F_2 + F_3 + F_4

equation = sp.Eq(F_R, sp.Matrix([0, 0]))
solution = sp.solve(equation, [F_1_magnitude, F_2_magnitude], dict=True)
print(f"F_1 = {float(solution[0][F_1_magnitude]):.3g} N, F_2 = {float(solution[0][F_2_magnitude]):.3g} N.")

输出：

F_1 = 1.83e+03 N, F_2 = 9.6e+03 N.

Probs. 3-3 (点击展开)

Python

# 示例 3-3: 质点平衡与未知力的求解（已知大小，未知方向）
#
# 问题描述：
# 四个共点力作用于一个质点，其中：
# - F₁ 的大小与方向均未知；
# - F₂、F₃、F₄ 的大小与方向均已知。
# 求：在质点保持静力平衡的条件下，F₁ 的大小与方向。
#
# 解题思路：
# - 用方向余弦与正弦（cosθ, sinθ）表示 F₁ 的方向分量，
#   这样做是为了避免直接用 θ 作为未知数时，因包含非线性的三角函数导致方程难以求解；
#   直接以 cosθ 和 sinθ 作为未知数可以将问题转化为线性方程组，
#   从而利用线性代数方法快速求解；
# - 根据平衡条件：
#
#       F₁ + F₂ + F₃ + F₄ = 0
#
#   分别列出 x、y 分量的平衡方程；
# - 加上单位向量约束：
#
#       cos²θ + sin²θ = 1
#
#   构成三元一次方程组，解出 F₁ 的大小和方向；
# - 最后使用 atan2 函数还原方向角 θ。

F_1_magnitude = sp.symbols('F_1', real=True, positive=True)
F_1_direction_cosine = sp.symbols('F_1_direction_cosine', real=True)
F_1_direction_sine = sp.symbols('F_1_direction_sine', real=True)
F_1 = F_1_magnitude * sp.Matrix([F_1_direction_cosine, F_1_direction_sine])

F_2_magnitude = 6e3
F_2_direction = sp.rad(20)
F_2 = F_2_magnitude * sp.Matrix([sp.cos(F_2_direction), sp.sin(F_2_direction)])

F_3_magnitude = 5e3
F_3_direction = sp.rad(150)
F_3 = F_3_magnitude * sp.Matrix([sp.cos(F_3_direction), sp.sin(F_3_direction)])

F_4_magnitude = 7e3
F_4_direction = sp.atan2(-3, -4)
F_4 = F_4_magnitude * sp.Matrix([sp.cos(F_4_direction), sp.sin(F_4_direction)])

F_R = F_1 + F_2 + F_3 + F_4

equation_1 = sp.Eq(F_R[0], 0)
equation_2 = sp.Eq(F_R[1], 0)
equation_3 = sp.Eq(F_1_direction_cosine**2 + F_1_direction_sine**2, 1)
solution = sp.solve([(]equation_1, equation_2, equation_3], [F_1_magnitude, F_1_direction_cosine, F_1_direction_sine], dict=True)

θ = sp.atan2(solution[0][F_1_direction_sine], solution[0][F_1_direction_cosine])
print(f"F_1 = {float(solution[0][F_1_magnitude]):.3g} N, F_θ = {float(sp.deg(θ)):.3g} deg.")

输出：

F_1 = 4.31e+03 N, F_θ = -4.69 deg.

平面受力分析 2

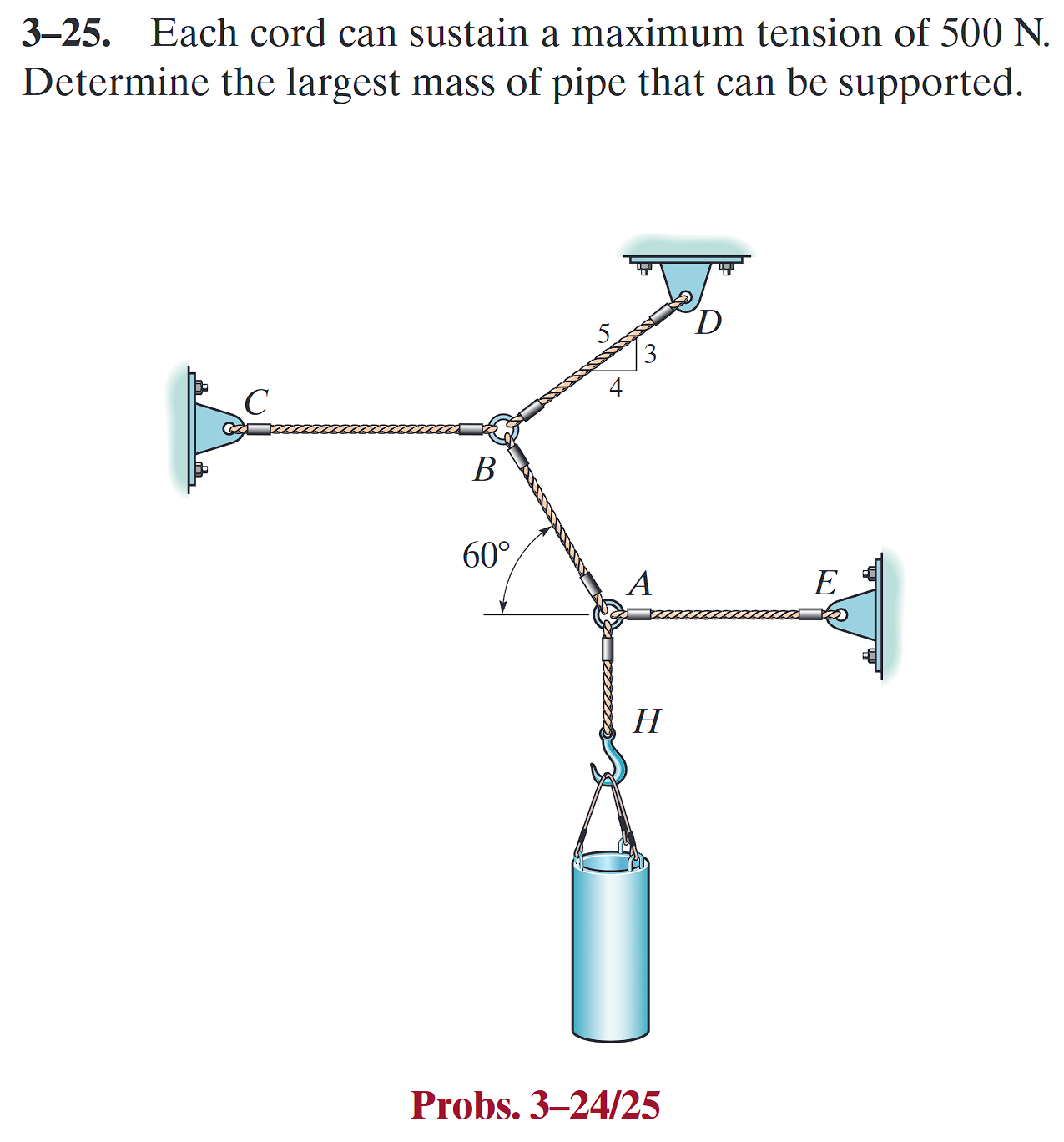
Probs. 3-24/25

Probs. 3-25 (点击展开)

Python

# 3-25.

import sympy as sp
from IPython.display import display, Math

# 定义未知质量 m 和最大允许拉力 tension_max
m = sp.symbols('m', real=True, positive=True)
tension_max = 500

# 定义各方向的单位向量
u_AB = sp.Matrix([sp.cos(sp.rad(120)), sp.sin(sp.rad(120))])  # AB 杆方向
u_AE = sp.Matrix([1, 0])                                     # AE 杆方向（水平向右）
u_AH = sp.Matrix([0, -1])                                    # AH 杆方向（竖直向下）

# 定义 A 点各杆的拉力大小（未知量），以及重力
F_AB_magnitude = sp.symbols('F_AB', real=True, positive=True)
F_AE_magnitude = sp.symbols('F_AE', real=True, positive=True)
F_AH_magnitude = m * 9.8  # A 点的重力

# 计算 A 点各杆的力矢量
F_AB = F_AB_magnitude * u_AB
F_AE = F_AE_magnitude * u_AE
F_AH = F_AH_magnitude * u_AH

# A 点受力平衡方程
F_A = F_AB + F_AE + F_AH

# 解 A 点平衡方程，得到 F_AB 和 F_AE 关于 m 的表达式
equations = [
    sp.Eq(F_A[0], 0),
    sp.Eq(F_A[1], 0)
]
solution = sp.solve(equations, [F_AB_magnitude, F_AE_magnitude], dict=True)

F_AB_magnitude = solution[0][F_AB_magnitude]
F_AE_magnitude = solution[0][F_AE_magnitude]
F_AB = F_AB_magnitude * u_AB
F_AE = F_AE_magnitude * u_AE

# 定义 B 点各杆的单位向量
u_BA = -u_AB  # BA 方向与 AB 相反
u_BC = sp.Matrix([-1, 0])  # BC 杆方向（水平向左）
u_BD = sp.Matrix([sp.cos(sp.atan2(3, 4)), sp.sin(sp.atan2(3, 4))])  # BD 杆方向

# B 点各杆的拉力大小
F_BA_magnitude = F_AB_magnitude  # BA 与 AB 拉力大小相等
F_BC_magnitude = sp.symbols('F_BC', real=True, positive=True)
F_BD_magnitude = sp.symbols('F_BD', real=True, positive=True)

# 计算 B 点各杆的力矢量
F_BA = F_BA_magnitude * u_BA
F_BC = F_BC_magnitude * u_BC
F_BD = F_BD_magnitude * u_BD

# B 点受力平衡方程
F_B = F_BA + F_BC + F_BD

# 解 B 点平衡方程，得到 F_BC 和 F_BD 关于 m 的表达式
equations = [
    sp.Eq(F_B[0], 0),
    sp.Eq(F_B[1], 0)
]
solution = sp.solve(equations, [F_BC_magnitude, F_BD_magnitude], dict=True)

F_BC_magnitude = solution[0][F_BC_magnitude]
F_BD_magnitude = solution[0][F_BD_magnitude]
F_BC = F_BC_magnitude * u_BC
F_BD = F_BD_magnitude * u_BD

# 以各杆拉力等于最大允许拉力为约束，分别解出对应的 m
equations = [
    sp.Eq(F_AB.norm(), tension_max),
    sp.Eq(F_AE.norm(), tension_max),
    sp.Eq(F_AH.norm(), tension_max),
    sp.Eq(F_BC.norm(), tension_max),
    sp.Eq(F_BD.norm(), tension_max)
]
m_values = []
for eq in equations:
    sol = sp.solve(eq, m, dict=True)
    if sol:
        m_values.append(sol[0][m])
# 取所有约束下的最小 m，作为系统最大允许质量
m_max = min(m_values)
print(f"m_max = {float(m_max):.3g} kg.")

输出：

m_max = 26.7 kg.

三维受力分析

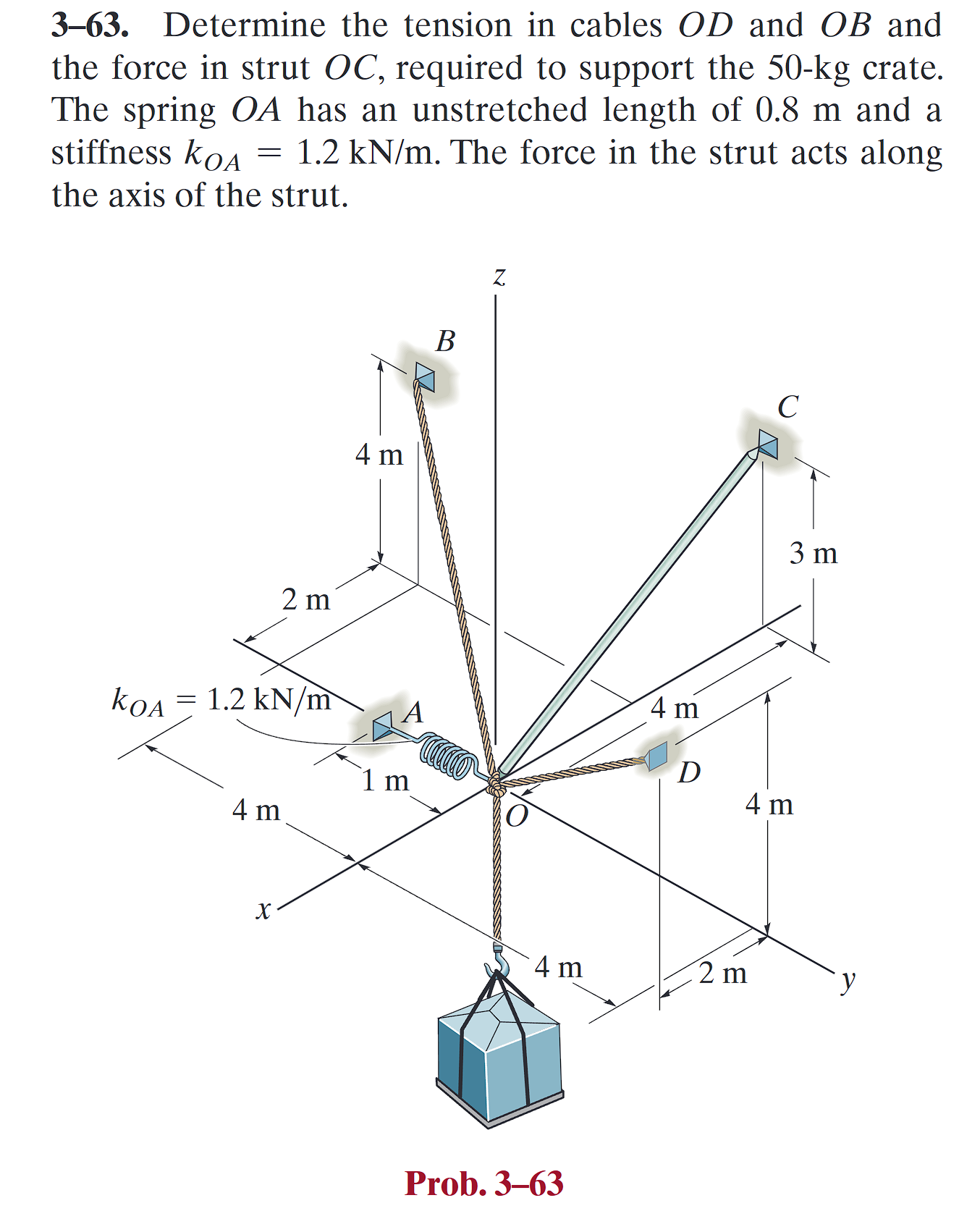
Prob. 3-63

Probs. 3-63 (点击展开)

Python

# 3-63.
import sympy as sp

# 设定物体质量和重力加速度
m, g = 50, 9.8
# 设定弹簧的初始和当前长度，以及弹簧常数
L_OA_0 = 0.8
L_OA = 1
k_OA = 1.2e3

# 设定各个点的坐标
point_O = sp.Matrix([0, 0, 0])
point_A = sp.Matrix([0, -1, 0])
point_B = sp.Matrix([-2, -4, 4])
point_C = sp.Matrix([-4, 0, 3])
point_D = sp.Matrix([2, 4, 4])
point_crate = point_O + sp.Matrix([0, 0, -1]) # 假设物体在点 O 正下方 1 米处

# 设定各个力的单位向量
unit_vector_OA = (point_A - point_O).normalized()
unit_vector_OB = (point_B - point_O).normalized()
unit_vector_OC = (point_C - point_O).normalized()
unit_vector_OD = (point_D - point_O).normalized()
unit_vector_crate = (point_crate - point_O).normalized()

# 设定各个力的大小
F_OA_magnitude = k_OA * (L_OA - L_OA_0)
F_OB_magnitude = sp.symbols('F_OB', real=True, positive=True)
F_OC_magnitude = sp.symbols('F_OC', real=True, positive=True)
F_OD_magnitude = sp.symbols('F_OD', real=True, positive=True)
F_crate_magnitude = m * g

# 计算力向量
F_OA_vector = F_OA_magnitude * unit_vector_OA
F_OB_vector = F_OB_magnitude * unit_vector_OB
F_OC_vector = F_OC_magnitude * unit_vector_OC
F_OD_vector = F_OD_magnitude * unit_vector_OD
F_crate_vector = F_crate_magnitude * unit_vector_crate

# 计算合力向量
F_resultant_vector = F_OA_vector + F_OB_vector + F_OC_vector + F_OD_vector + F_crate_vector

# 设定平衡方程 (三维力平衡)
equations = [
    sp.Eq(F_resultant_vector[0], 0),
    sp.Eq(F_resultant_vector[1], 0),
    sp.Eq(F_resultant_vector[2], 0)
]
# 求解方程组
solution = sp.solve(equations, [F_OB_magnitude, F_OC_magnitude, F_OD_magnitude], dict=True)
# 打印结果
print(f"F_OB = {float(solution[0][F_OB_magnitude]):.3g} N")
print(f"F_OC = {float(solution[0][F_OC_magnitude]):.3g} N")
print(f"F_OD = {float(solution[0][F_OD_magnitude]):.3g} N")

输出：

F_OB = 120 N
F_OC = 150 N
F_OD = 480 N

质点的平衡 ​

质点的平衡公式 ​

二维空间 ​

三维空间 ​

示例 ​

平面受力分析 1 ​

平面受力分析 2 ​

三维受力分析 ​

质点的平衡

质点的平衡公式

二维空间

三维空间

示例

平面受力分析 1

平面受力分析 2

三维受力分析