重心和质心
Center of Gravity and Centroid
形心 (centroid) 和质心 (center of mass) 会精确地重合在一起,如果物体的质量分布均匀(即物体的密度为常数)。文本只涉及质量分布均匀的物体,所以本文中对形心和质心不做细致地分辨。
基本公式
重心坐标的计算公式:
质心坐标的计算公式:
其中,
复合体
Composite Bodies
一、核心思想
计算一个复杂形状物体(复合体)的质心时,我们无需直接对其进行复杂的积分运算。核心思想是化整为零,再合零为:
分解 (化整为零):将复杂的复合体分解成若干个形状规则、质心位置已知的简单几何体(如矩形、三角形、圆、立方体、圆柱体等)的组合。
加权平均 (合零为整):将每个简单几何体视为一个质点,其质量(或体积、面积)集中在其各自的质心上。整个复合体的质心,就是这些“质点”的加权平均位置。
这个方法将一个微积分问题简化为了一个基础的代数和算术问题。
二、计算步骤
选择坐标系:建立一个合适的笛卡尔坐标系 (x, y, z)。
分解物体:将复合体分解成有限个简单的几何部分。
列表分析:创建一个表格,列出每个简单部分的以下信息:
质量
(如果密度均匀,则为体积 或面积 )。 各自的质心坐标
。
应用公式:使用加权平均公式计算整个复合体的质心坐标
。
三、计算公式
假设一个复合体由
总质量 (M):
复合体质心坐标 (
注意:对于密度均匀的物体,可以将质量
帕普斯-古尔丁努斯定理
Theorems of Pappus and Guldinus
该定理提供了一种计算旋转体表面积和体积的简便方法,其核心是将复杂的积分运算简化为质心的几何路径计算。
帕普斯 (Pappus, 古希腊, 约 3 世纪) 和古尔丁努斯 (Guldinus, 瑞士, 16 世纪) 分别独立发现了这一定理。
第一定理:旋转曲面的面积
一个由生成曲线 (generating curve) 绕外部轴旋转任意角度
其中,
是生成的旋转曲面的面积。 是绕轴旋转的角度(弧度制)。 是生成曲线的质心到旋转轴的垂直距离。 是生成曲线的长度。
第二定理:旋转体的体积
一个由生成面 (generating surface) 绕外部轴旋转任意角度
其中,
是生成的旋转体的体积。 是绕轴旋转的角度(弧度制)。 是生成面的质心到旋转轴的垂直距离。 是生成面的面积。
补充
- 旋转轴不能穿过生成曲线或生成面。
- 旋转角度
可以是任意值,不限于 。
应用于复合体
当生成曲线或面是由多个简单的部分组合而成时,无需计算整个复杂形状的总质心,而是可以分别计算每个部分的质心,然后使用加权平均的方法来确定整体的质心位置。
- 复合曲线生成的旋转曲面面积:
- 复合面生成的旋转体体积:
一般分布载荷的合力
Resultant of a General Distributed Loading
(综合应用)
流体压力
Fluid Pressure
(综合应用。注意一点,在静力学的范围内,在静止流体中,由流体压力产生的力,其方向永远与它所作用的任何表面相垂直。)
示例
Example 9.1
Locate the centroid of the rod bent into the shape of a parabolic arc as shown in Fig.9-8.
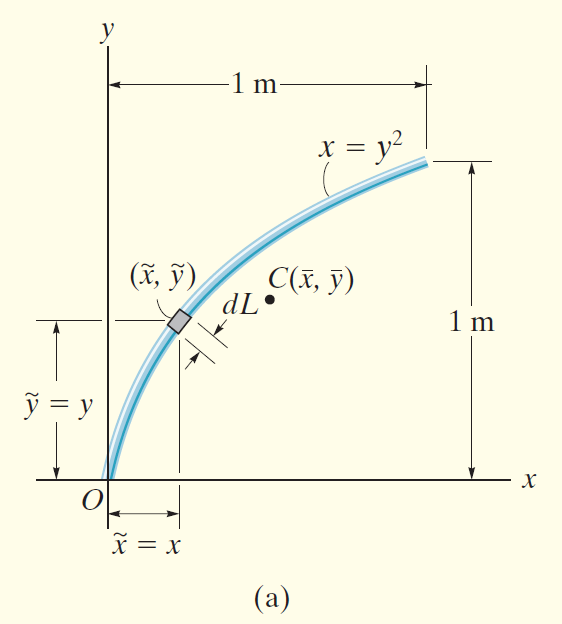
Solution
如图建系。假设杆的质量为
杆的形状可以用参数方程表示:
于是,
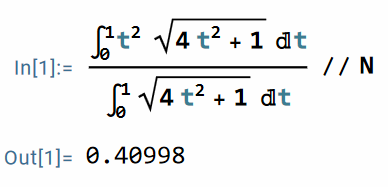
同理,
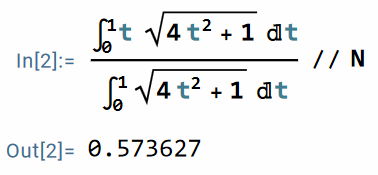
因此,此杆的质心坐标为 (0.410, 0.574)。
Example 9.2
Locate the centroid of the circular wire segment shown in Fig.9-9.
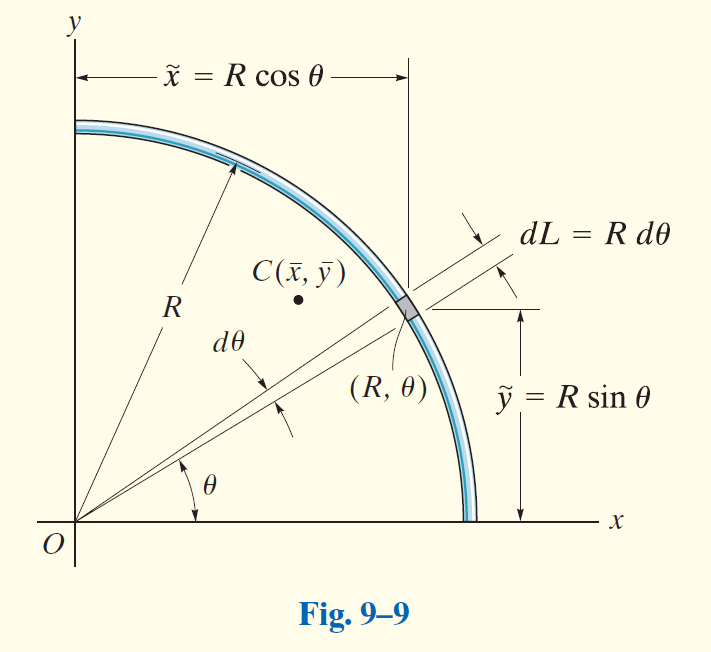
Solution
如图建系。假设圆形线段的质量为
该圆形线段可用参数方程表示为:
于是,
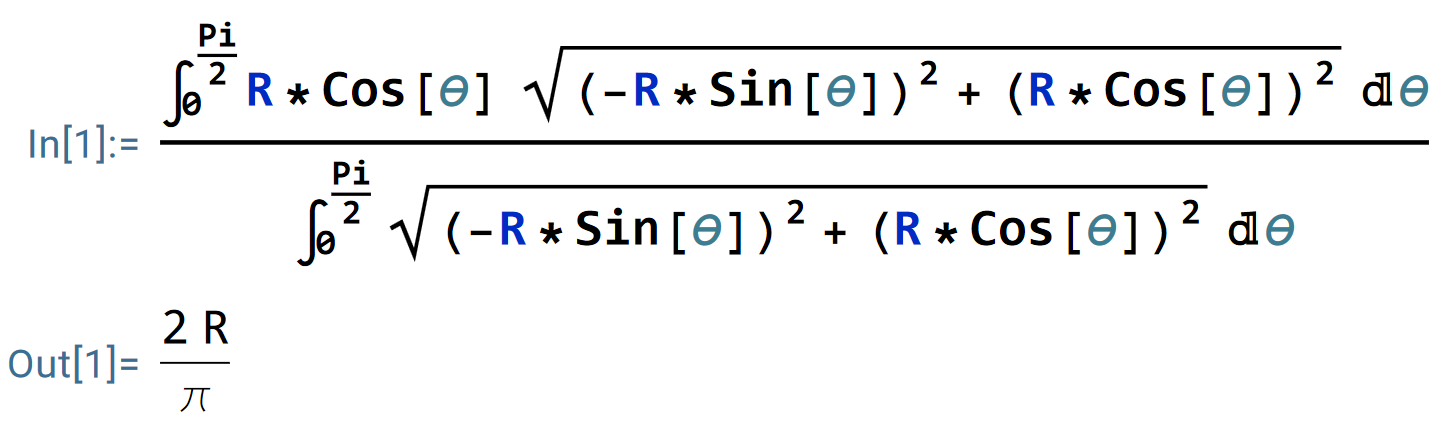
同理,
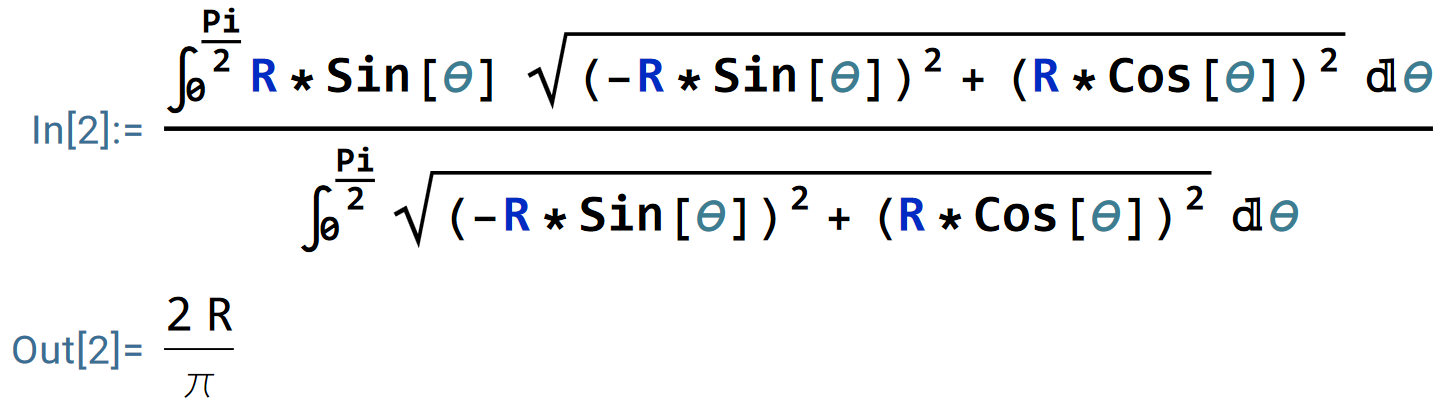
因此,此圆形线段的质心坐标为 (
Example 9.3
Determine the distance
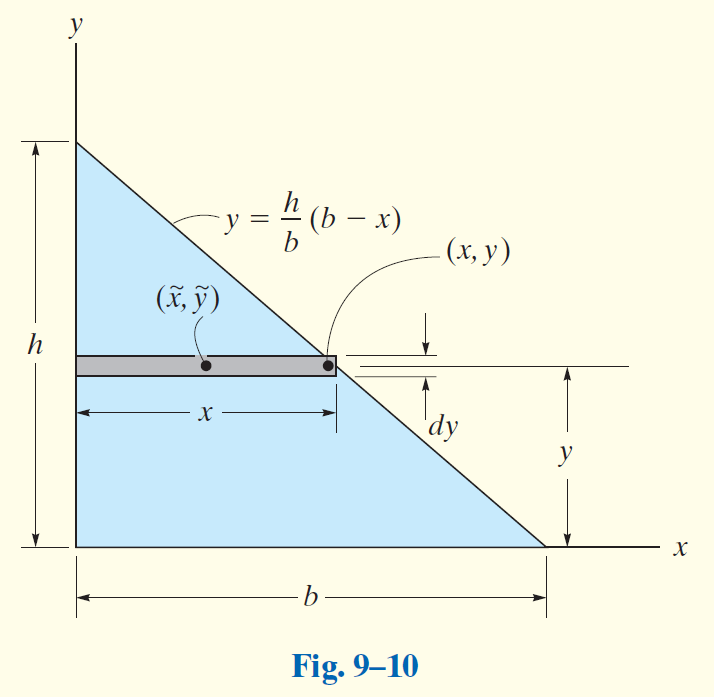
Solution
如图建系。假设该三角形的重量为
该三角形的边界可以表示为:
于是,
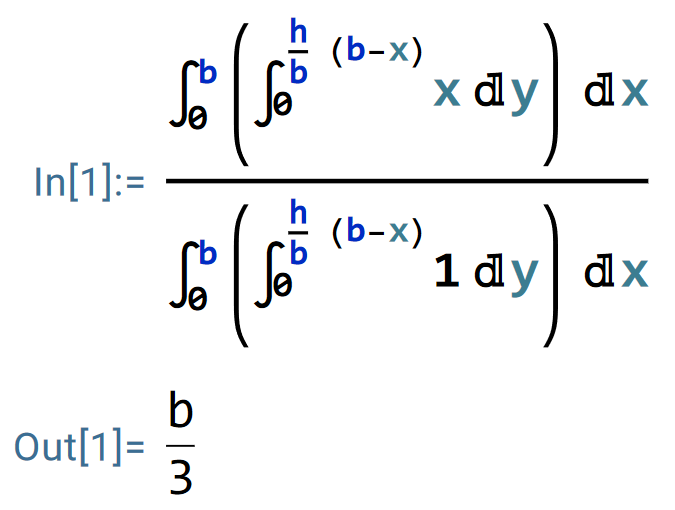
同理,
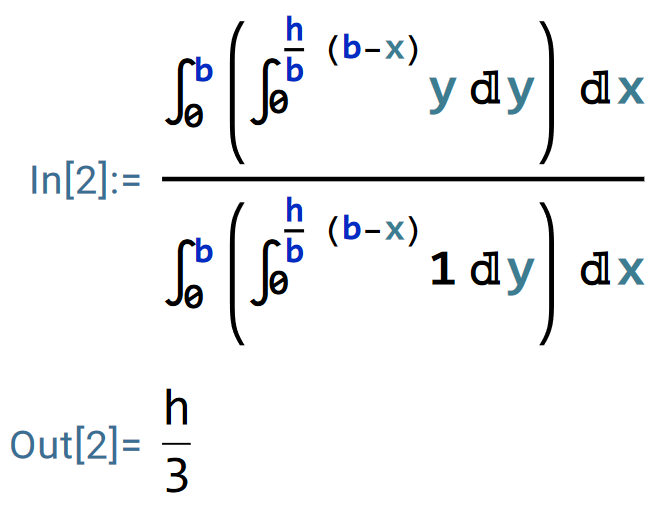
因此,此三角形的质心坐标为 (
Example 9.4
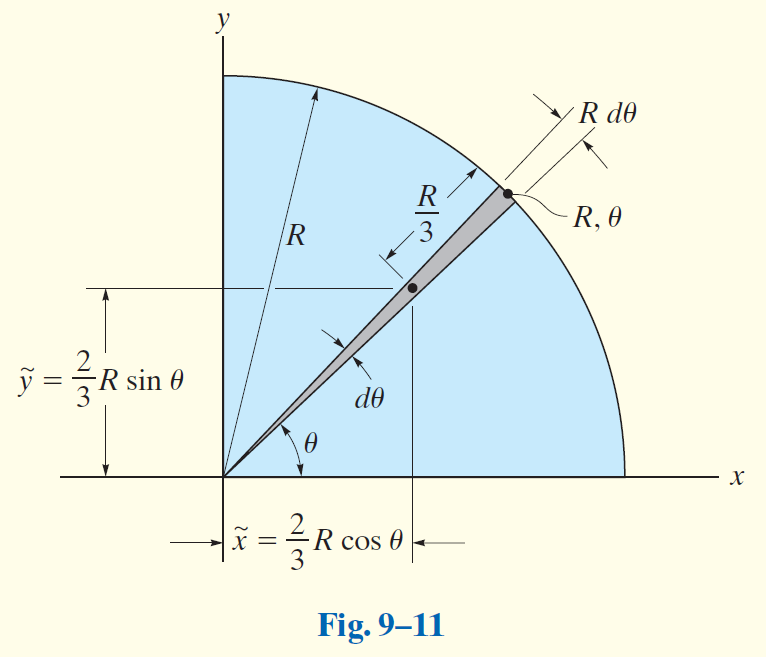
Locate the centroid of the area of a quarter circle shown in Fig.9-11.
Solution
如图建系。假设该四分之一圆的重量为
该四分之一圆的参数方程为:
于是,
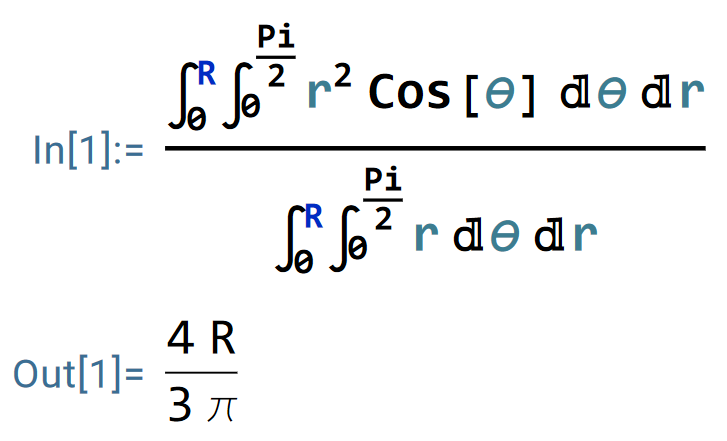
同理,
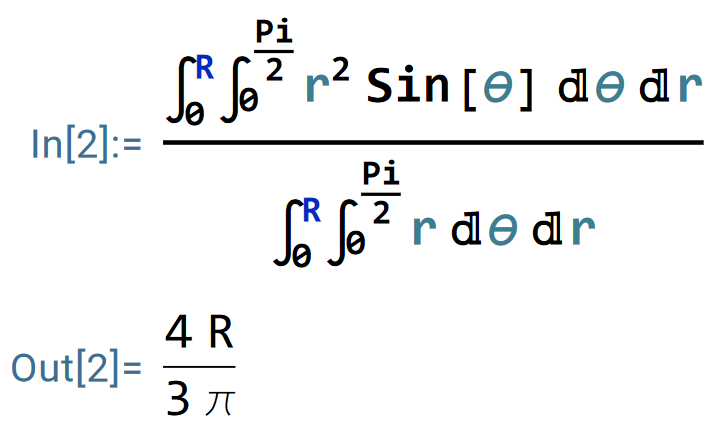
因此,此四分之一圆的质心坐标为
Example 9.5
Locate the centroid of the area of shown in Fig.9-12.
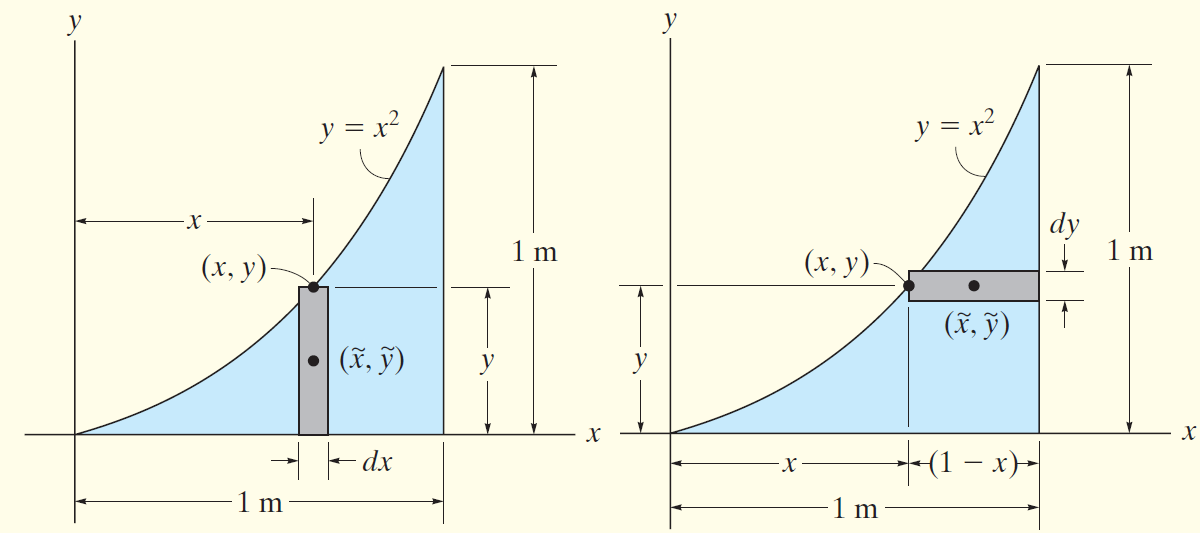
Solution
如图建系。
该图形的边界可以表示为:
于是,
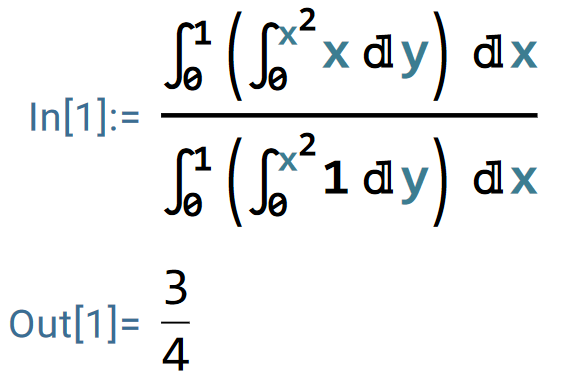
同理,
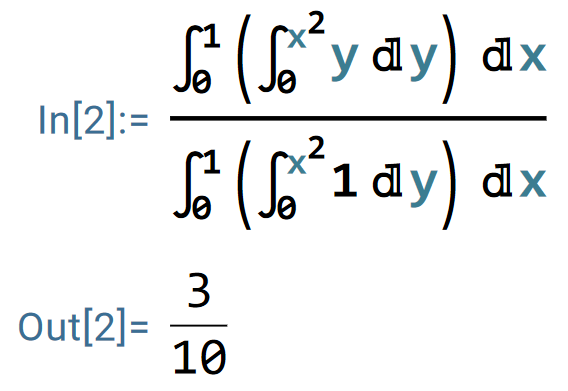
因此,此图形的质心坐标为 (
Example 9.6
Locate the centroid of the semi-elliptical area shown in Fig.9-13.
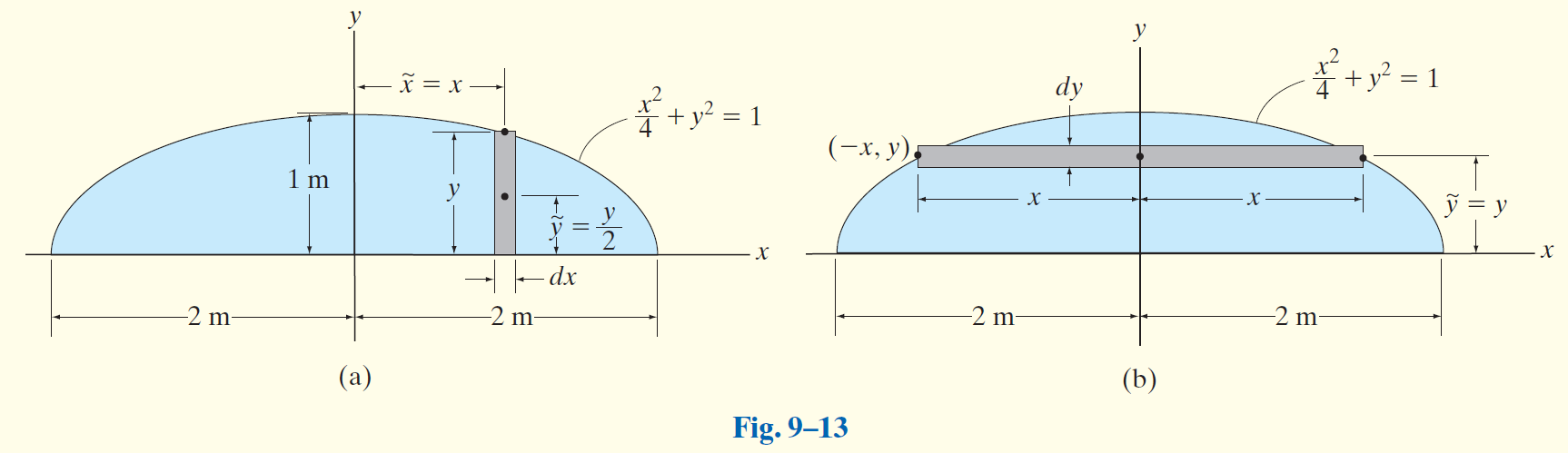
Solution
如图建系。
该半椭圆的边界可以表示为:
于是,
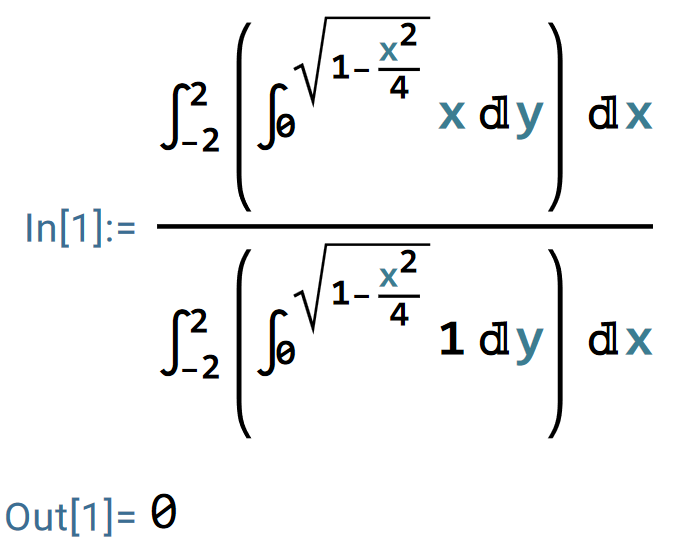
同理,
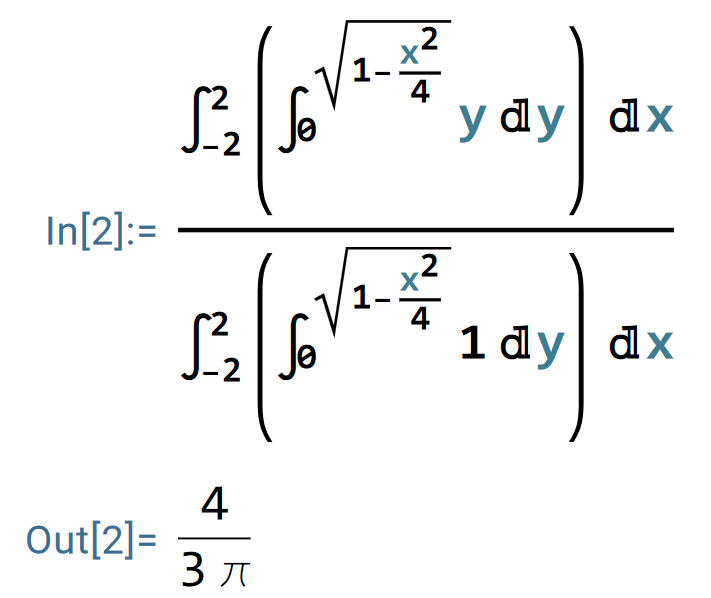
因此,此半椭圆的质心坐标为 (0,
Example 9.7
Locate the
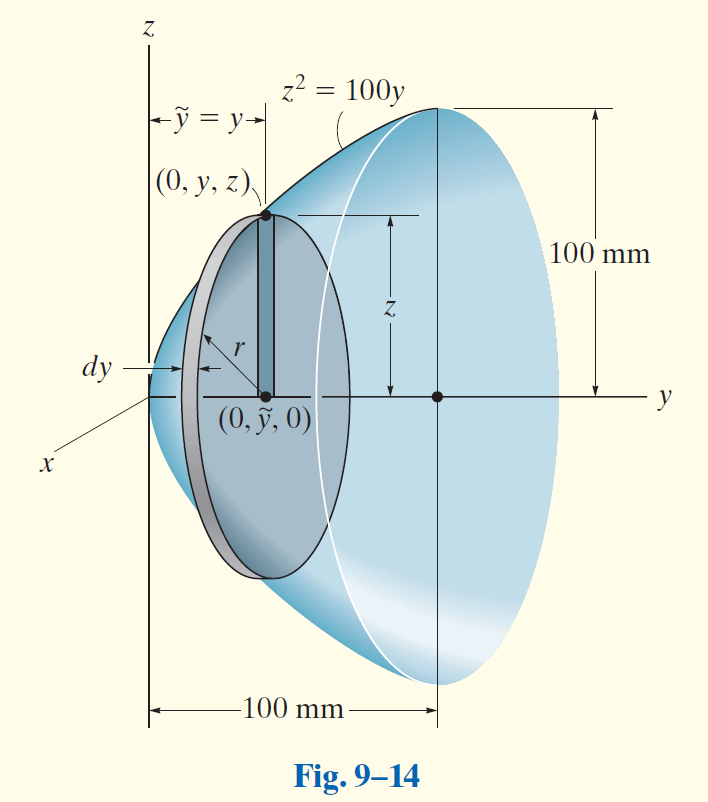
Solution
如图建系。
该抛物体可以表示为:
圆柱坐标系下:
体积积分单元:
于是,

因此,此抛物体的质心坐标为 (0, 66.67, 0) mm。
Example 9.8
Determine the location of the center of mass of the cylinder shown in Fig.9-15 if its density varies directly with the distance from its base, i.e.,
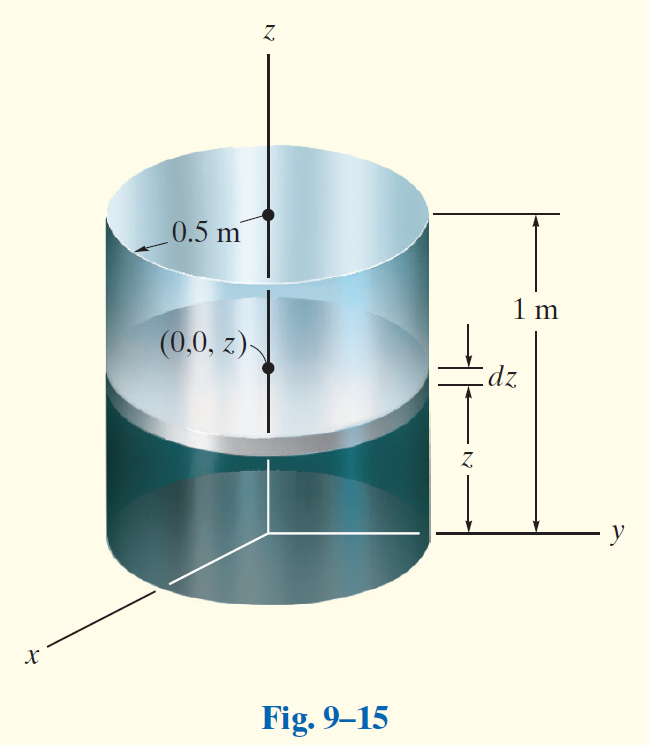
Solution
如图建系。这是一个标准的圆柱体,底面半径
于是,

因此,此圆柱体的重心坐标为 (0, 0, 0.667) m。
Problem 9.115
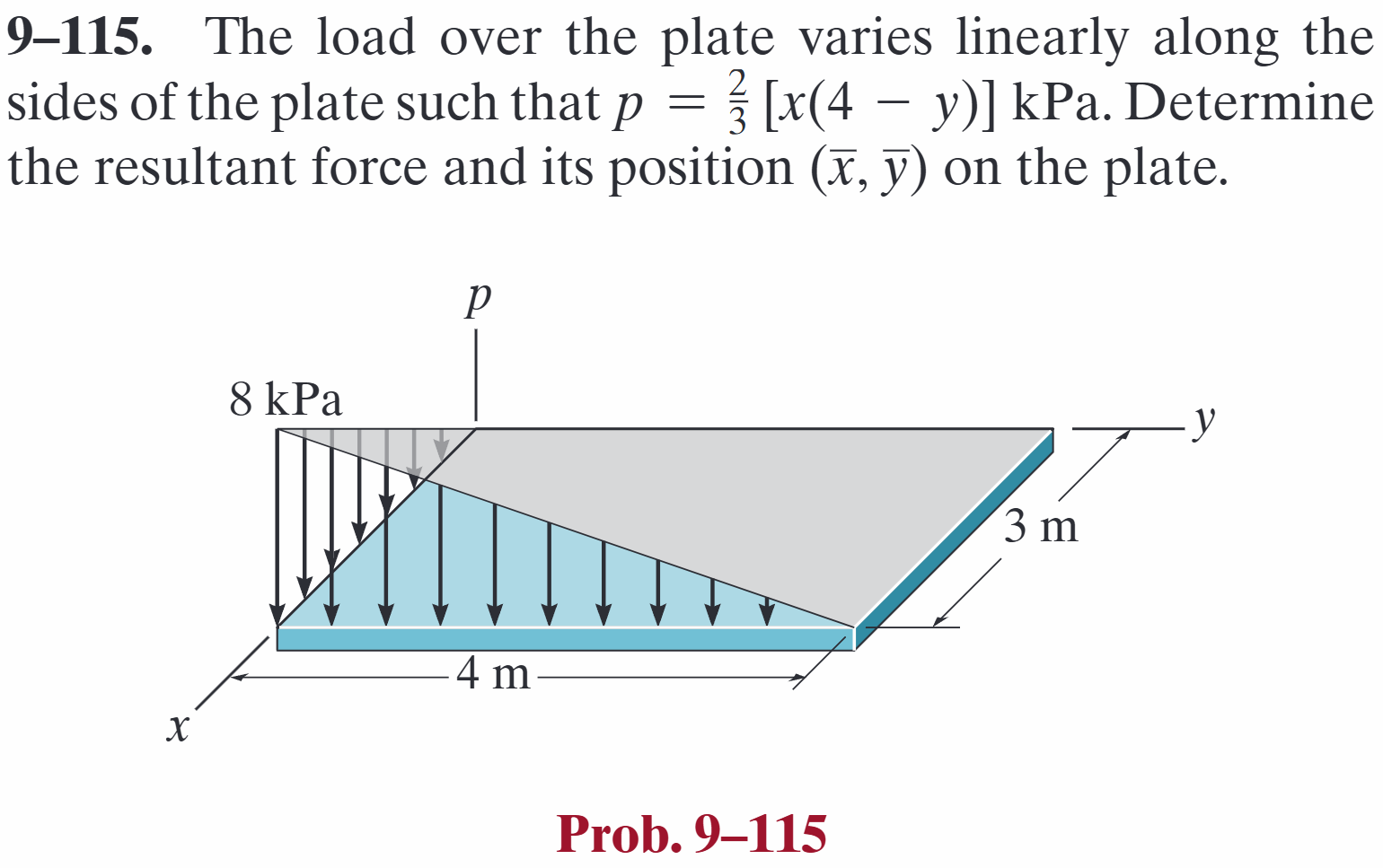
Solution

