一阶电路

First-Order Circuits

A first-order circuit is characterized by a first-order differential equation.

无源 RC 电路

The Source-Free RC Circuit

The natural response of a circuit refers to the behavior ( in terms of voltages and currents) of the circuit itself, with no external sources of excitation.

The time constant of a circuit is the time required for the response to decay to a factor of 1/e or 36.8% of its initial value.

$$\begin{array}{rl}\tau & =RC\\ v(t)& =V_0{e}^{-t/\tau }\end{array}$$

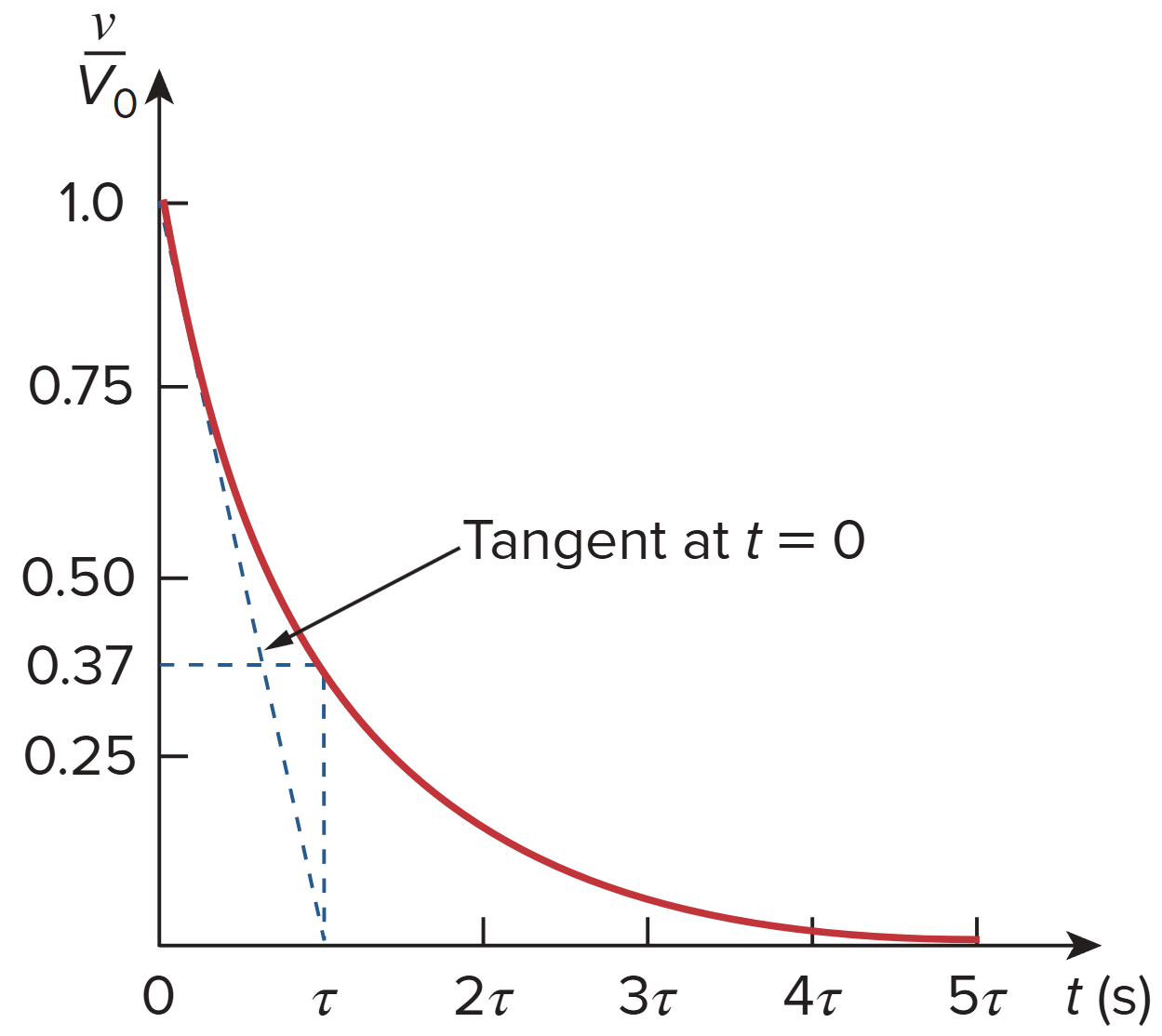
无源 RL 电路

The Source-Free RL Circuit

$$\begin{array}{rl}\tau & =L/R\\ i(t)& =I_0{e}^{-t/\tau }\end{array}$$

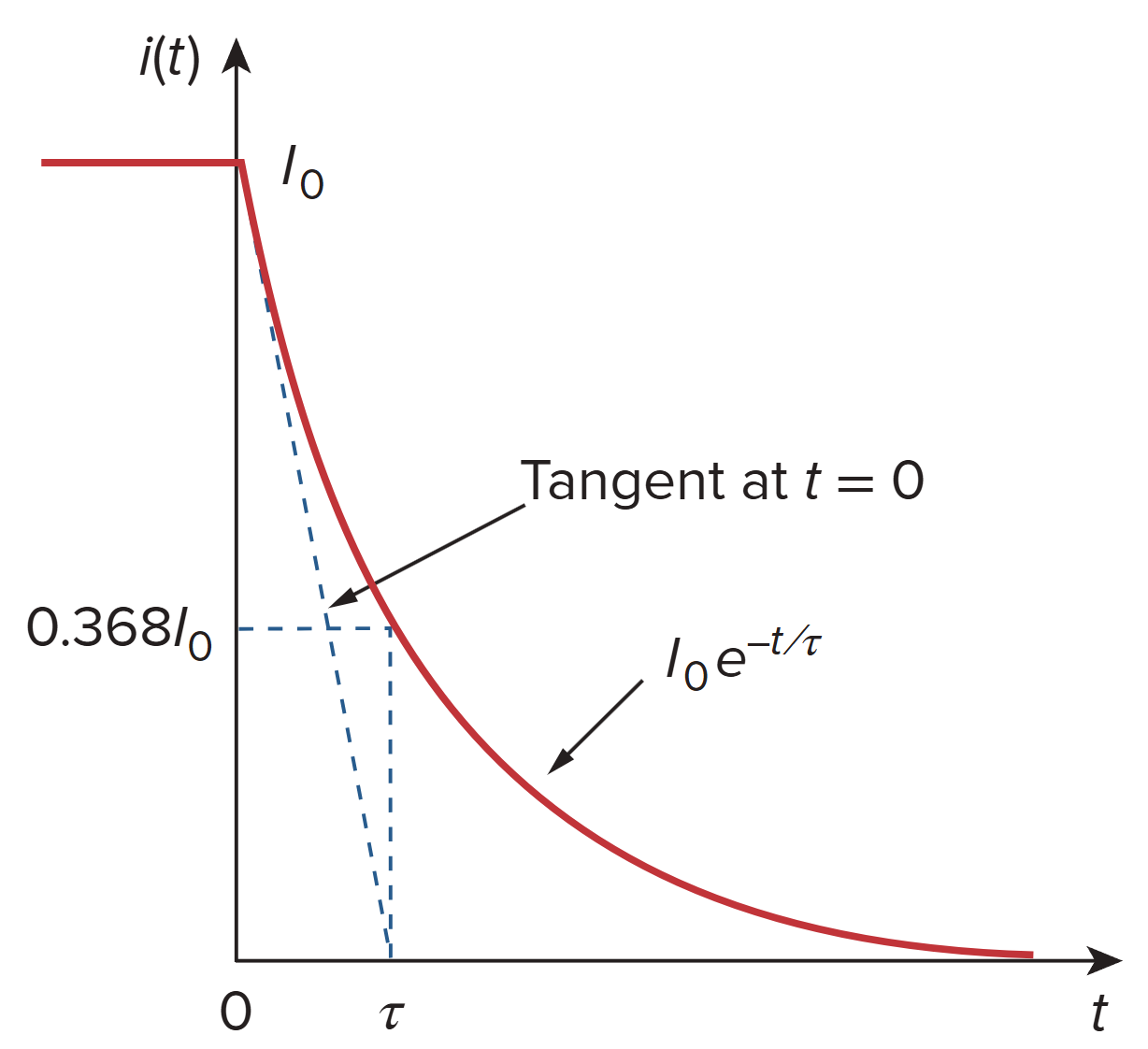
奇异函数

Singularity Functions

Singularity functions are functions that either are discontinuous or have discontinuous derivatives.

The unit step function u(t) is 0 for negative values of t and 1 for positive values of t.

$$u(t)=\{\begin{array}{ll}0,& t<0\\ 1,& t>0\end{array}$$

The unit impulse function δ(t) is zero everywhere except at t = 0, where it is undefined.

$$\delta (t)=\frac{\mathrm{d}}{\mathrm{d}t}u(t)=\{\begin{array}{ll}0,& t<0\\ \text{Undefined},& t=0\\ 0,& t>0\end{array}$$

重要性质：

$${\int }_{0^{-}}^{0^{+}}\delta (t)\mathrm{d}t=1$$$${\int }_a^{b}f(t)\delta (t-t_0)\mathrm{d}t=f(t_0)$$

The unit ramp function is zero for negative values of t and has a unit slope for positive values of t.

$$r(t)=\{\begin{array}{ll}0,& t\le 0\\ t,& t\ge 0\end{array}$$

这三个奇异函数之间通过微分和积分互相关联。

微分关系：

$$\frac{\mathrm{d}r(t)}{\mathrm{d}t}=u(t),\frac{\mathrm{d}u(t)}{\mathrm{d}t}=\delta (t).$$

积分关系：

$${\int }_{-\mathrm{\infty }}^t\delta (\lambda )\mathrm{d}\lambda =u(t),{\int }_{-\mathrm{\infty }}^{t}u(\lambda )\mathrm{d}\lambda =r(t).$$

RC 电路的阶跃响应

Step Response of an RC Circuit

The step response of a circuit is its behavior when the excitation is the step function, which may be a voltage or a current source.

$$v(t)=\{\begin{array}{ll}0,& t<0\\ V_s+(V_0-V_s)e^{-t/\tau },& t>0\end{array}$$

Complete Response

$$\boxed{{\displaystyle v(t)=v(\mathrm{\infty })+[v(t_0^{+})-v(\mathrm{\infty })]e^{-(t-t_0)/\tau }}}$$

RL 电路的阶跃响应

Step Response of an RL Circuit

$$i(t)=\{\begin{array}{ll}0,& t<0\\ I_s+(I_0-I_s)e^{-t/\tau },& t>0\end{array}$$

Complete Response

$$\boxed{{\displaystyle i(t)=i(\mathrm{\infty })+[i(t_0^{+})-i(\mathrm{\infty })]e^{-(t-t_0)/\tau }}}$$