磁耦合电路

Magnetically Coupled Circuits

互感系数

Mutual Inductance

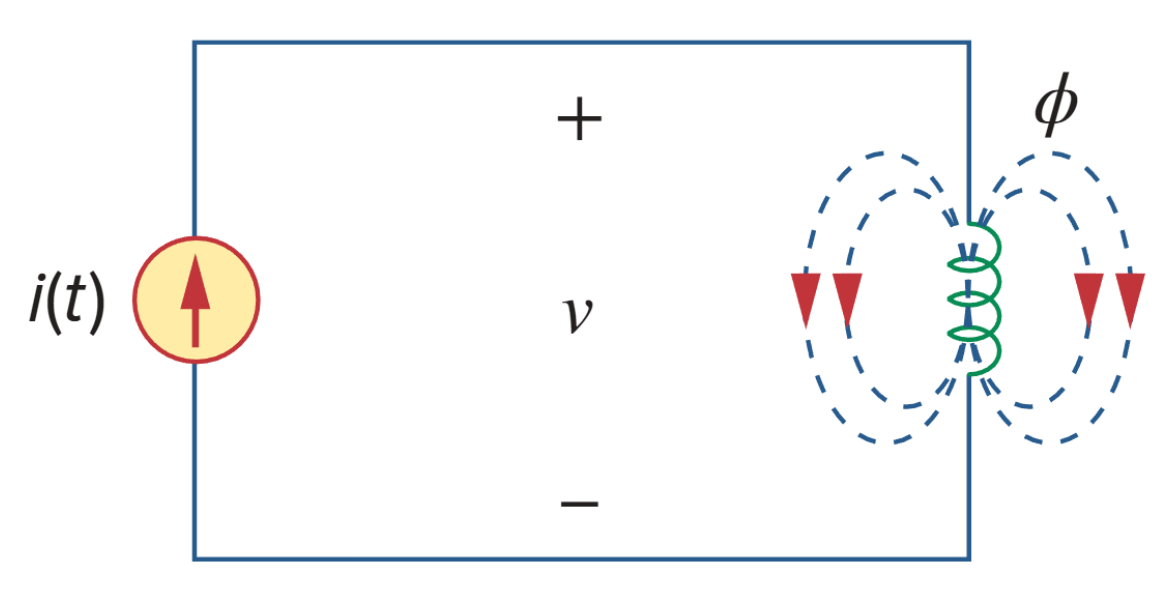
考虑这样的一个电感器，其线圈匝数为 N。当电流 i 流过线圈时，产生磁通量 ϕ。根据法拉第定律，产生的感应电压 v 与匝数 N 和磁通量 ϕ 对时间的变化率成正比：

$$v=N\frac{\mathrm{d}\varphi }{\mathrm{d}t}$$

由于磁通量来源于电流，因此磁通量的任何变化必然由电流的变化所致。由此，感应电压 v 还可以表达为：

$$\begin{array}{rl}v& =N\frac{\mathrm{d}\varphi }{\mathrm{d}i}\frac{\mathrm{d}i}{\mathrm{d}t}\\ & =L\frac{\mathrm{d}i}{\mathrm{d}t}\end{array}$$

其中，

$$L=N\frac{\mathrm{d}\varphi }{\mathrm{d}i}$$

被称为自感系数 (self-inductance)，其单位为亨利 (H)。

---

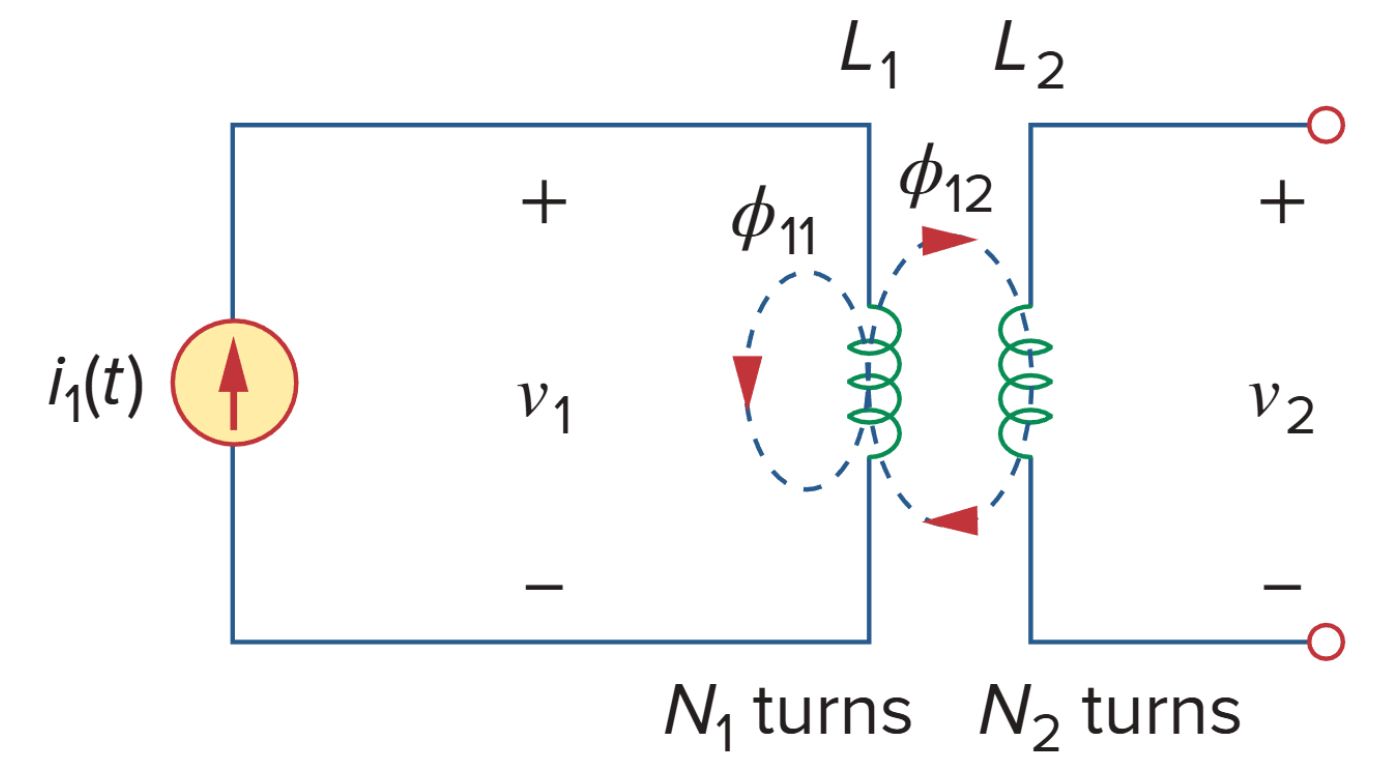
现在考虑两个自感量分别为 L₁ 和 L₂ 的线圈，它们彼此靠近。线圈 1 有 N₁ 匝，线圈 2 有 N₂ 匝。简单起见，假设第二个电感没有电流流过。来自线圈 1 的磁通量 ϕ₁ 具有两个分量：一个分量 ϕ₁₁ 仅链接线圈 1；另一个分量 ϕ₁₂ 链接线圈 1 和线圈 2。因此，

$${\varphi }_1={\varphi }_{11}+{\varphi }_{12}$$

尽管两个线圈之间物理上是分开的，但它们被称为磁耦合。由于整个磁通量 ϕ₁ 穿过线圈 1，因此线圈 1 的感应电压 v₁ 可以表示为：

$$v_1=N_1\frac{\mathrm{d}{\varphi }_1}{\mathrm{d}t}$$

由于只有磁通量 ϕ₁₂ 穿过线圈 2，因此线圈 2 的感应电压 v₂ 可以表示为：

$$v_2=N_2\frac{\mathrm{d}{\varphi }_{12}}{\mathrm{d}t}$$

继续，由于线圈 1 的磁通量 ϕ₁ 是由电流 i₁ 产生的，因此 v₁ 还可以表示为：

$$v_1=N_1\frac{\mathrm{d}{\varphi }_1}{\mathrm{d}{i}_1}\frac{\mathrm{d}{i}_1}{\mathrm{d}t}=L_1\frac{\mathrm{d}{i}_1}{\mathrm{d}t}$$

其中 $L_1=N_1{\displaystyle \frac{\mathrm{d}{\varphi }_1}{\mathrm{d}{i}_1}}$ 是线圈 1 的自感系数。
同理，线圈 2 的感应电压 v₂ 还可以表示为：

$$v_2=N_2\frac{\mathrm{d}{\varphi }_{12}}{\mathrm{d}{i}_1}\frac{\mathrm{d}{i}_1}{\mathrm{d}t}=M_{21}\frac{\mathrm{d}{i}_1}{\mathrm{d}t}$$

其中，

$$M_{21}=N_2\frac{\mathrm{d}{\varphi }_{12}}{\mathrm{d}{i}_1}$$

被称为线圈 2 关于线圈 1 的互感系数 (mutual inductance)，其单位为亨利 (H)。
因此，线圈 2 的开路互感电压 (open-circuit mutual voltage) 为：

$$\boxed{{\displaystyle v_2=M_{21}\frac{\mathrm{d}{i}_1}{\mathrm{d}t}}}$$

---

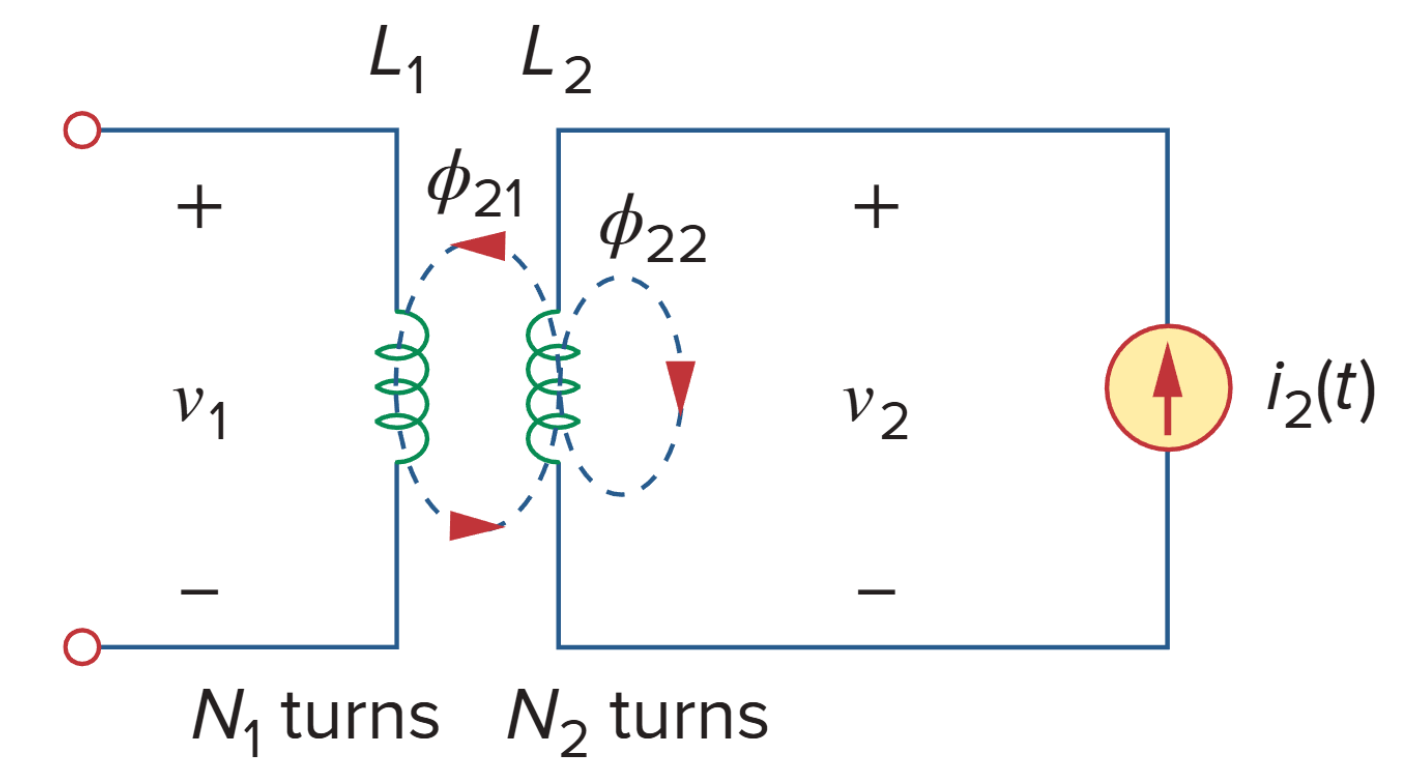
假设现在让电流 i₂ 流过线圈 2，而线圈 1 不带电。从线圈 2 流出的磁通量 ϕ₂ 也有两个分量：一个分量 ϕ₂₂ 仅链接线圈 2；另一个分量 ϕ₂₁ 链接线圈 2 和线圈 1。因此，

$${\varphi }_2={\varphi }_{22}+{\varphi }_{21}$$

由于整个磁通量 ϕ₂ 穿过线圈 2，因此线圈 2 的感应电压 v₂ 可以表示为：

$$v_2=N_2\frac{\mathrm{d}{\varphi }_2}{\mathrm{d}t}=N_2\frac{\mathrm{d}{\varphi }_2}{\mathrm{d}{i}_2}\frac{\mathrm{d}{i}_2}{\mathrm{d}t}=L_2\frac{\mathrm{d}{i}_2}{\mathrm{d}t}$$

由于只有磁通量 ϕ₂₁ 穿过线圈 1，因此线圈 1 的感应电压 v₁ 可以表示为：

$$v_1=N_1\frac{\mathrm{d}{\varphi }_{21}}{\mathrm{d}t}=N_1\frac{\mathrm{d}{\varphi }_{21}}{\mathrm{d}{i}_2}\frac{\mathrm{d}{i}_2}{\mathrm{d}t}=M_{12}\frac{\mathrm{d}{i}_2}{\mathrm{d}t}$$

其中，

$$M_{12}=N_1\frac{\mathrm{d}{\varphi }_{21}}{\mathrm{d}{i}_2}$$

为线圈 1 关于线圈 2 的互感系数。
因此，线圈 1 的开路互感电压 (open-circuit mutual voltage) 为：

$$\boxed{{\displaystyle v_1=M_{12}\frac{\mathrm{d}{i}_2}{\mathrm{d}t}}}$$

---

Mutual inductance is the ability of one inductor to induce a voltage across a neighboring inductor, measured in henrys (H).

互感定理

Reciprocity Theorem

The reciprocity theorem states that in a mutual inductance system, the mutual inductance between two coils is equal regardless of the direction of current through the coils. This means that if coil A induces a voltage in coil B when current flows through A, then the same current flowing through coil B will induce a voltage in coil A, demonstrating the symmetrical nature of inductive coupling.

$$M_{12}=M_{21}=M$$

点约定

Dot Convention

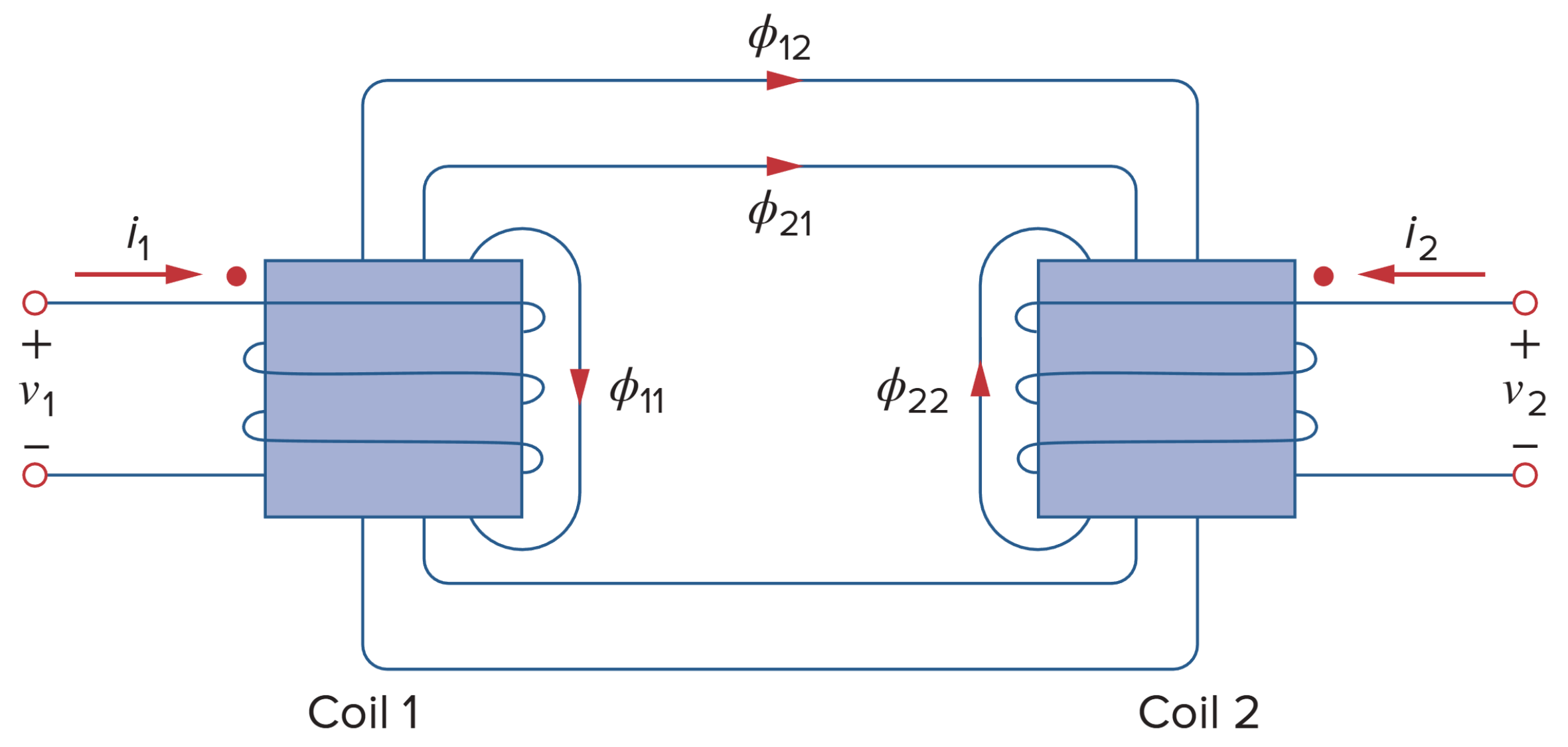
If a current enters the dotted terminal of one coil, the reference polarity of the mutual voltage in the second coil is positive at the dotted terminal of the second coil.

Alternatively,

If a current leaves the dotted terminal of one coil, the reference polarity of the mutual voltage in the second coil is negative at the dotted terminal of the second coil.

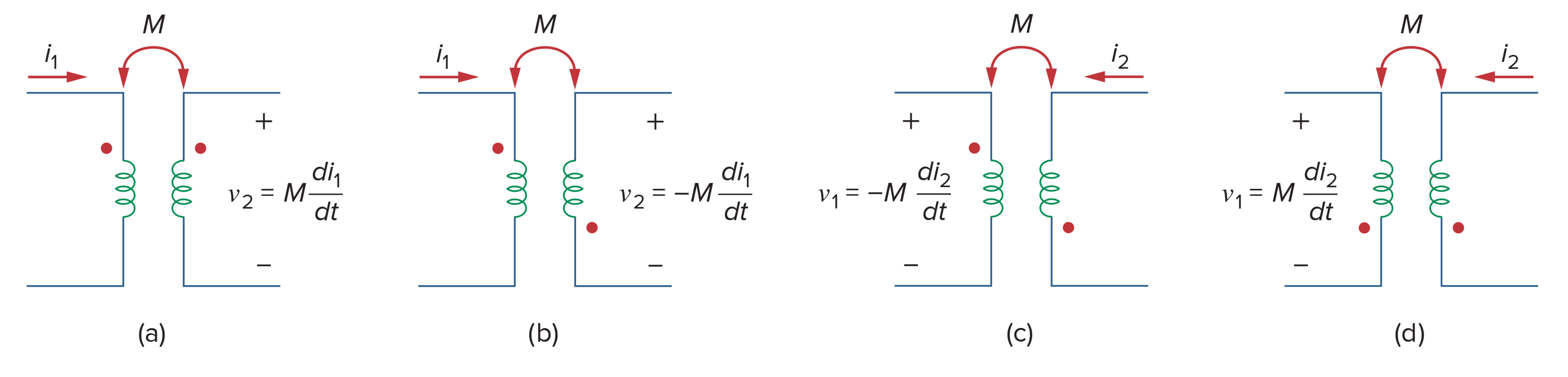
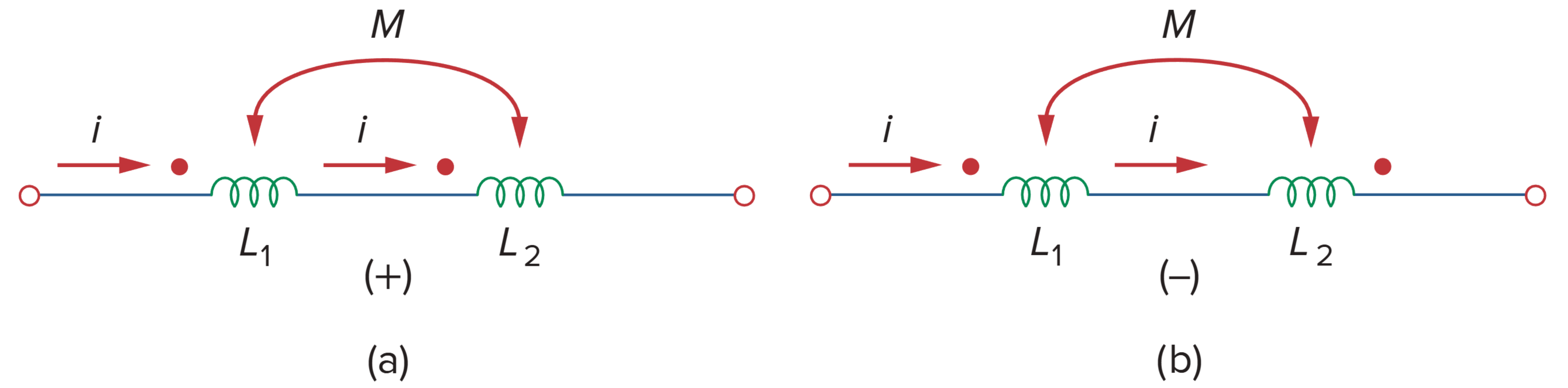
• Series-aiding connection:

$$L=L_1+L_2+2M$$

• Series-opposing connection:

$$L=L_1+L_2-2M$$

一个单独电感器的总电感 L 的真正构成是所有单匝的自感之和，再加上所有匝间互感的总和：

$$L=\sum _{i=1}^N{L}_i+2\sum _{i=1}^{N-1}\sum _{j=i+1}^N{M}_{ij}$$

耦合电路中的能量

Energy in a Coupled Circuits

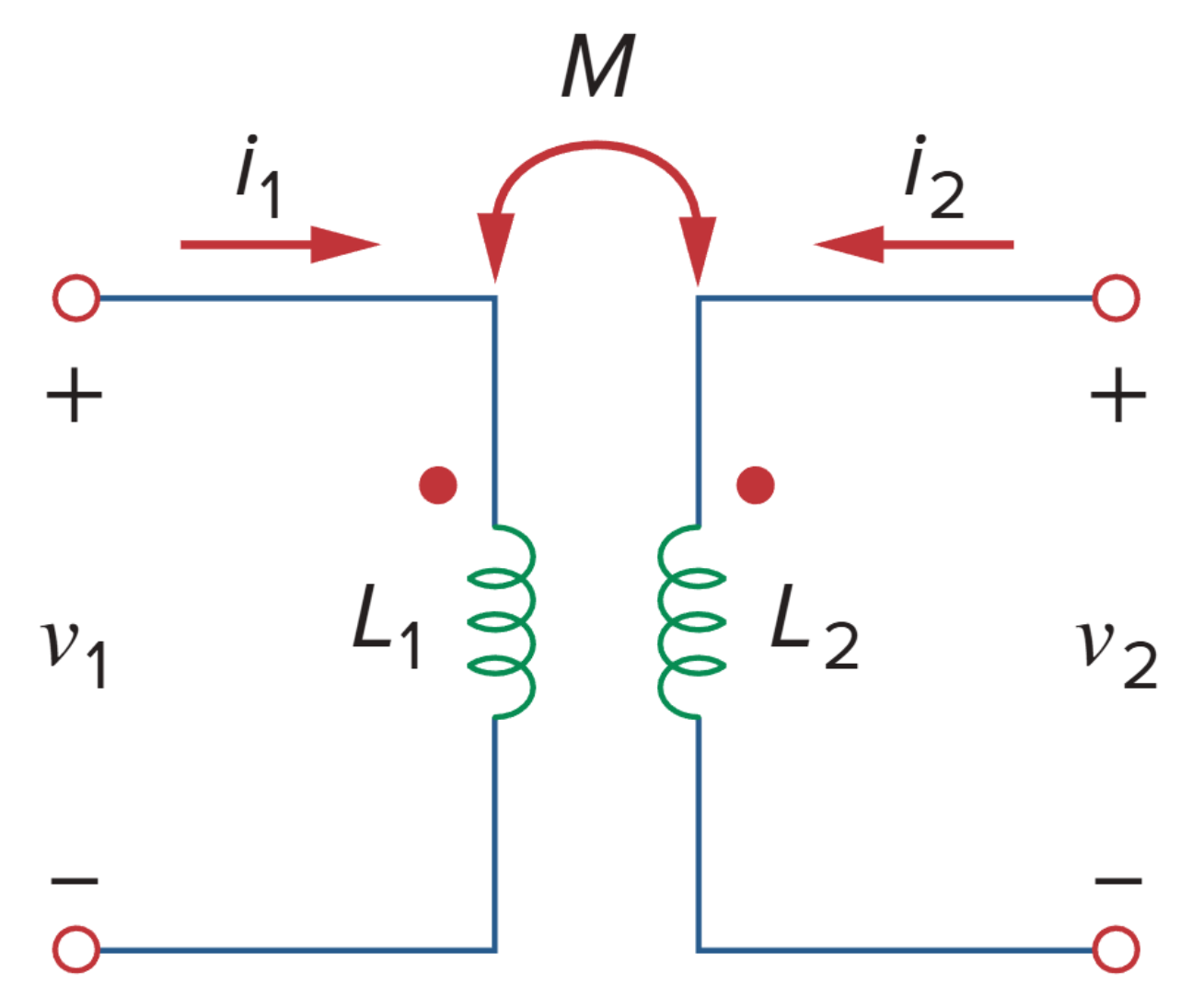
根据大学物理的结论，单独一个电感所能储存的最大能量为 $w=\frac{1}{2}L{i}^2$。

考虑如图所示的情况。假设电流 i₁ 和 i₂ 最初都为零，所以两个线圈中的能量也均为零。接下来，让电流 i₁ 从零开始增加到 I₁，同时电流 i₂ 保持为零。此时，线圈 1 中的瞬时功率为：

$$p_1(t)=v_1{i}_1=i_1{L}_1\frac{\mathrm{d}{i}_1}{\mathrm{d}t}$$

因此线圈 1 中的储存能量为：

$$w_1=\int p_1\mathrm{d}t=L_1{\int }_0^{I_1}{i}_1\mathrm{d}{i}_1=\frac{1}{2}{L}_1{I}_1^2$$

如果我们保持电流 i₁ 为 I₁，而让电流 i₂ 从零开始增加到 I₂，这个阶段下，两个线圈中的瞬时功率为：

$$p_2(t)=i_1{M}_{12}\frac{\mathrm{d}{i}_2}{\mathrm{d}t}+i_2{v}_2=I_1{M}_{12}\frac{\mathrm{d}{i}_2}{\mathrm{d}t}+i_2{L}_2\frac{\mathrm{d}{i}_2}{\mathrm{d}t}$$

阶段 2 的储存能量为：

$$\begin{array}{rl}{w}_2=\int p_2\mathrm{d}t& =M_{12}{I}_1{\int }_0^{I_2}\mathrm{d}{i}_2+L_2{\int }_0^{I_2}{i}_2\mathrm{d}{i}_2\\ & =M_{12}{I}_1{I}_2+\frac{1}{2}{L}_2{I}_2^2\end{array}$$

把两个阶段的储存能量相加，得到总储存能量为：

$$w=w_1+w_2=\frac{1}{2}{L}_1{I}_1^2+\frac{1}{2}{L}_2{I}_2^2+M_{12}{I}_1{I}_2$$

如果反转电流达到最终值得顺序。即，先将电流 i₂ 从零增加到 I₂，然后保持为 I₂，再让电流 i₁ 从零增加到 I₁，此时总储存能量为：

$$w=\frac{1}{2}{L}_1{I}_1^2+\frac{1}{2}{L}_2{I}_2^2+M_{21}{I}_1{I}_2$$

无论到达最终值的顺序如何，总储存能量都应该是相同的。因此，可以得出结论：

$$M_{12}=M_{21}=M$$

所以

$$w=\frac{1}{2}{L}_1{I}_1^2+\frac{1}{2}{L}_2{I}_2^2+M{I}_1{I}_2$$

上述表达式是基于两个线圈的电流同时流入各自的打点端 (dotted terminal)。如果一个电流进入一个打点端，而另一个电流流出另一个打点端，那么互感电压为负，因此互感能量 M I₁ I₂ 这一项也为负。在这种情况下：

$$w=\frac{1}{2}{L}_1{I}_1^2+\frac{1}{2}{L}_2{I}_2^2-M{I}_1{I}_2$$

另外，因为 I₁ 和 I₂ 是任意的，所以电路中存储的瞬时能量具有一般表达形式：

$$\boxed{{\displaystyle w=\frac{1}{2}{L}_1{i}_1^2+\frac{1}{2}{L}_2{i}_2^2\pm M{i}_1{i}_2}}$$

如果两个电流都同时流入或同时流出打点端，则选择互感项为正；否则选择互感项为负。

因为任何被动电路在任何时刻的总储存能量 w_total 必须始终大于等于零，所以有：

$$\begin{array}{rl}\frac{1}{2}{L}_1{i}_1^2+\frac{1}{2}{L}_2{i}_2^2-M{i}_1{i}_2& \ge 0\\ (\frac{1}{2}{L}_1{i}_1^2-i_1{i}_2\sqrt{L_1{L}_2}+\frac{1}{2}{L}_2{i}_2^2)+(i_1{i}_2\sqrt{L_1{L}_2}-M{i}_1{i}_2)& \ge 0\\ \frac{1}{2}{(i_1\sqrt{L_1}-i_2\sqrt{L_2})}^2+i_1{i}_2(\sqrt{L_1{L}_2}-M)& \ge 0\\ \sqrt{L_1{L}_2}-M& \ge 0\\ M& \le \sqrt{L_1{L}_2}\end{array}$$

因此，互感系数 M 的最大值为 √(L₁ L₂)，即互感系数不能超过两个线圈自感系数乘积的平方根（即几何平均数）。互感 M 接近上限的程度通常用耦合系数 k 来衡量，其定义如下：

$$k=\frac{M}{\sqrt{L_1{L}_2}}$$

或者

$$\boxed{{\displaystyle M=k\sqrt{L_1{L}_2}}}$$

• k = 0
  • 无耦合。$L_1$ 产生的磁通量完全不穿过 $L_2$，反之亦然。它们是完全独立的电感。
• k = 1
  • 完全耦合。这是理论上的最大值。
  • $L_1$ 产生的磁通量完全穿过 $L_2$，反之亦然。没有任何磁通量泄露。
  • 这是理想变压器的假设。
• 0 < k < 1
  • 部分耦合。这是所有现实世界中的情况。
  • $L_1$ 产生的磁通量部分穿过 $L_2$ (这部分贡献了 $M$)，反之亦然。有磁通量泄露。

线性变压器

Linear Transformer

A transformer is generally a four-terminal device comprising two (or more) magnetically coupled coils.

输入阻抗和反射阻抗

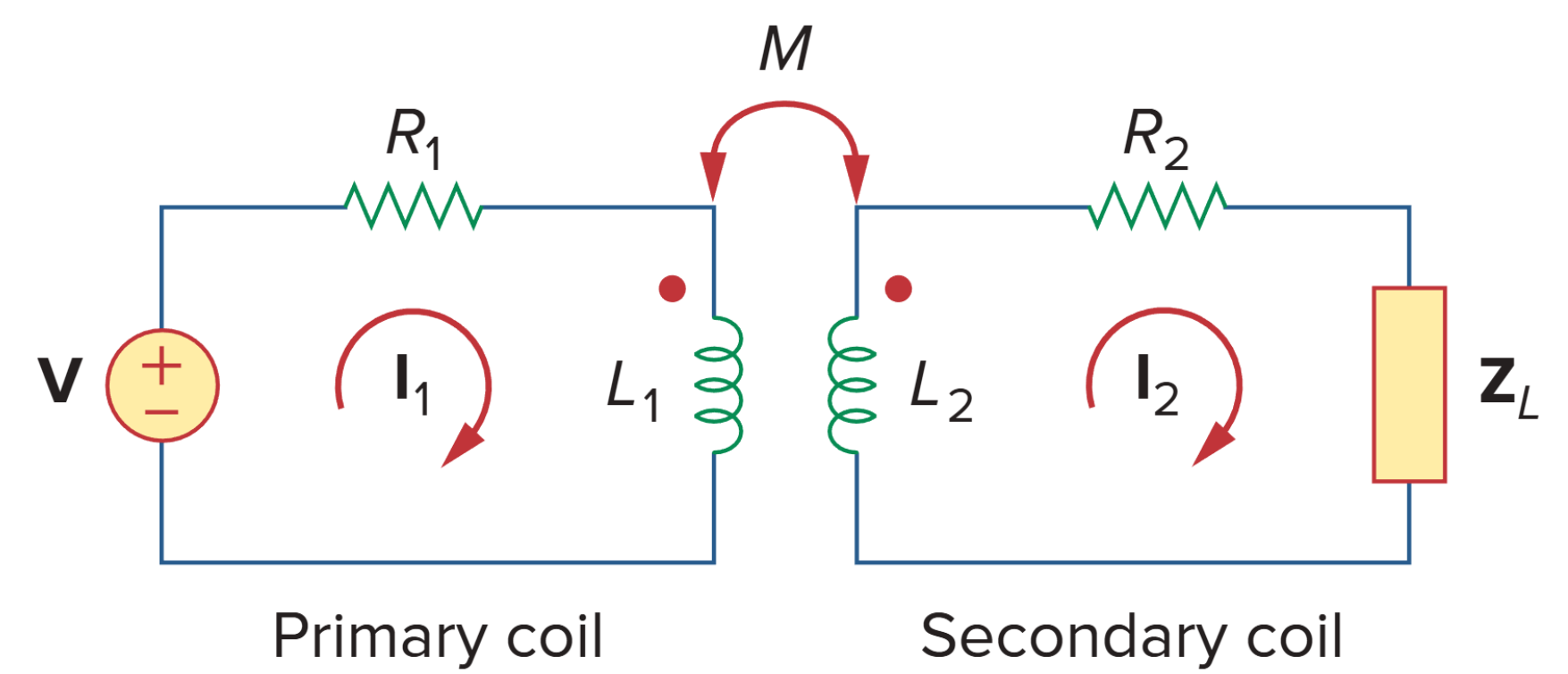
考虑求出从电源看到的输入阻抗 Z_in，因为它决定了主电路的行为。对上图所示的左右两个网孔应用 KVL 得到：

$$\begin{array}{rl}\mathbf{V}& =(R_1+j\omega L_1){\mathbf{I}}_1-j\omega M{\mathbf{I}}_2\\ 0& =-j\omega M{\mathbf{I}}_1+(R_2+j\omega L_2+{\mathbf{Z}}_L){\mathbf{I}}_2\end{array}$$

最终可以得到：

$${\mathbf{Z}}_{\mathrm{in}}=\frac{\mathbf{V}}{{\mathbf{I}}_1}=R_1+j\omega L_1+\frac{{\omega }^2{M}^2}{R_2+j\omega L_2+{\mathbf{Z}}_L}$$

其中，第三项

$$\boxed{{\displaystyle {\mathbf{Z}}_R=\frac{{\omega }^2{M}^2}{R_2+j\omega L_2+{\mathbf{Z}}_L}}}$$

被称作反射阻抗 (reflected impedance)。其是由主绕组和副绕组之间的互感引起的。

注意，反射阻抗的结果不受变压器上打点位置的影响，因为当 M 被替换为 -M 时，会产生相同的结果。

原始电路

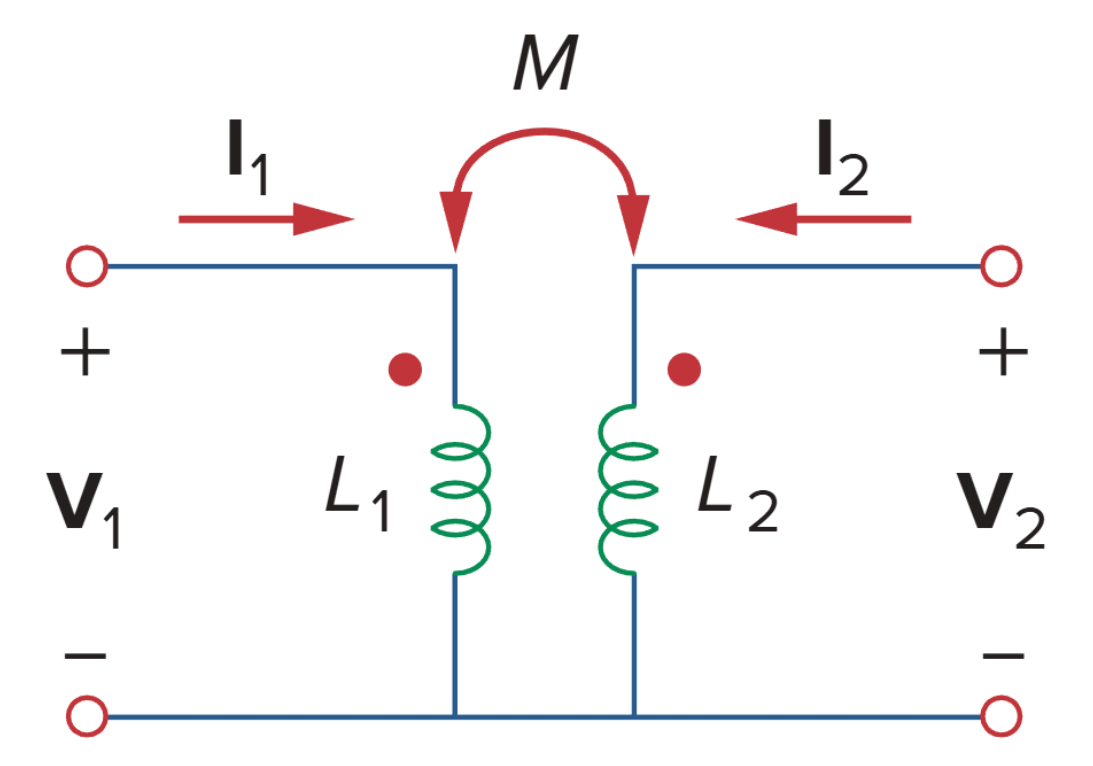
如上图所示，对左右两个网孔应用 KVL 得到：

$$\left[\begin{array}{c}{\mathbf{V}}_1\\ {\mathbf{V}}_2\end{array}\right]=\left[\begin{array}{cc}j\omega L_1& j\omega M\\ j\omega M& j\omega L_2\end{array}\right]\left[\begin{array}{c}{\mathbf{I}}_1\\ {\mathbf{I}}_2\end{array}\right]$$

对矩阵进行求逆，得到：

$$\left[\begin{array}{c}{\mathbf{I}}_1\\ {\mathbf{I}}_2\end{array}\right]=\left[\begin{array}{cc}{\displaystyle \frac{L_2}{j\omega (L_1{L}_2-M^2)}}& {\displaystyle \frac{-M}{j\omega (L_1{L}_2-M^2)}}\\ {\displaystyle \frac{-M}{j\omega (L_1{L}_2-M^2)}}& {\displaystyle \frac{L_1}{j\omega (L_1{L}_2-M^2)}}\end{array}\right]\left[\begin{array}{c}{\mathbf{V}}_1\\ {\mathbf{V}}_2\end{array}\right]$$

使用 mathematica 求逆矩阵：

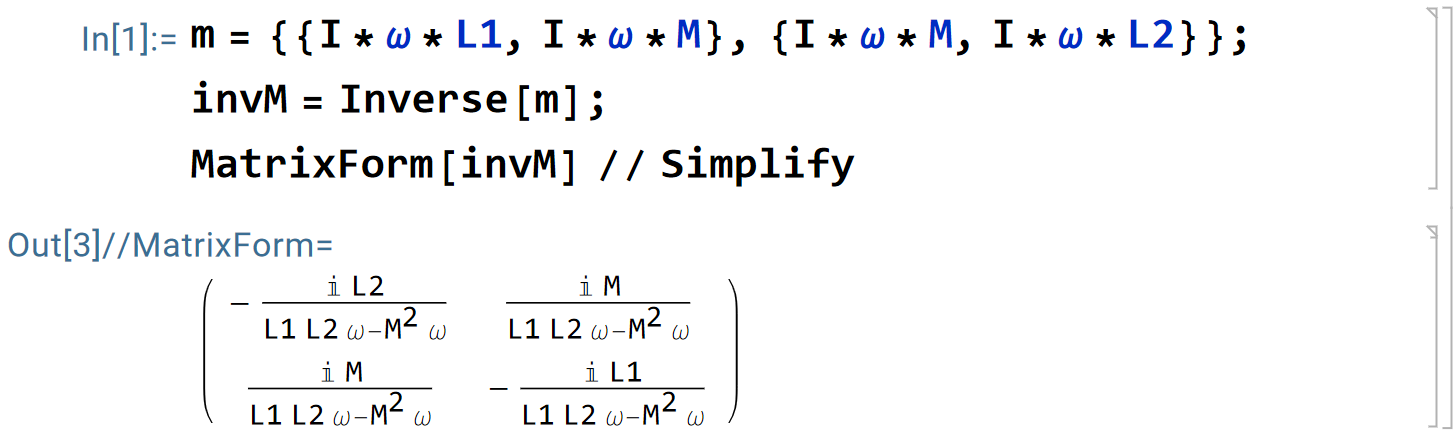
接下来的内容中，在推导磁耦合电路的等效电路时，将采用待定系数法进行分析。

等效 T 电路

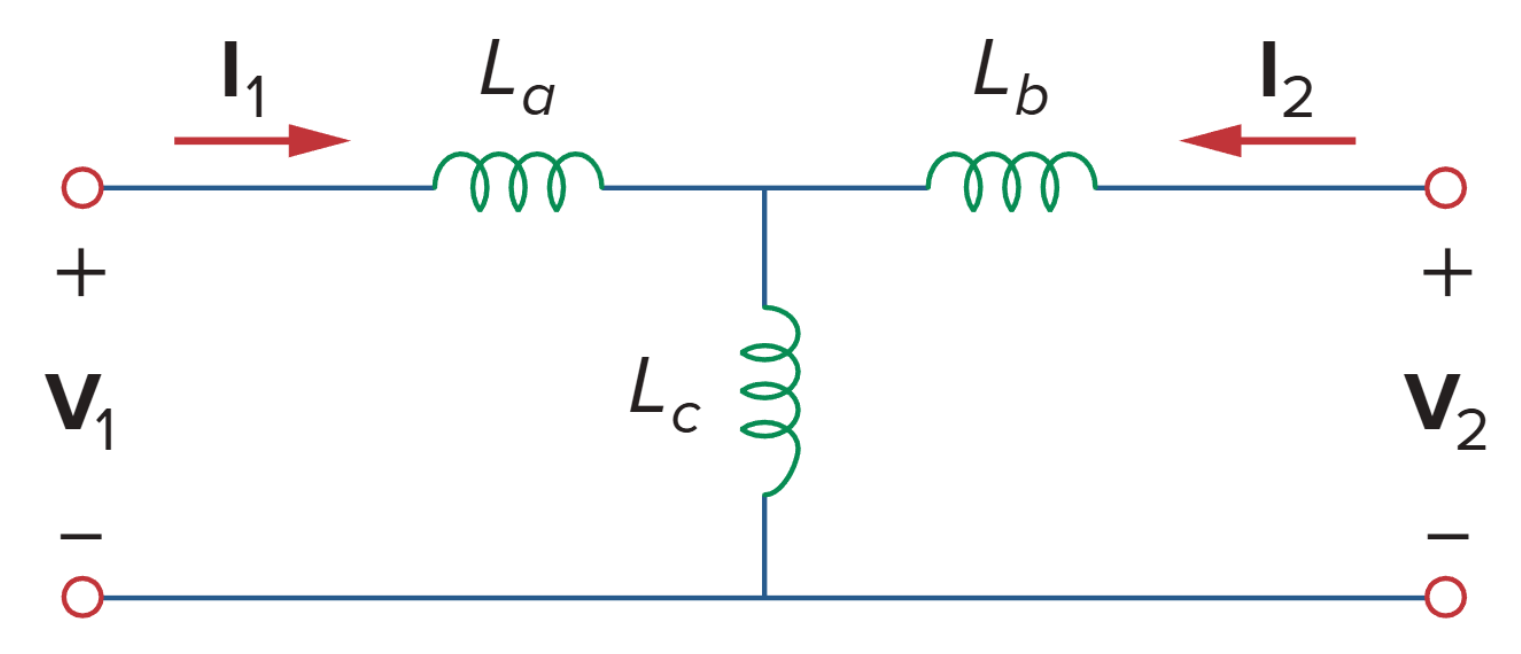
对等效 T 电路应用 KVL 得到：

$$\left[\begin{array}{c}{\mathbf{V}}_1\\ {\mathbf{V}}_2\end{array}\right]=\left[\begin{array}{cc}j\omega (L_a+L_c)& j\omega L_c\\ j\omega L_c& j\omega (L_b+L_c)\end{array}\right]\left[\begin{array}{c}{\mathbf{I}}_1\\ {\mathbf{I}}_2\end{array}\right]$$

利用待定系数法，可以得到：

$$\boxed{{\displaystyle L_a=L_1-M,L_b=L_2-M,L_c=M}}$$

等效 Π 电路

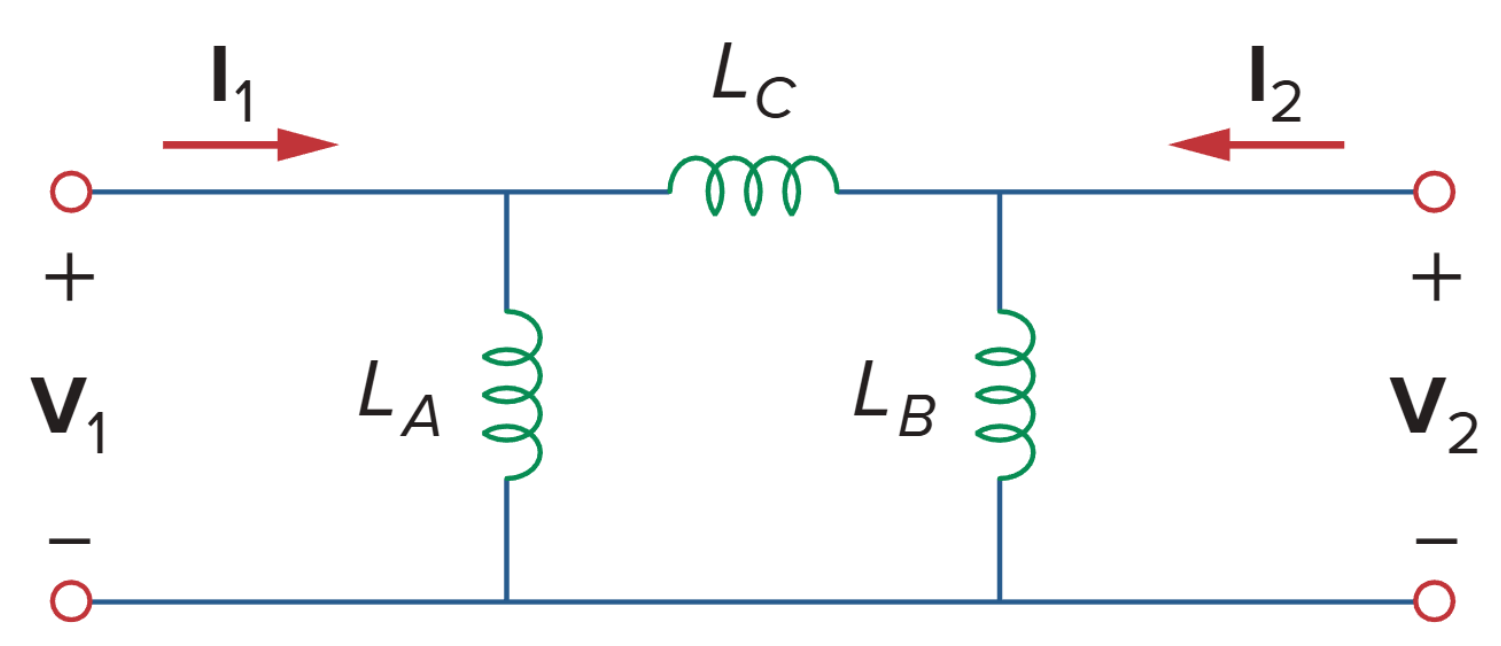
对等效 Π 电路应用 KCL 得到：

$$\left[\begin{array}{c}{\mathbf{I}}_1\\ {\mathbf{I}}_2\end{array}\right]=\left[\begin{array}{cc}{\displaystyle \frac{1}{j\omega L_A}+{\displaystyle \frac{1}{j\omega L_C}}}& -{\displaystyle \frac{1}{j\omega L_C}}\\ -{\displaystyle \frac{1}{j\omega L_C}}& {\displaystyle \frac{1}{j\omega L_B}+{\displaystyle \frac{1}{j\omega L_C}}}\end{array}\right]\left[\begin{array}{c}{\mathbf{V}}_1\\ {\mathbf{V}}_2\end{array}\right]$$

利用待定系数法，可以得到：

$$\boxed{{\displaystyle L_A={\displaystyle \frac{L_1{L}_2-M^2}{L_2-M},L_B={\displaystyle \frac{L_1{L}_2-M^2}{L_1-M},L_C={\displaystyle \frac{L_1{L}_2-M^2}{M}}}}}}$$

注：在上述两种等效电路中，各电感器之间不存在互感作用。需要注意的是，互感系数 M 取负值在物理上并无实际意义，但从数学角度来看，等效模型依然成立。

理想变压器

Ideal Transformers

模型假设

1. 绕组电阻为零 (R₁ = 0 = R₂)
   • 内容：无论是初级绕组（接电源一侧）还是次级绕组（接负载一侧），制造它们的导线（通常是铜线）完全没有电阻。
   • 这说明了：电流流过这些“完美”导线时，不会产生 I²R 的热量耗损（即焦耳热），也不会在绕组自身上产生任何电压降。能量在导线中没有损失。
2. 铁芯磁导率无限大 (μ -> ∞)
   • 内容：用来传导磁通量的铁芯（或磁芯），其“导磁”能力无限强。
   • 这说明了：只需要无穷小的激励电流，就可以在铁芯中建立起工作所需的磁通量。
   • 重要推论：在分析中，我们可以忽略这个激励电流。这意味着所有输入的电流都 100% 参与了能量的传递，而不是“浪费”在建立磁场上。
3. 无磁漏 (Zero Leakage Flux)
   • 内容：这是一个完美耦合的假设。初级绕组产生的所有磁通量，都 100% 地穿过铁芯，并 100% 地被次级绕组“接收”（专业术语叫做“匝链”），反之亦然。没有任何磁通量“泄露”到空气中。
   • 这说明了：能量通过磁场传递的效率是 100% 的。
   • 重要推论：既然磁通量是完美传递的，那么初级和次级绕组的感应电压之比，就严格等于它们的匝数（线圈圈数）之比。
4. 铁芯损耗为零 (Zero Core Losses)
   • 内容：在实际的交流磁场中，铁芯会因为磁场不断变化而发热。这种损耗主要分为两种：
     1. 磁滞损耗 (Hysteresis Loss)：磁性材料在磁化过程中，由于磁畴的旋转和摩擦，会产生能量损耗。
     2. 涡流损耗 (Eddy Current Loss)：在变化的磁场中，铁芯内部会产生感应电流，这些电流在铁芯内形成闭合回路，产生电阻损耗。
   • 这说明了：理想变压器假设这两种损耗完全不存在。铁芯在工作时是“冷静”的，不发热，不消耗能量。

教材推导

如上图。应用 KVL 得到：

$$\begin{array}{rl}{\mathbf{V}}_1& =j\omega L_1{\mathbf{I}}_1+j\omega M{\mathbf{I}}_2\\ {\mathbf{V}}_2& =j\omega M{\mathbf{I}}_1+j\omega L_2{\mathbf{I}}_2\end{array}$$

将 ${\mathbf{I}}_{\mathbf{1}}={\displaystyle \frac{{\mathbf{V}}_1-j\omega M{\mathbf{I}}_2}{j\omega L_1}}$ 代入上式，得到：

$${\mathbf{V}}_2=j\omega L_2{\mathbf{I}}_2+\frac{M{\mathbf{V}}_1}{L_1}-\frac{j\omega M^2{\mathbf{I}}_2}{L_1}$$

理想变压器满足 $M=1\cdot \sqrt{L_1{L}_2}$，所以有：

$${\mathbf{V}}_2=j\omega L_2{\mathbf{I}}_2+\frac{\sqrt{L_1{L}_2}{\mathbf{V}}_1}{L_1}-\frac{j\omega L_1{L}_2{\mathbf{I}}_2}{L_1}=\sqrt{\frac{L_2}{L_1}}{\mathbf{V}}_1=n{\mathbf{V}}_1$$

其中，$n=\sqrt{{\displaystyle \frac{L_2}{L_1}}}$ 被称为匝数比 (turns ratio)。

1. Coils have very large reactances (L₁, L₂, M → ∞).
2. Coupling coefficient is equal to unity (k = 1).
3. Primary and secondary coils are lossless (R₁ = 0 = R₂).

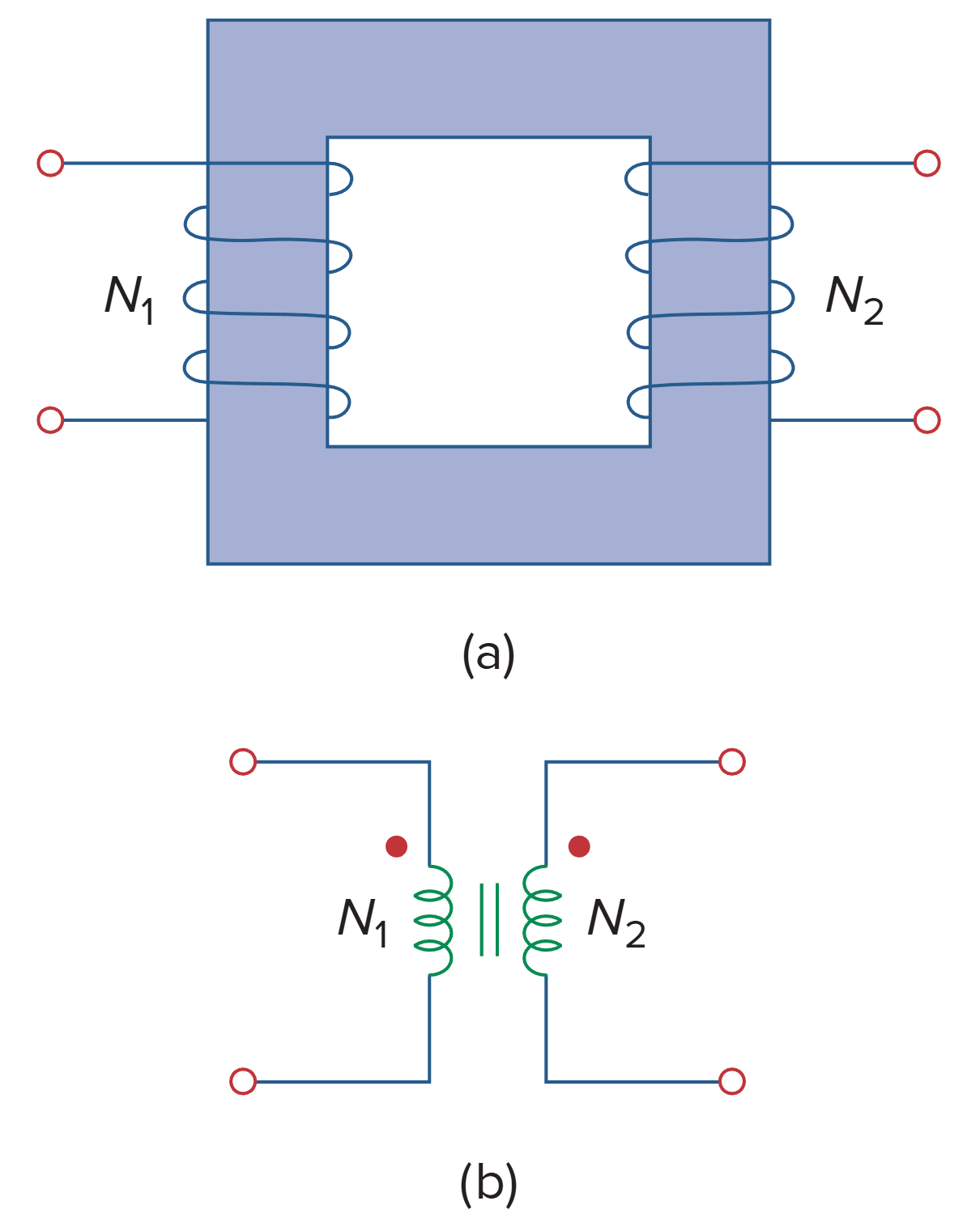
根据法拉第定律，初级绕组的电压为：

$$v_1=N_1\frac{\mathrm{d}\varphi }{\mathrm{d}t}$$

根据理想变压器的假设，次级绕组的电压为：

$$v_2=N_2\frac{\mathrm{d}\varphi }{\mathrm{d}t}$$

因此，初级和次级绕组的电压之比为：

$$\frac{v_1}{v_2}=\frac{N_1}{N_2}=n$$

其中，n 为匝数比 (turns ratio) 或变压比 (transformer ratio)。我们可以用相域模型来表示理想变压器：

$$\boxed{{\displaystyle \frac{{\mathbf{V}}_2}{{\mathbf{V}}_1}=\frac{N_2}{N_1}=n}}$$

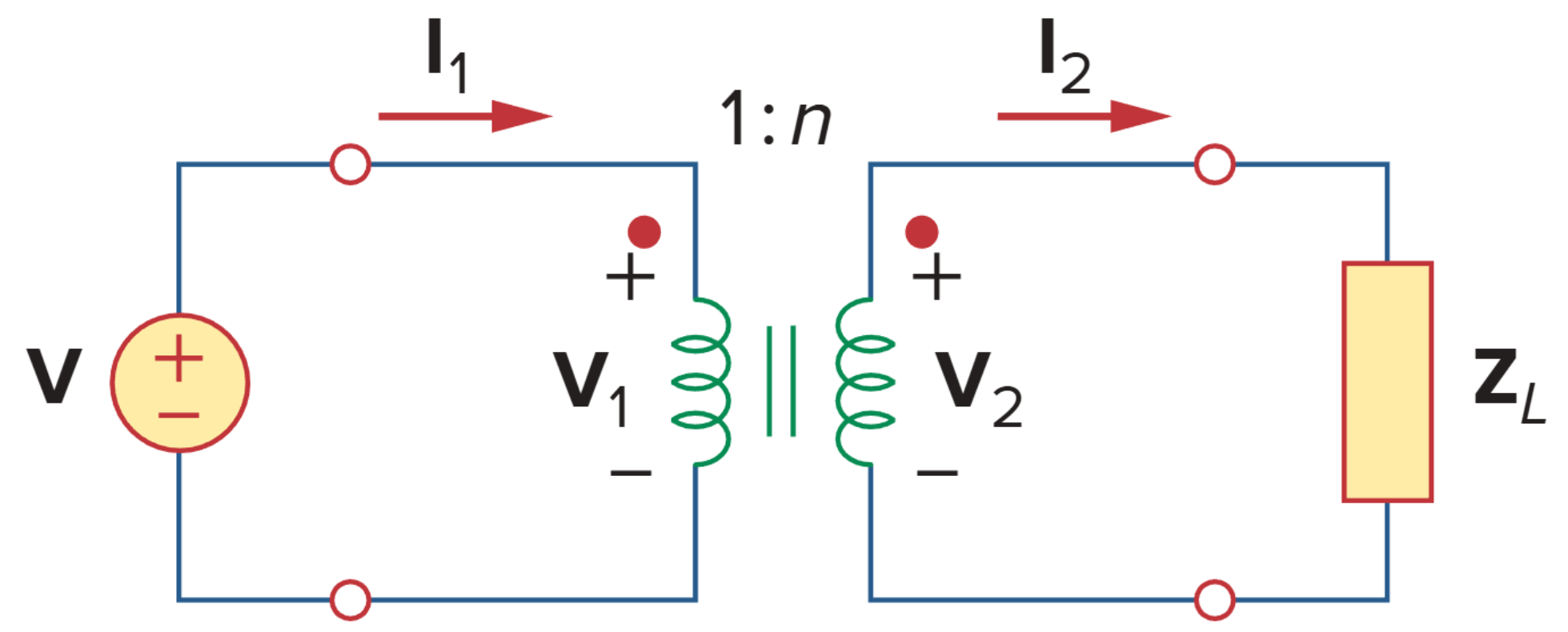
由于能量守恒定律，初级绕组释放的能量必须等于次级绕组吸收的能量，又由于理想变压器中没有损耗。这意味着：

$$v_1{i}_1=v_2{i}_2$$

用相域表达为：

$$\frac{{\mathbf{V}}_2}{{\mathbf{V}}_1}=\frac{{\mathbf{I}}_1}{{\mathbf{I}}_2}=n$$

因此：

$$\boxed{{\displaystyle \frac{{\mathbf{I}}_2}{{\mathbf{I}}_1}=\frac{N_1}{N_2}=\frac{1}{n}}}$$

• n = 1: Isolation Transformer
• n > 1: Step-up Transformer
• n < 1: Step-down Transformer

复功率为：

$${\mathbf{S}}_1={\mathbf{V}}_1{\mathbf{I}}_1^{\ast }={\mathbf{V}}_2{\mathbf{I}}_2^{\ast }={\mathbf{S}}_2$$

考虑阻抗：

$${\mathbf{Z}}_{\text{in}}=\frac{{\mathbf{V}}_1}{{\mathbf{I}}_1}=\frac{1}{n^2}\frac{{\mathbf{V}}_2}{{\mathbf{I}}_2}=\frac{{\mathbf{Z}}_L}{n^2}$$

输入阻抗也被称为反射阻抗，因为他看起来就像是负载阻抗被反射到初级绕组侧。

理想自耦变压器

Ideal Autotransformer

An autotransformer is a transformer in which both the primary and the secondary are in a single winding.

Step-down autotransformer

$$\boxed{{\displaystyle \frac{{\mathbf{V}}_1}{{\mathbf{V}}_2}=\frac{N_1+N_2}{N_2}}}$$

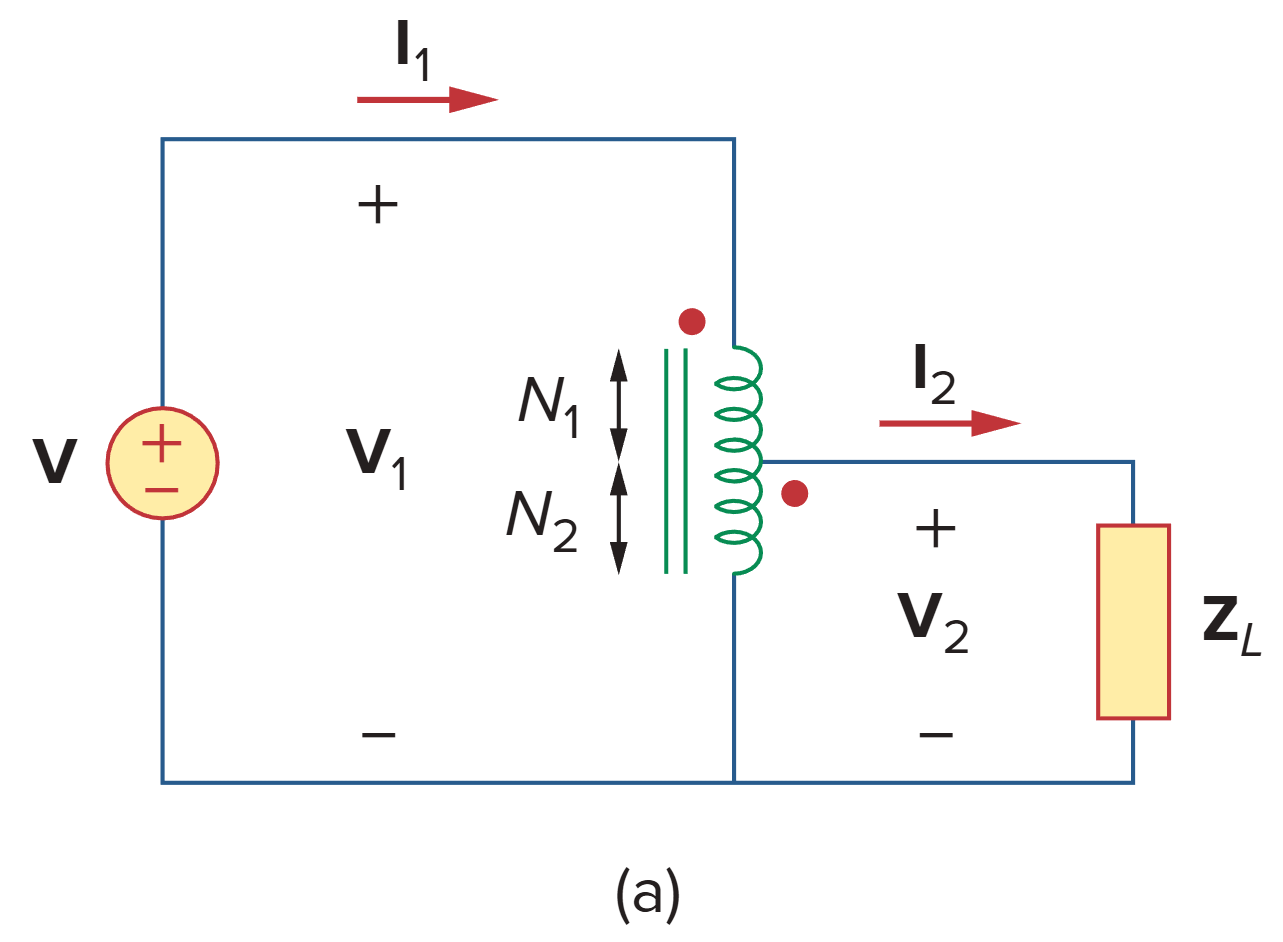
Step-up autotransformer

$$\boxed{{\displaystyle \frac{{\mathbf{V}}_1}{{\mathbf{V}}_2}=\frac{N_1}{N_1+N_2}}}$$

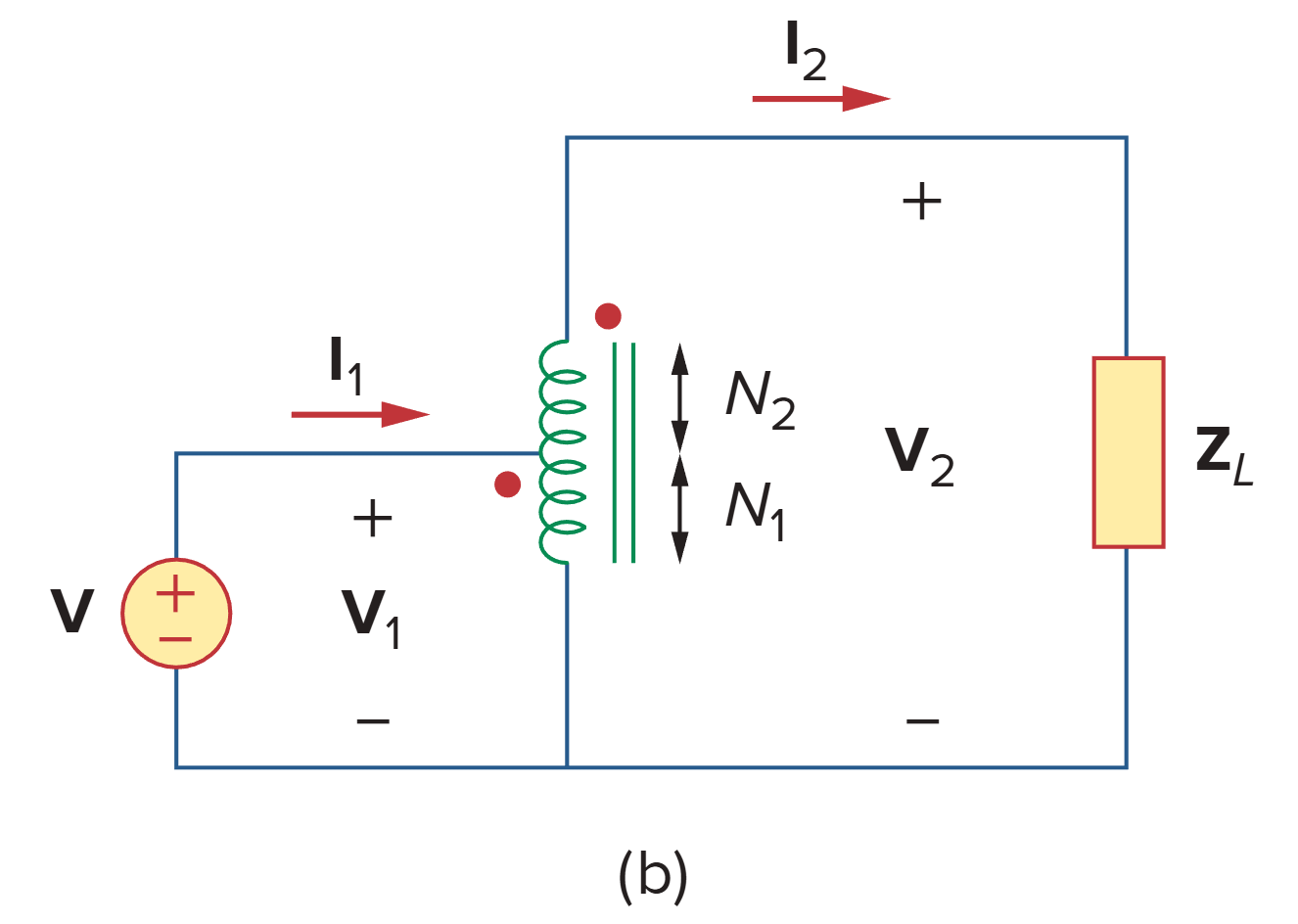
理想自耦变压器是一种“省料版”的理想变压器，它通过“共用绕组”的方式，牺牲了电器隔离安全性，换来了在特定场合下极高的效率、极低的成本和更小的体积。

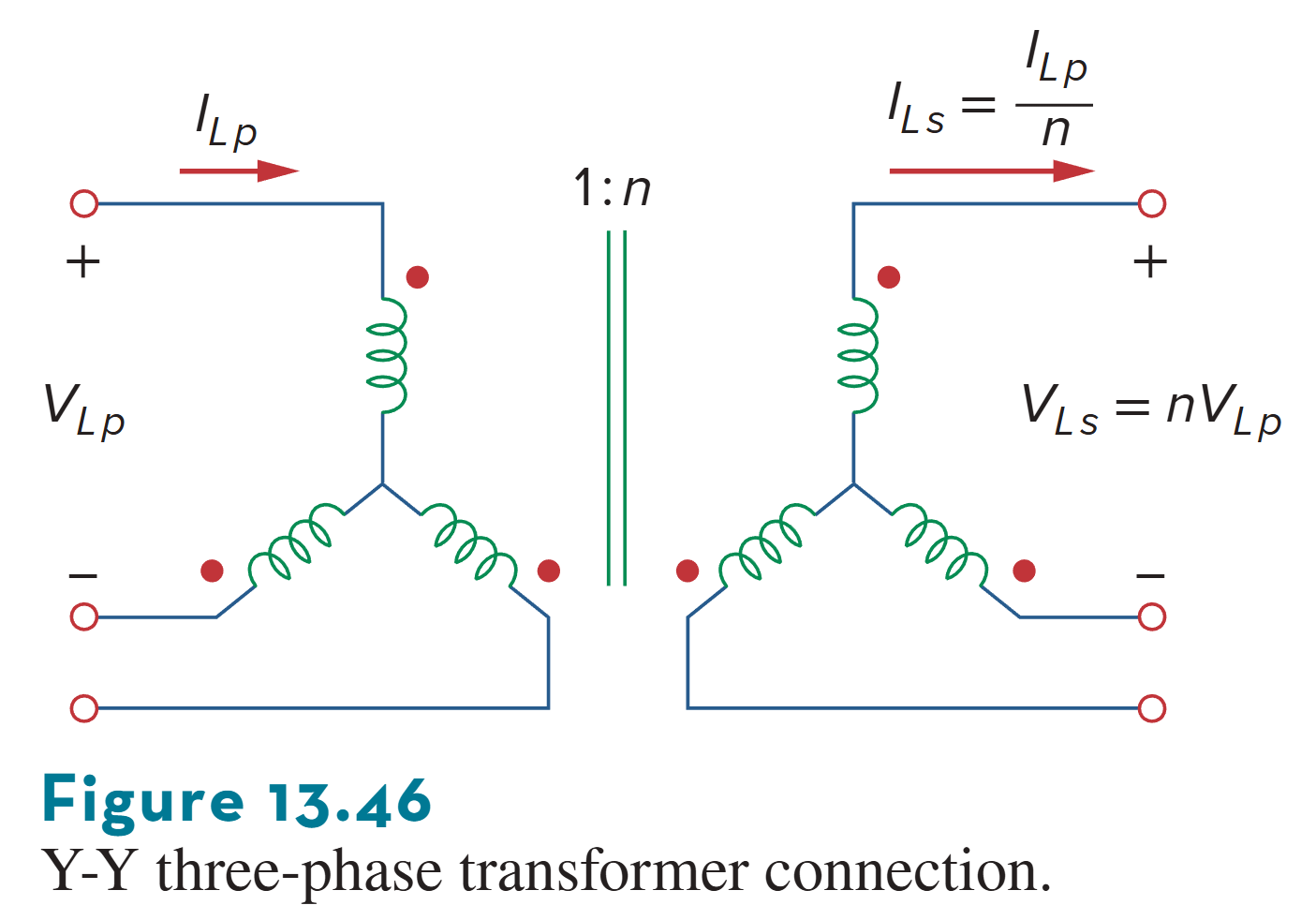
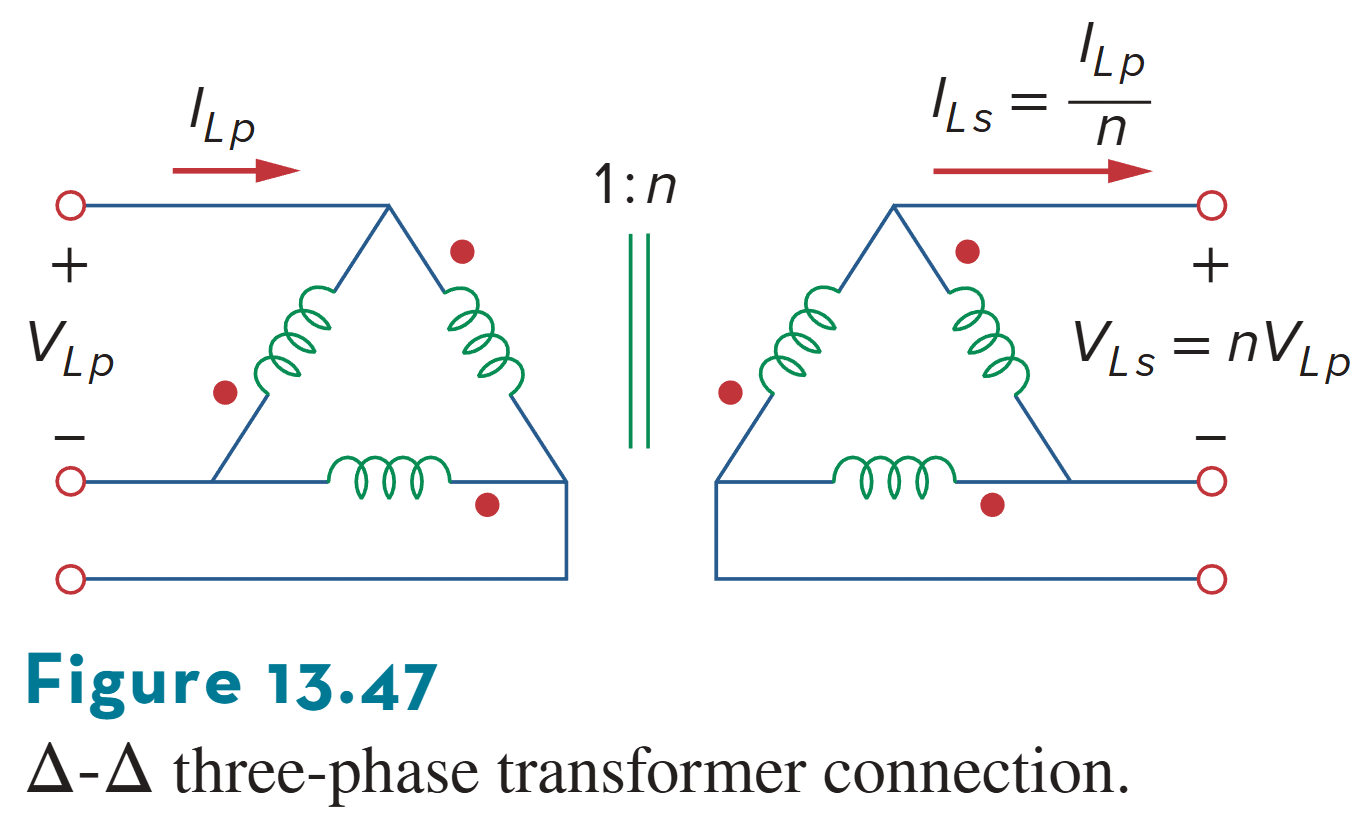
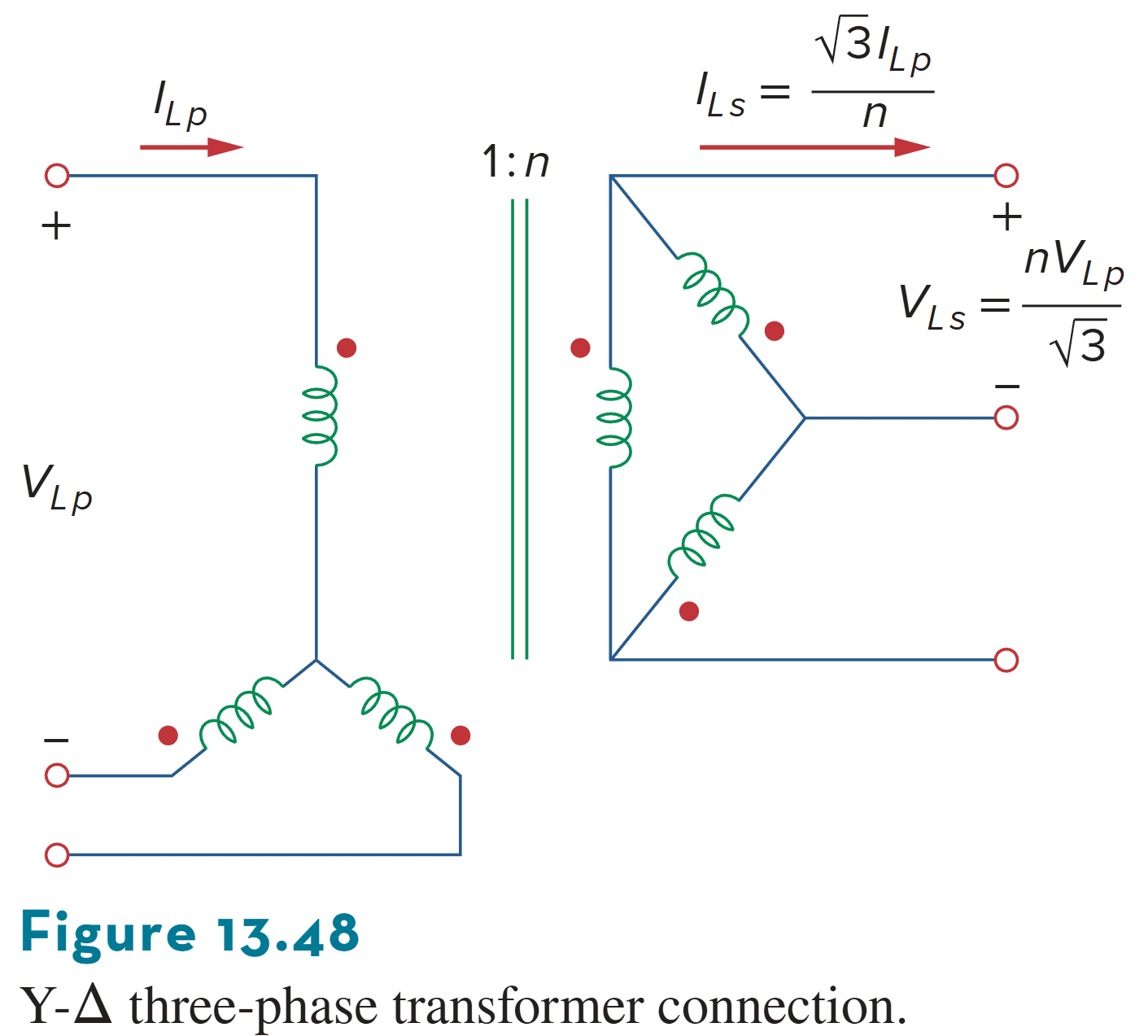
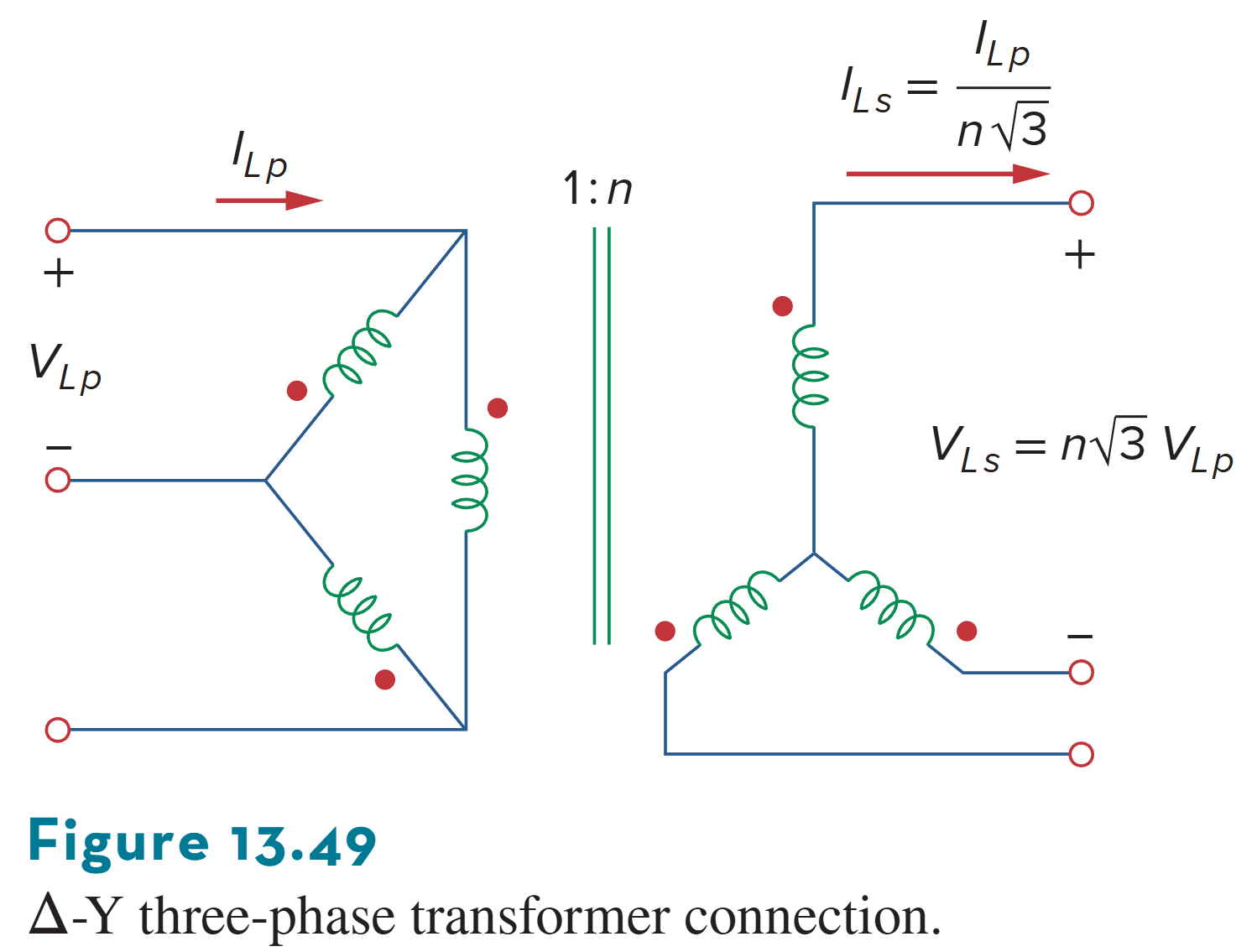
*三相变压器

Three-Phase Transformer