频率响应

Frequency Response

传递函数

Transfer Function

The transfer function $\mathbf{H}(\omega )$ of a circuit is the frequency-dependent ratio of a phasor output $\mathbf{Y}(\omega )$ (an element voltage or current) to a phasor input $\mathbf{X}(\omega )$ (source voltage or current).

$$\mathbf{H}(\omega )=\frac{\mathbf{Y}(\omega )}{\mathbf{X}(\omega )}$$

The transfer function $\mathbf{H}(\omega )$ can be expressed in terms of its numerator polynomial $\mathbf{N}(\omega )$ and denominator polynomial $\mathbf{D}(\omega )$ as

$$\mathbf{H}(\omega )=\frac{\mathbf{N}(\omega )}{\mathbf{D}(\omega )}$$

The roots of $\mathbf{N}(\omega )=0$ are called the zeros and usually represented by $j\omega =z_1,z_2,\dots$

Similarly, the roots of $\mathbf{D}(\omega )=0$ are called the poles and usually represented by $j\omega =p_1,p_2,\dots$

为了避免复数运算，有时会使用 $s$ 代替 $j\omega$。

分贝刻度

The Decibel Scale

在通信领域，增益 (gain) 使用贝尔 (bels) 衡量。历史上，贝尔用于衡量两个功率等级的比率，或者说是功率增益 G:

$$G=\text{Number of bels}={\log }_{10}\frac{P_2}{P_1}$$

分贝 (decibels) 提供了一个量级更小的单位。1 分贝等于 1 贝尔的十分之一。其定义由下列公式给出：

$$\boxed{{\displaystyle G_{\text{dB}}=10{\log }_{10}\frac{P_2}{P_1}}}$$

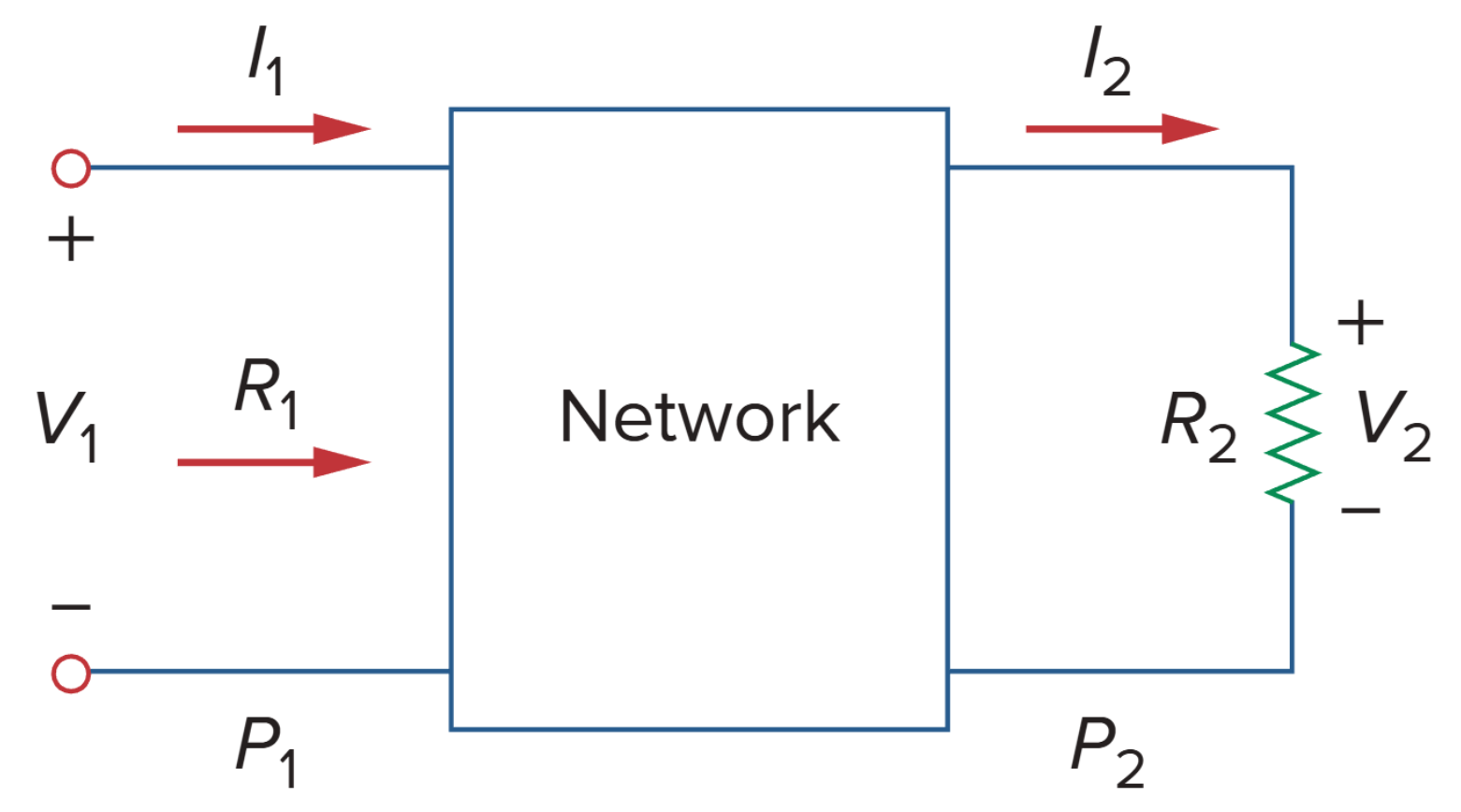
考虑如图所示的电路，分析其功率之比：

$$\begin{array}{rl}{G}_{\text{dB}}& =10{\log }_{10}\frac{P_2}{P_1}\\ & =10{\log }_{10}\frac{V_2^2/R_2}{V_1^2/R_1}\\ & =10{\log }_{10}{\left(\frac{V_2}{V_1}\right)}^2-10{\log }_{10}\frac{R_2}{R_1}\end{array}$$

在 $R_1=R_2$ 的情况下（这是一个在比较电压时，经常被假设的条件），上述公式变为：

$$\boxed{{\displaystyle G_{\text{dB}}=20{\log }_{10}\frac{V_2}{V_1}}}$$

同理也有：

$$G_{\text{dB}}=20{\log }_{10}\frac{I_2}{I_1}$$

波特图

Bode Plots

传递函数的极坐标形式：

$$\mathbf{H}=H\mathrm{\angle }\varphi =H{e}^{j\varphi }$$

对上述等式的两边求对数：

$$\ln \mathbf{H}=\ln H+\ln e^{j\varphi }=\ln H+j\varphi$$

在波特图中，横轴为 $\omega$，纵轴为 $H_{\text{dB}}$ 和 $\varphi$。

$$\boxed{{\displaystyle \phantom{{\displaystyle \frac{1}{1}}}{H}_{\text{dB}}=20{\log }_{10}H\phantom{{\displaystyle \frac{1}{1}}}}}$$

$\mathbf{H}(\omega )$ 的标准形式 (standard form) 为：

$$H(\omega )=\frac{K(j\omega {)}^{\pm 1}(1+j\omega /z_1)[1+j2{\zeta }_1\omega /{\omega }_k+(j\omega /{\omega }_k{)}^2]\cdots }{(1+j\omega /p_1)[1+j2{\zeta }_2\omega /{\omega }_n+(j\omega /{\omega }_n{)}^2]\cdots }$$

其中的“七种因式”：

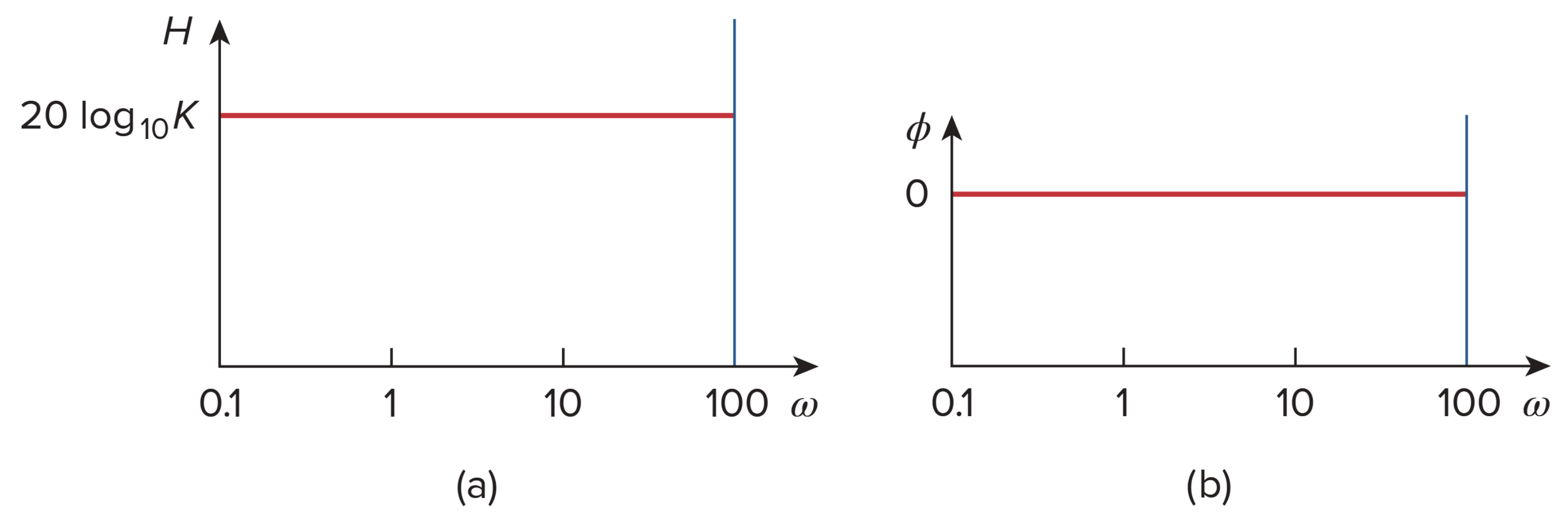
1. 增益 K，一条水平直线
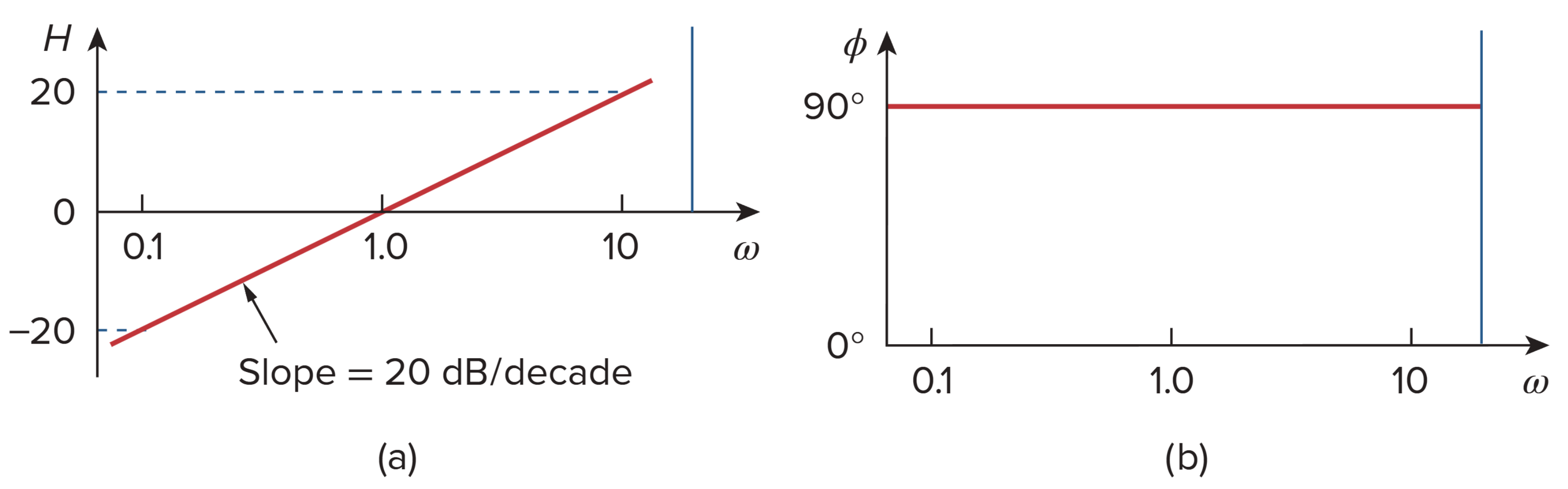
2. 原点零点 (a zero at the origin) $(j\omega )$
3. 原点极点 (a pole at the origin) $(j\omega {)}^{-1}$
4. 简单零点 (a simple zero) $(1+j\omega /z_1)$
5. 简单极点 (a simple pole) $1/(1+j\omega /p_1)$
6. 二次零点 (a quadratic zero) $[1+j2{\zeta }_1\omega /{\omega }_k+(j\omega /{\omega }_k{)}^2]$
7. 二次极点 (a quadratic pole) $1/[1+j2{\zeta }_2\omega /{\omega }_n+(j\omega /{\omega }_n{)}^2]$

Constant term

$$\begin{array}{rl}{H}_{\text{dB}}& =20{\log }_{10}\left|K\right|\\ \varphi & =\{\begin{array}{ll}0\mathrm{°},& K>0\\ \pm 180\mathrm{°},& K<0\end{array}\end{array}$$

Pole/zero at the origin

$$\begin{array}{rl}{H}_{\text{dB}}& =20{\log }_{10}|(j\omega {)}^N|\\ & =20N{\log }_{10}\omega \\ \varphi & =90\mathrm{°}N\end{array}$$

其中，$N\in \mathbb{Z}$。

Simple pole/zero

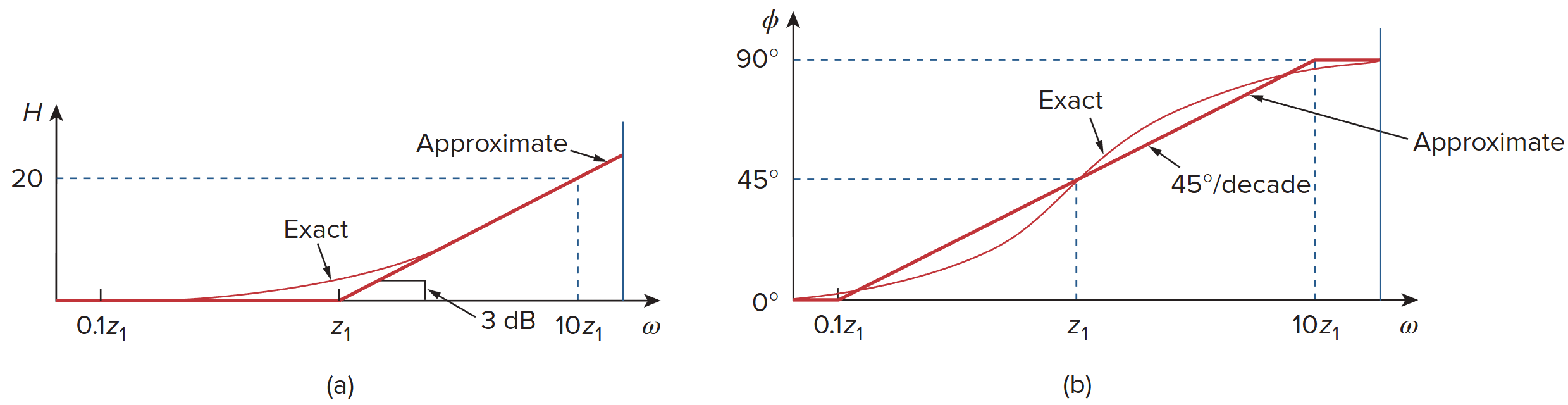
核心公式

$$H(\omega )={(1+\frac{j\omega }{r_1})}^N$$

其中 $N$ 是整数。$r_1$ 在 $N>0$ 时代表零点 $z_1$，在 $N<0$ 时代表极点 $p_1$。

幅值

$$\begin{array}{rl}{H}_{\text{dB}}& =20{\log }_{10}\left|{(1+\frac{j\omega }{r_1})}^N\right|\\ & =20N{\log }_{10}|1+\frac{j\omega }{r_1}|\\ H_{\text{dB}}& \approx 20N{\log }_{10}1=0,& \text{when }\omega \ll r_1\\ H_{\text{dB}}& \approx 20N{\log }_{10}\frac{\omega }{r_1},& \text{when }\omega \gg r_1\end{array}$$

对于幅值，只有一个转折点 $\omega =r_1$：

• 当 $\omega <r_1$ 时，斜率为 0 dB/decade； $H_{\text{dB}}=0\text{ dB}$；
• 当 $\omega =r_1$ 时，斜率从 0 变为 20 N dB/decade；
• 当 $\omega >r_1$ 时，斜率为 20 N dB/decade；

相位

$$\varphi =N\cdot {\tan }^{-1}\frac{\omega }{r_1}=\{\begin{array}{l}0,\omega =0\\ 45\mathrm{°}N,\omega =r_1\\ 90\mathrm{°}N,\omega \to \mathrm{\infty }\end{array}$$

对于相位，有两个转折点 $\omega =0.1r_1$ 和 $\omega =10r_1$：

• 当 $\omega <0.1r_1$ 时，$\varphi =0\mathrm{°}$；
• 当 $\omega =0.1r_1$ 时，斜率从 0° 变为 45° N/decade；
• 当 $\omega =r_1$ 时，$\varphi =45\mathrm{°}N$；
• 当 $\omega =10r_1$ 时，斜率从 45° N 变为 0° N/decade；
• 当 $\omega >10r_1$ 时，$\varphi =90\mathrm{°}N$；

Quadratic pole/zero

核心公式

$$H(\omega )={[1+\frac{j2{\zeta }_2\omega }{{\omega }_n}+{\left(\frac{j\omega }{{\omega }_n}\right)}^2]}^N$$

其中 $N$ 为整数，其中 $N>0$ 表示零点，$N<0$ 表示极点。${\omega }_n$ 为自然频率，${\zeta }_2$ 为阻尼比。

幅值

$$\begin{array}{rl}{H}_{\text{dB}}& =20{\log }_{10}\left|{[1+\frac{j2{\zeta }_2\omega }{{\omega }_n}+{\left(\frac{j\omega }{{\omega }_n}\right)}^2]}^N\right|\\ & =20N{\log }_{10}|1+\frac{j2{\zeta }_2\omega }{{\omega }_n}+{\left(\frac{j\omega }{{\omega }_n}\right)}^2|\\ H_{\text{dB}}& \approx 20N{\log }_{10}1=0,& \text{when }\omega \ll {\omega }_n\\ H_{\text{dB}}& \approx 20N{\log }_{10}\frac{{\omega }^2}{{\omega }_n^2}=40N{\log }_{10}\frac{\omega }{{\omega }_n},& \text{when }\omega \gg {\omega }_n\end{array}$$

对于幅值，只有一个转折点 $\omega ={\omega }_n$：

• 当 $\omega <{\omega }_n$ 时，斜率为 0 dB/decade； $H_{\text{dB}}=0\text{ dB}$；
• 当 $\omega ={\omega }_n$ 时，斜率从 0 变为 40 N dB/decade；
• 当 $\omega >{\omega }_n$ 时，斜率为 40 N dB/decade；

相位

$$\varphi =N\cdot {\tan }^{-1}\frac{2{\zeta }_2\omega /{\omega }_n}{1-{\omega }^2/{\omega }_n^2}=\{\begin{array}{l}0,\omega =0\\ 90\mathrm{°}N,\omega ={\omega }_n\\ 180\mathrm{°}N,\omega \to \mathrm{\infty }\end{array}$$

对于相位，有两个转折点 $\omega =0.1{\omega }_n$ 和 $\omega =10{\omega }_n$：

• 当 $\omega <0.1{\omega }_n$ 时，$\varphi =0\mathrm{°}$；
• 当 $\omega =0.1{\omega }_n$ 时，斜率从 0° 变为 90° N/decade；
• 当 $\omega ={\omega }_n$ 时，$\varphi =90\mathrm{°}N$；
• 当 $\omega =10{\omega }_n$ 时，斜率从 90° N/decade 变为 0° N/decade；
• 当 $\omega >10{\omega }_n$ 时，$\varphi =180\mathrm{°}N$；

Summary

谐振

串联谐振

Series Resonance

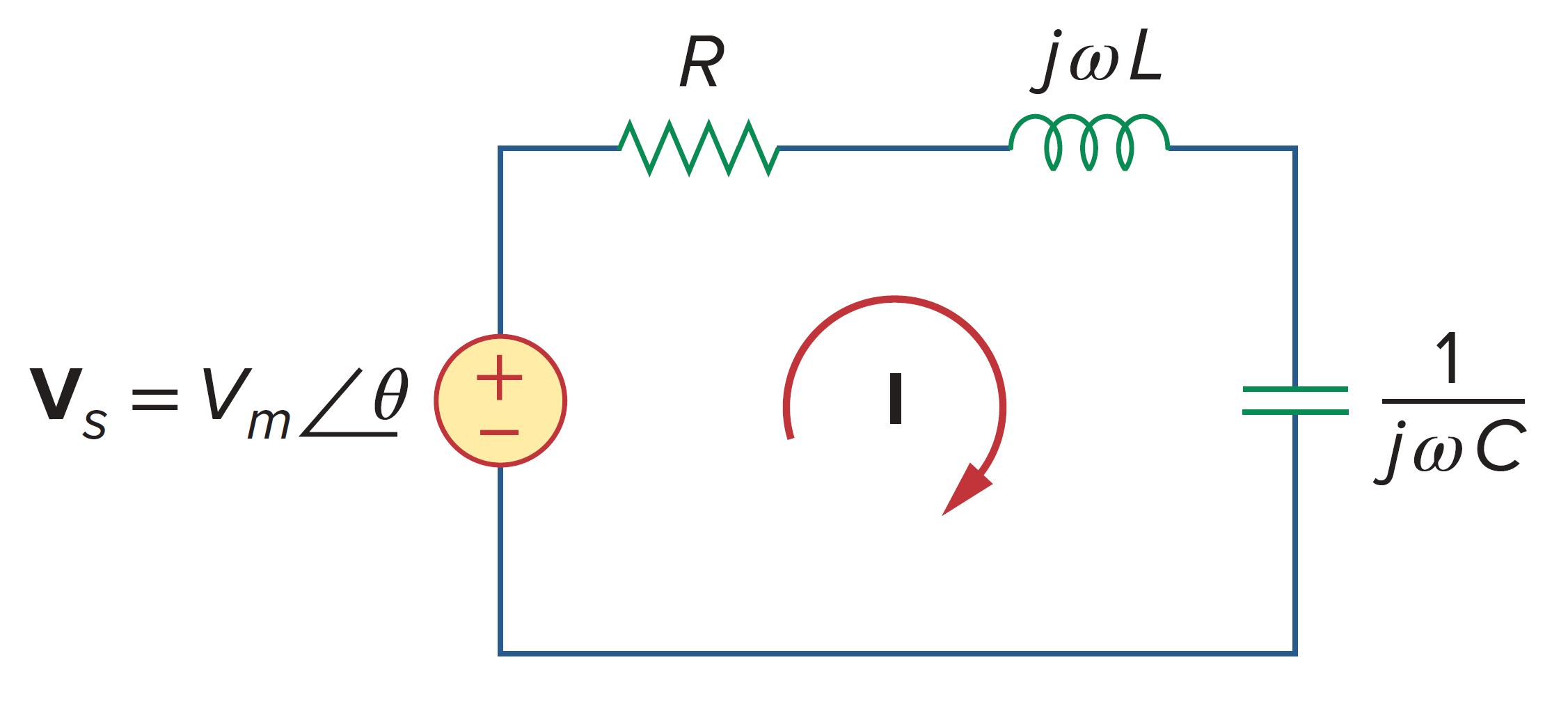
如图。

输入阻抗为

$$\mathbf{Z}=\mathbf{H}(\omega )=\frac{{\mathbf{V}}_s}{\mathbf{I}}=R+j\omega L+\frac{1}{j\omega C}$$

或

$$\mathbf{Z}=R+j(\omega L-\frac{1}{\omega C})$$

当传递函数的虚部为零时，即产生谐振

$$\text{Im}(\mathbf{Z})=\omega L-\frac{1}{\omega C}=0$$

满足此条件的 $\omega$ 称为谐振频率 ${\omega }_0$。因此

$${\omega }_{0}L=\frac{1}{{\omega }_{0}C}$$

或

$$\boxed{{\displaystyle {\omega }_0=\frac{1}{\sqrt{LC}}\text{rad/s}}}$$

由于 ${\omega }_0=2\pi f_0$，所以

$$f_0=\frac{1}{2\pi \sqrt{LC}}\text{Hz}$$

注意，谐振电路意味着

1. 阻抗时纯电阻，因此 Z = R。换句话说，LC 串联组合的作用相当于短路，全部电压都施加在 R 上。
2. 电压 V_s 和电流 I 同相，因此功率系数为 1。
3. 传递函数 H(ω) = Z(ω) 的幅值达到最小值。
4. 电感电压和电容电压可能远远大于源电压。

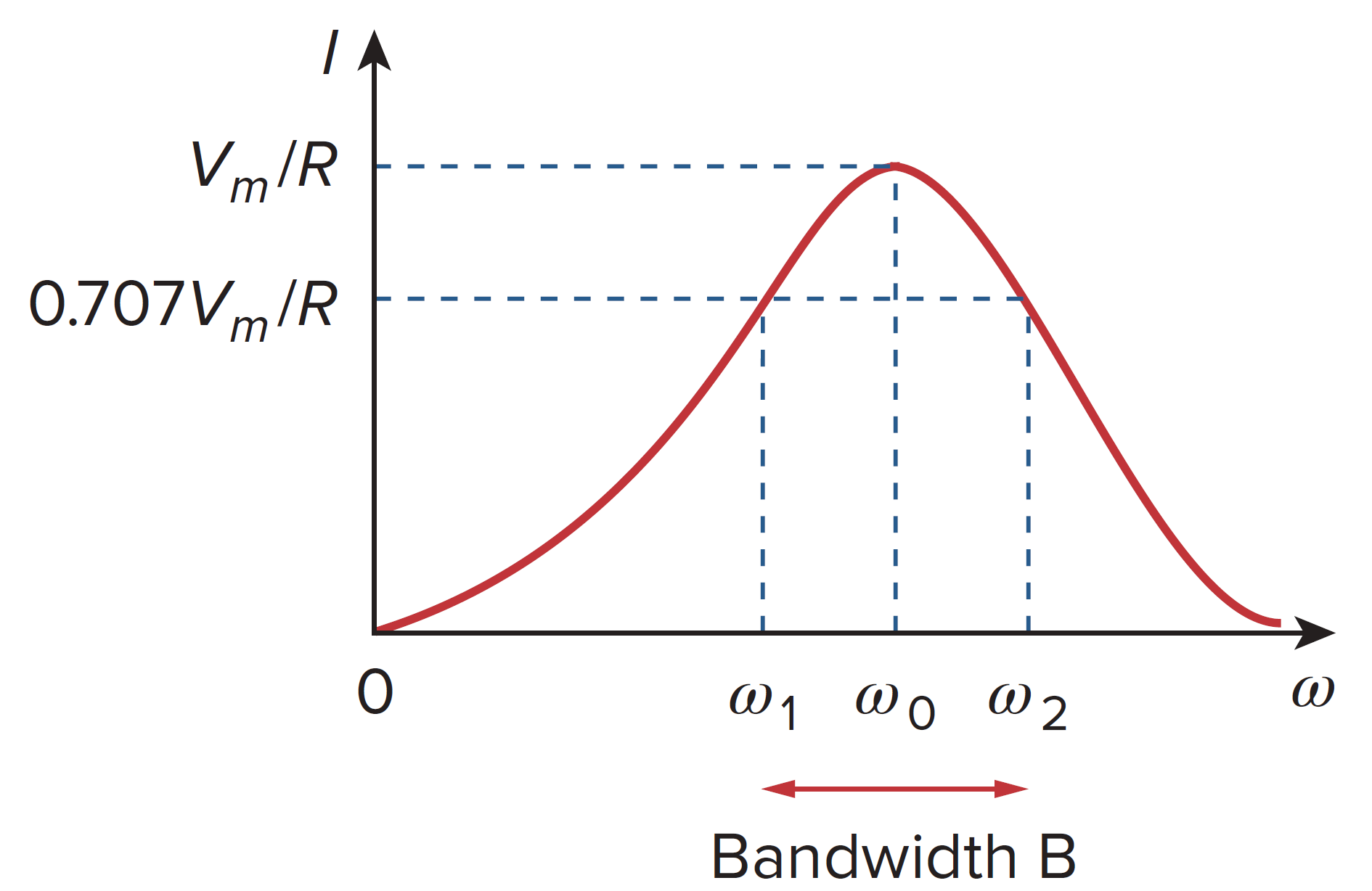
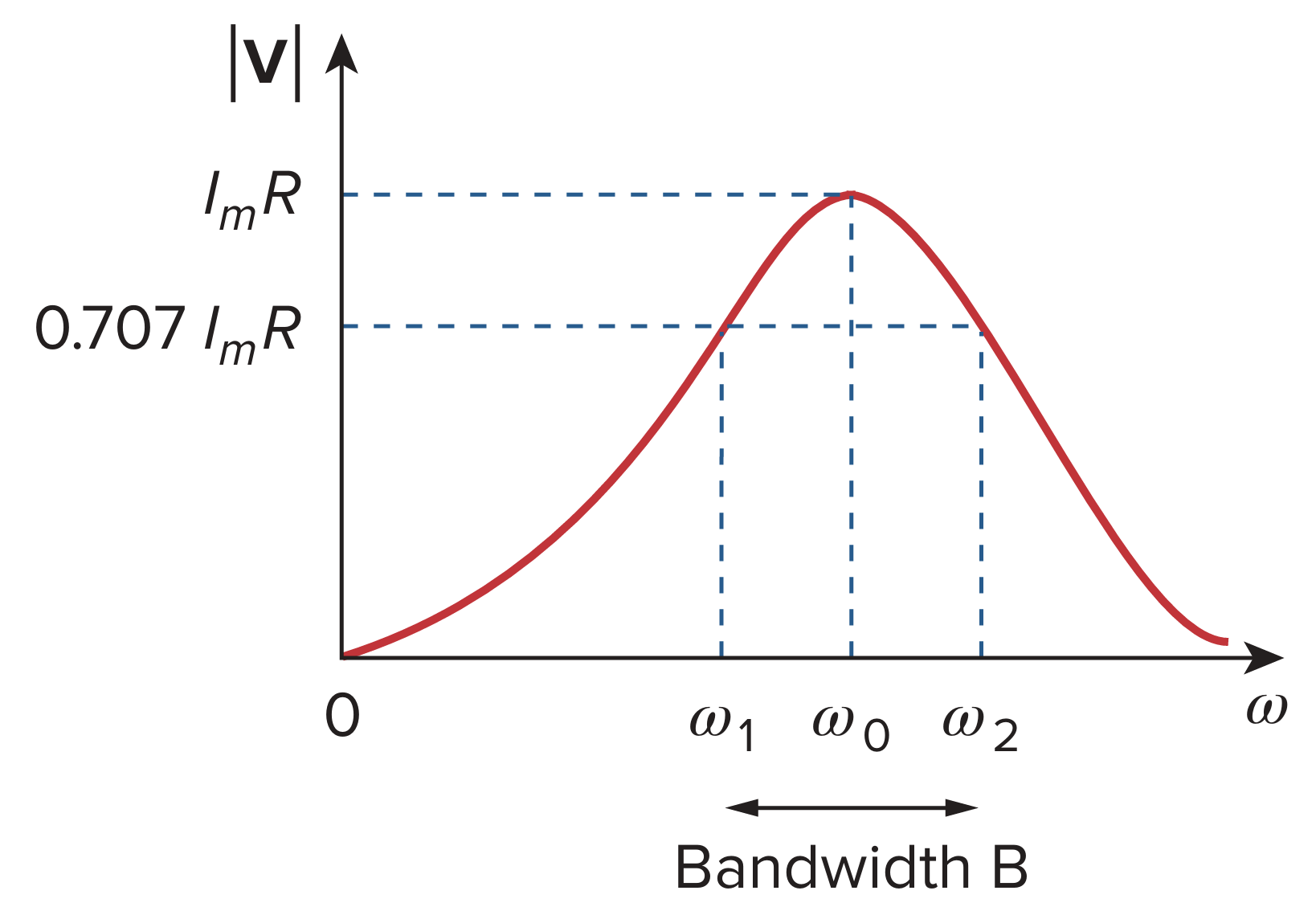
如图。

电路的电流幅值 I 的频率响应为 V_s / R

$$I=|\mathbf{I}|=\frac{V_m}{\sqrt{R^2+(\omega L-{\displaystyle \frac{1}{\omega C}{)}^2}}}$$

当 $\omega ={\omega }_0$ 时，电流幅值达到最大值 V_m / R。此时功率为

$$P({\omega }_0)=\frac{1}{2}\frac{V_m^2}{R}$$

${\omega }_1$ 和 ${\omega }_2$ 是电流幅值下降到最大值的一半时的频率。此时

$$P({\omega }_1)=P({\omega }_2)=\frac{1}{2}P({\omega }_0)=\frac{V_m^2}{4R}$$

因此，${\omega }_1$ 和 ${\omega }_2$ 也被称作半功率频率 (half-power frequencies)。注意到示意图中，仅在频率轴（横轴）为对数坐标时才显示出对称性。

为了求解半功率频率，令 $Z=\sqrt{2}R$ 即可

$$\sqrt{R^2+{(\omega L-{\displaystyle \frac{1}{\omega C}})}^2}=\sqrt{2}R$$

解得

$$\boxed{{\displaystyle \begin{array}{rl}{\omega }_1& =-\frac{R}{2L}+\sqrt{{\left(\frac{R}{2L}\right)}^2+\frac{1}{LC}}\\ {\omega }_2& =\frac{R}{2L}+\sqrt{{\left(\frac{R}{2L}\right)}^2+\frac{1}{LC}}\end{array}}}$$

将半功率频率与谐振频率联系起来

$${\omega }_0=\sqrt{{\omega }_1{\omega }_2}$$

带宽 (bandwidth) 被定义为半功率频率之间的差值

$$B={\omega }_2-{\omega }_1$$

严格来说，上述定义是半功率带宽。

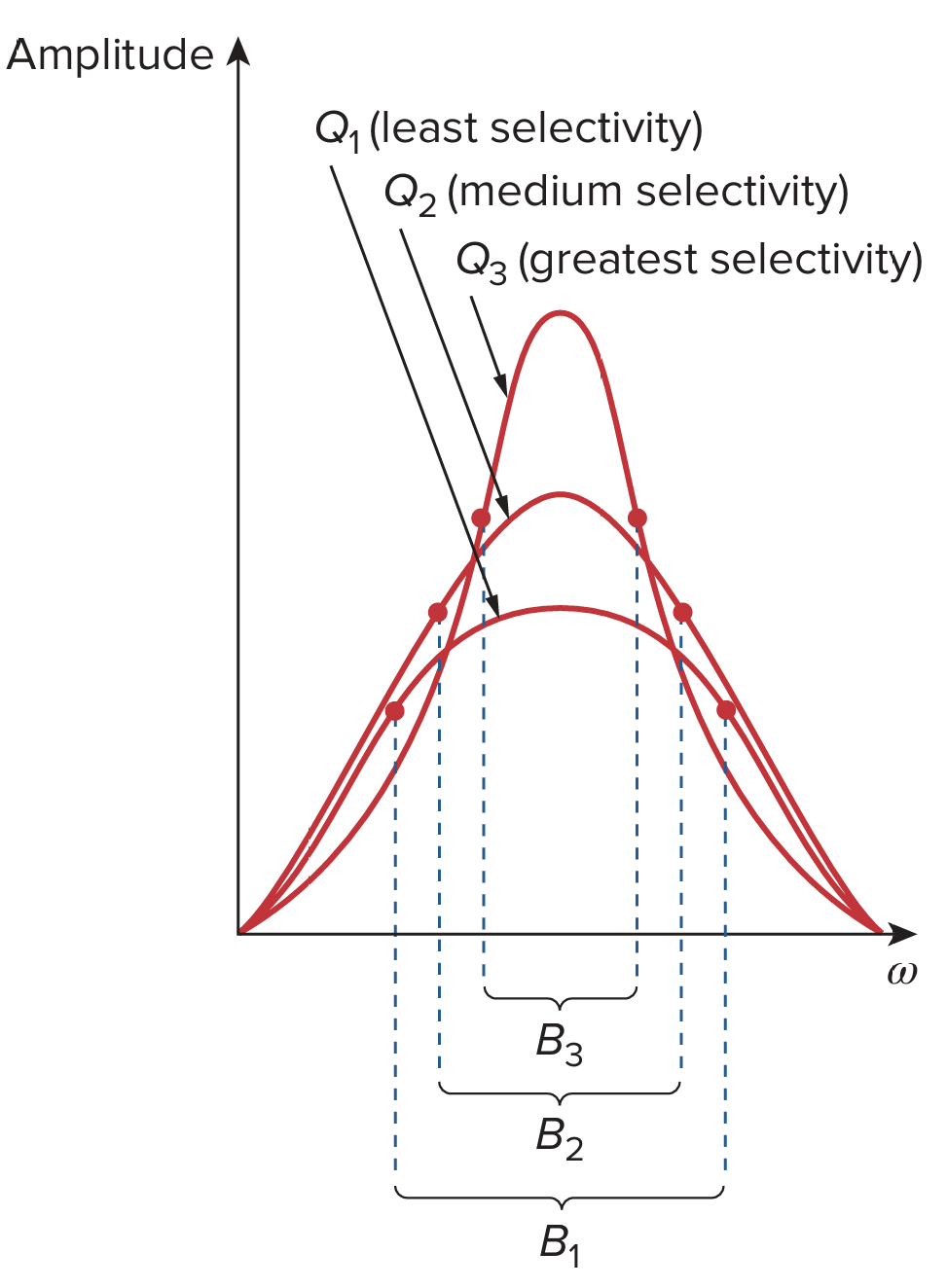
谐振电路中谐振的“尖锐程度”通过品质因数 (quality factor) Q 来定量测量。在谐振时，电路中的无功能量在电感和电容之间振荡。品质因数关联了存储的峰值能量与电路在每个振荡周期中消耗的能量

$$Q=2\pi \cdot \frac{\text{Peak energy stored in the circuit}}{\text{Energy dissipated by the circuit in one period at resonance}}$$

在串联 RLC 电路中，上述公式变为

$$Q=2\pi \frac{{\displaystyle \frac{1}{2}L{I}^2}}{{\displaystyle \frac{1}{2}{I}^{2}R{\displaystyle \frac{1}{f_0}}}}=\frac{2\pi f_{0}L}{R}$$

或

$$\boxed{{\displaystyle Q=\frac{{\omega }_{0}L}{R}=\frac{1}{{\omega }_{0}CR}}}$$

注意，品质因数是无量纲的。带宽 B 与品质因数 Q 的关系为

$$\boxed{{\displaystyle B=\frac{R}{L}={\omega }_0^{2}RC=\frac{{\omega }_0}{Q}}}$$

补充，谐振电路被设计为在其谐振频率或附近工作。当其品质因数等于或大于 10 时，称其为高 Q 电路。对于高 Q 电路 (Q ≥ 10)，半功率频率在所有实际应用中都围绕谐振频率对称，并且可以近似为

$${\omega }_1\approx {\omega }_0-\frac{B}{2},{\omega }_2\approx {\omega }_0+\frac{B}{2}$$

并联谐振

Parallel Resonance

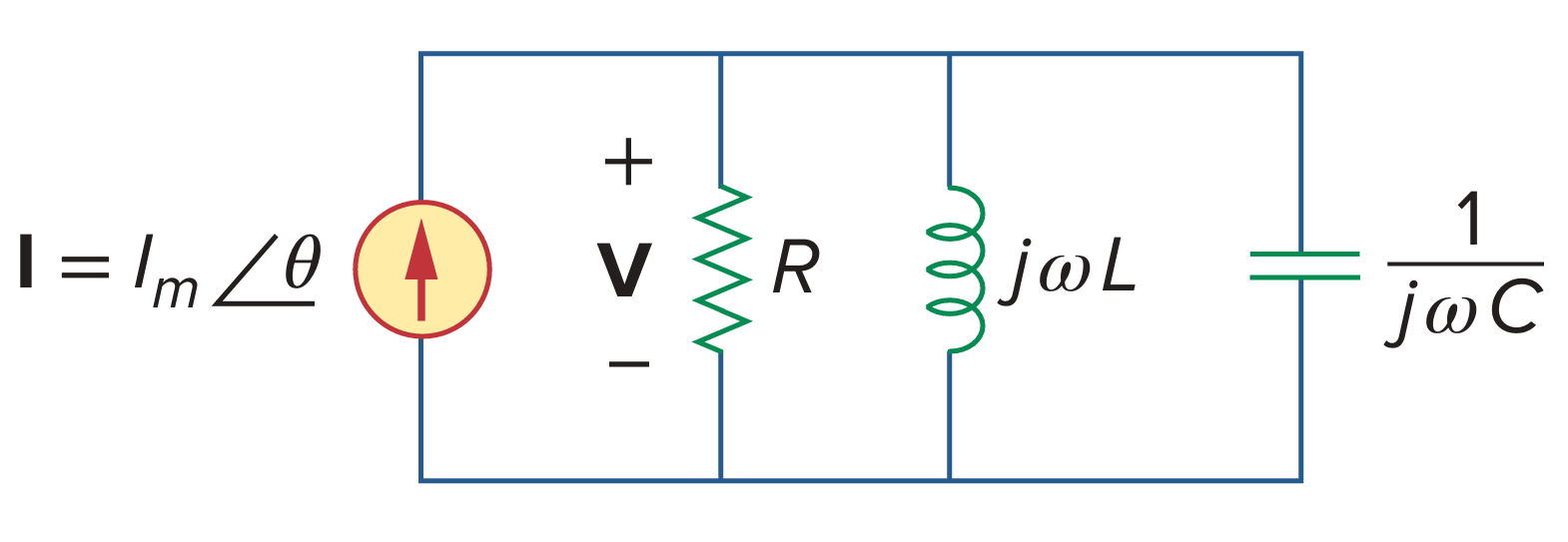
由于并联 RLC 电路和串联 RLC 电路是对偶的，因此可以避免不必要的重复计算。并联 RLC 电路的输入导纳为

$$\mathbf{Y}=\mathbf{H}(\omega )=\frac{\mathbf{I}}{\mathbf{V}}=\frac{1}{R}+j\omega C+\frac{1}{j\omega L}$$

或

$$\mathbf{Y}=\frac{1}{R}+j(\omega C-\frac{1}{\omega L})$$

当 Y 的虚部为零时，发生谐振

$$\omega C-\frac{1}{\omega L}=0$$

或

$$\boxed{{\displaystyle {\omega }_0=\frac{1}{\sqrt{LC}}\text{rad/s}}}$$

注意，在谐振时，并联 LC 组合的作用类似于开路，因此全部电流都流过 R。此外，在谐振时，电感和电容电流可能远大于源电流。

利用对偶性，使用 1/R、C、L 分别替换串联电路中的 R、L、C 即可得到并联电路的相应公式

$$\boxed{{\displaystyle \begin{array}{rl}{\omega }_1& =-\frac{1}{2RC}+\sqrt{{\left(\frac{1}{2RC}\right)}^2+\frac{1}{LC}}\\ {\omega }_2& =\frac{1}{2RC}+\sqrt{{\left(\frac{1}{2RC}\right)}^2+\frac{1}{LC}}\end{array}}}$$$$\boxed{{\displaystyle B={\omega }_2-{\omega }_1=\frac{1}{RC}}}$$$$\boxed{{\displaystyle Q=\frac{{\omega }_0}{B}={\omega }_{0}RC=\frac{R}{{\omega }_{0}L}}}$$

同样，对于高 Q 电路

$${\omega }_1\approx {\omega }_0-\frac{B}{2},{\omega }_2\approx {\omega }_0+\frac{B}{2}$$

Summary

滤波器

滤波器的四种理想频率响应图

无源

Passive Filters

低通

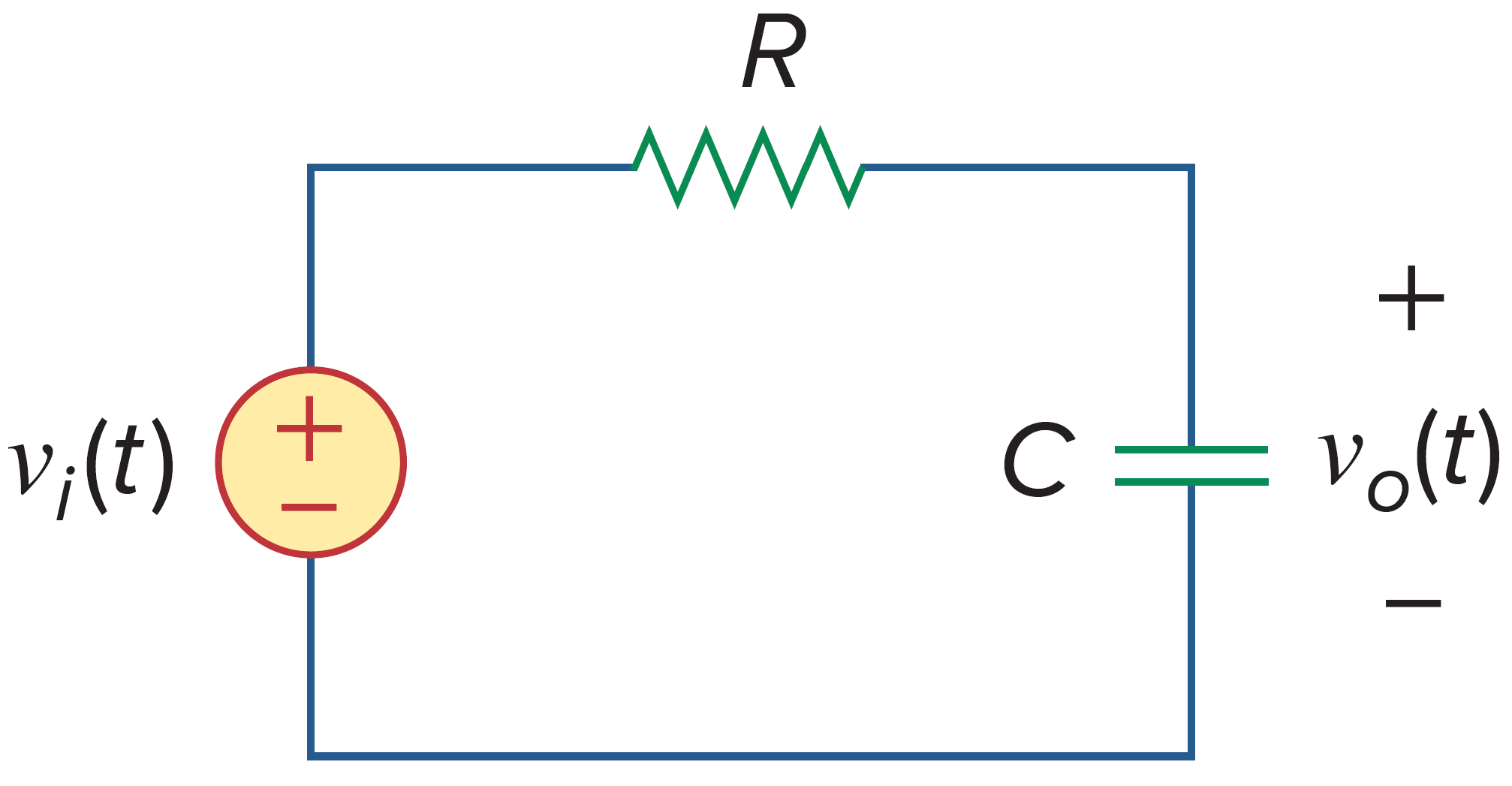
如图所示的 RC 串联电路即可实现最简单的低通滤波器。由输出电压和输入电压之比得到传递函数

$$\mathbf{H}(\omega )=\frac{{\mathbf{V}}_o}{{\mathbf{V}}_i}=\frac{1/j\omega C}{R+1/j\omega C}=\frac{1}{1+j\omega RC}$$

其满足 $\mathbf{H}(0)=1$ 和 $\mathbf{H}(\mathrm{\infty })=0$。

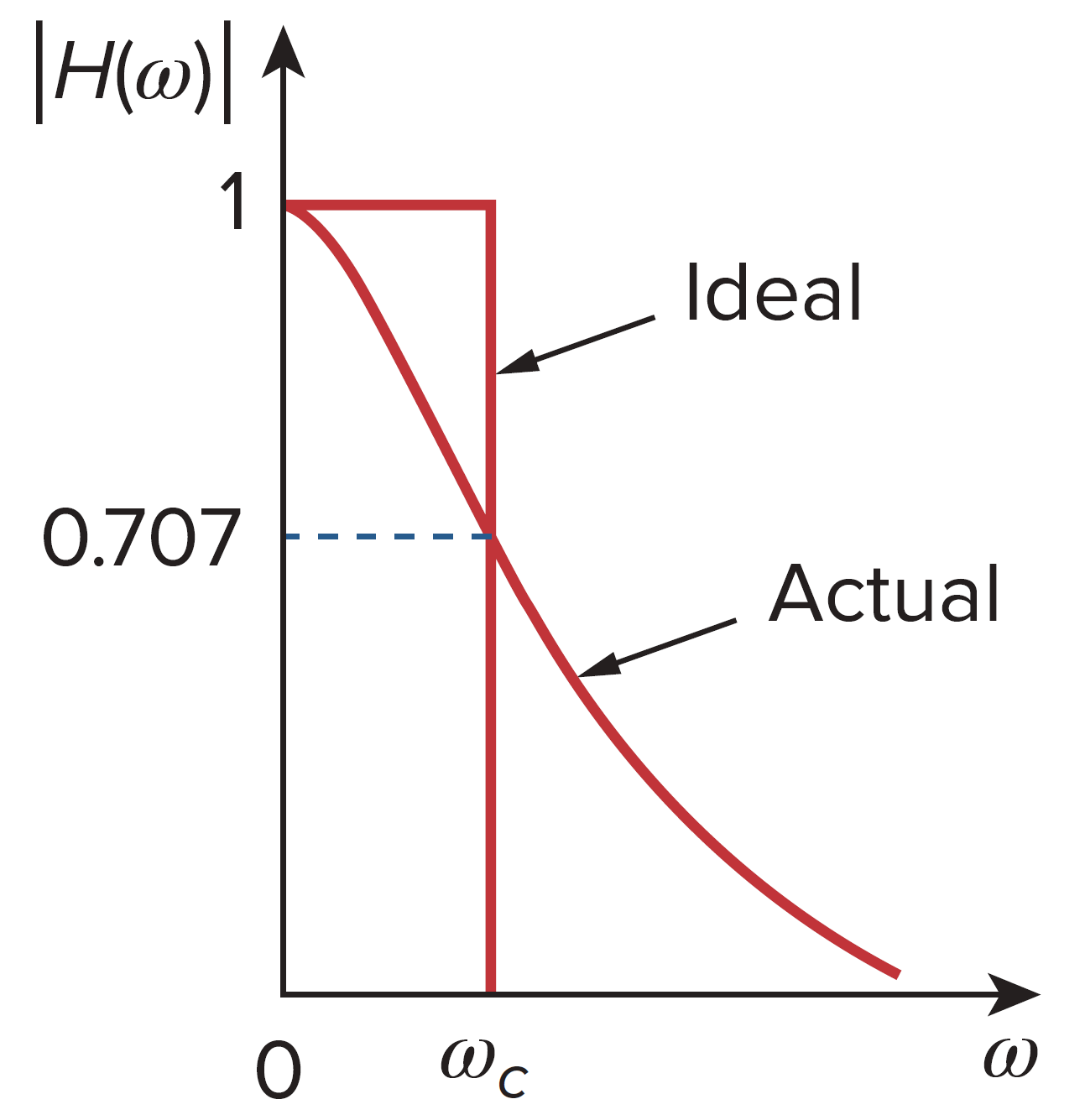
如图，半功率频率 (half-power frequency) 等于波特图中的转折频率 (corner frequency)，但在滤波器的语境中，它们通常被称为截止频率 (cutoff frequency)。它是通过将 $H(\omega )$ 的幅值设置为 $\frac{1}{\sqrt{2}}$ 来求解得到的。

$$H({\omega }_c)=\frac{1}{\sqrt{1+{\omega }_c^2{R}^2{C}^2}}=\frac{1}{\sqrt{2}}$$

或

$${\omega }_c=\frac{1}{RC}$$

低通滤波器也能通过 RL 电路实现。同时，低通滤波器还有更多种实现方式。

高通

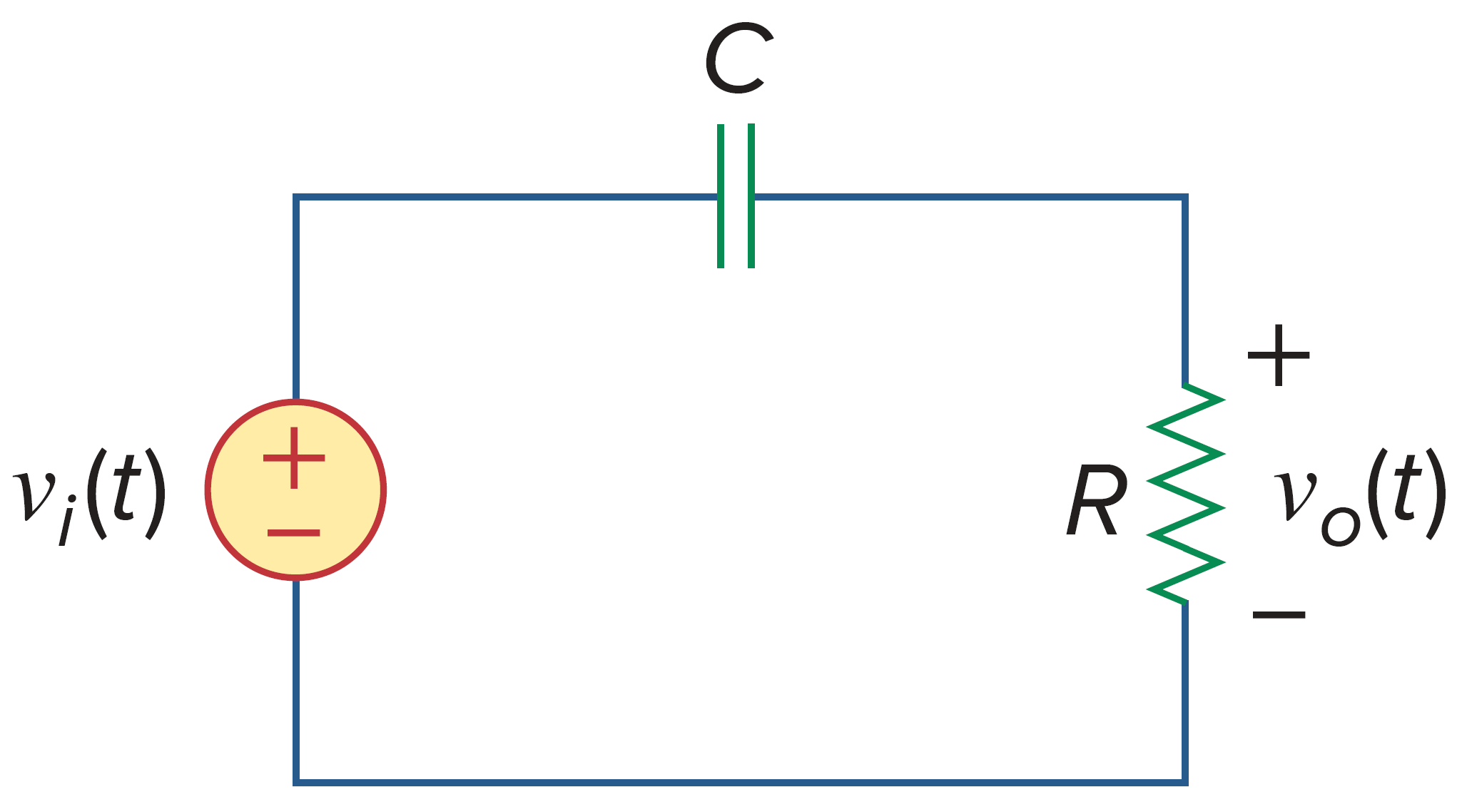
复用低通滤波器的示例电路，这次的输出电压为电阻 R 两端的电压。因此传递函数为

$$\mathbf{H}(\omega )=\frac{{\mathbf{V}}_o}{{\mathbf{V}}_i}=\frac{R}{R+1/j\omega C}=\frac{j\omega RC}{1+j\omega RC}$$

其满足 $\mathbf{H}(0)=0$ 和 $\mathbf{H}(\mathrm{\infty })=1$。

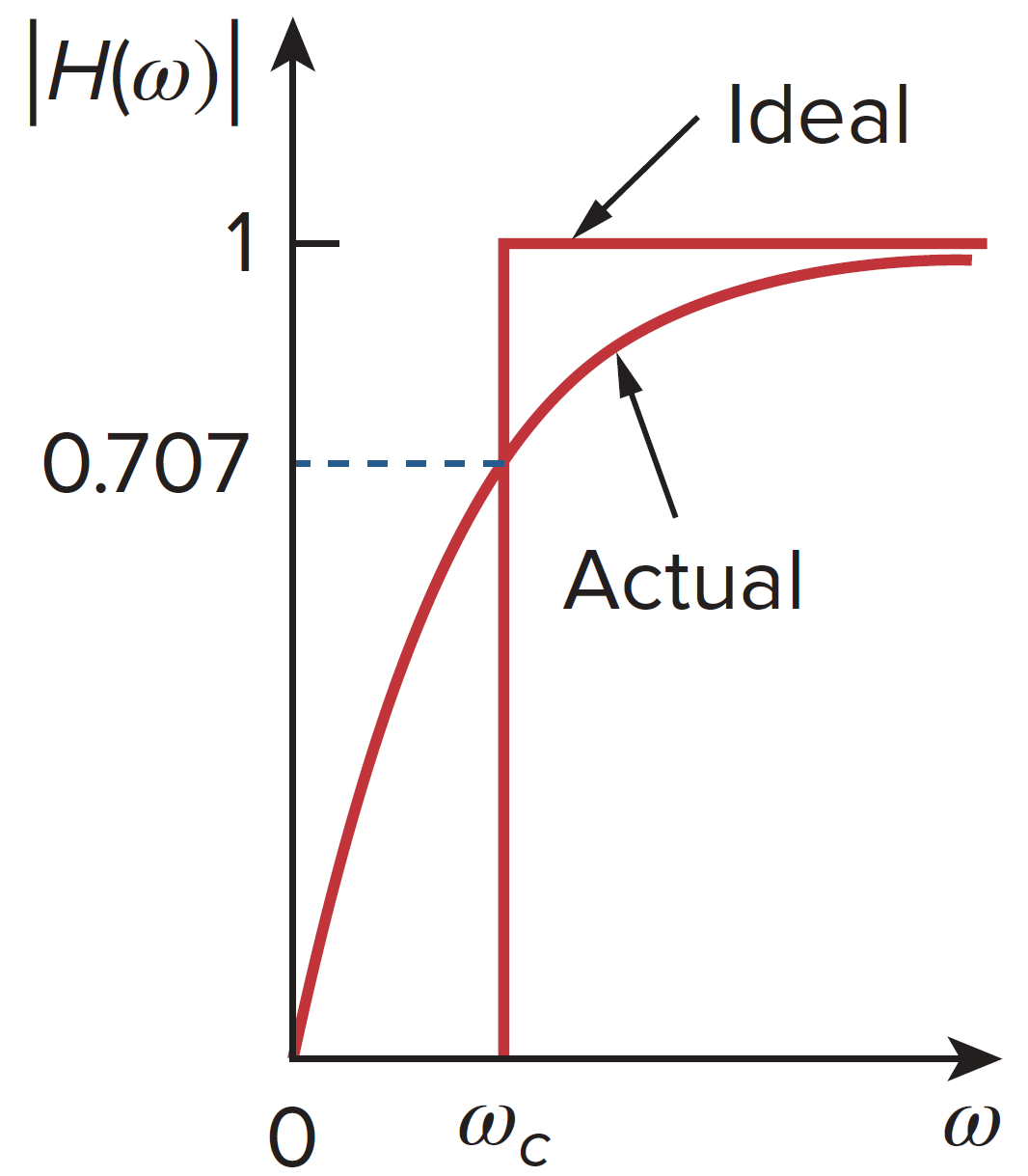
同理，它的截止频率为

$${\omega }_c=\frac{1}{RC}$$

高通滤波器也能通过 RC 电路实现。同时，高通滤波器还有更多种实现方式。

带通

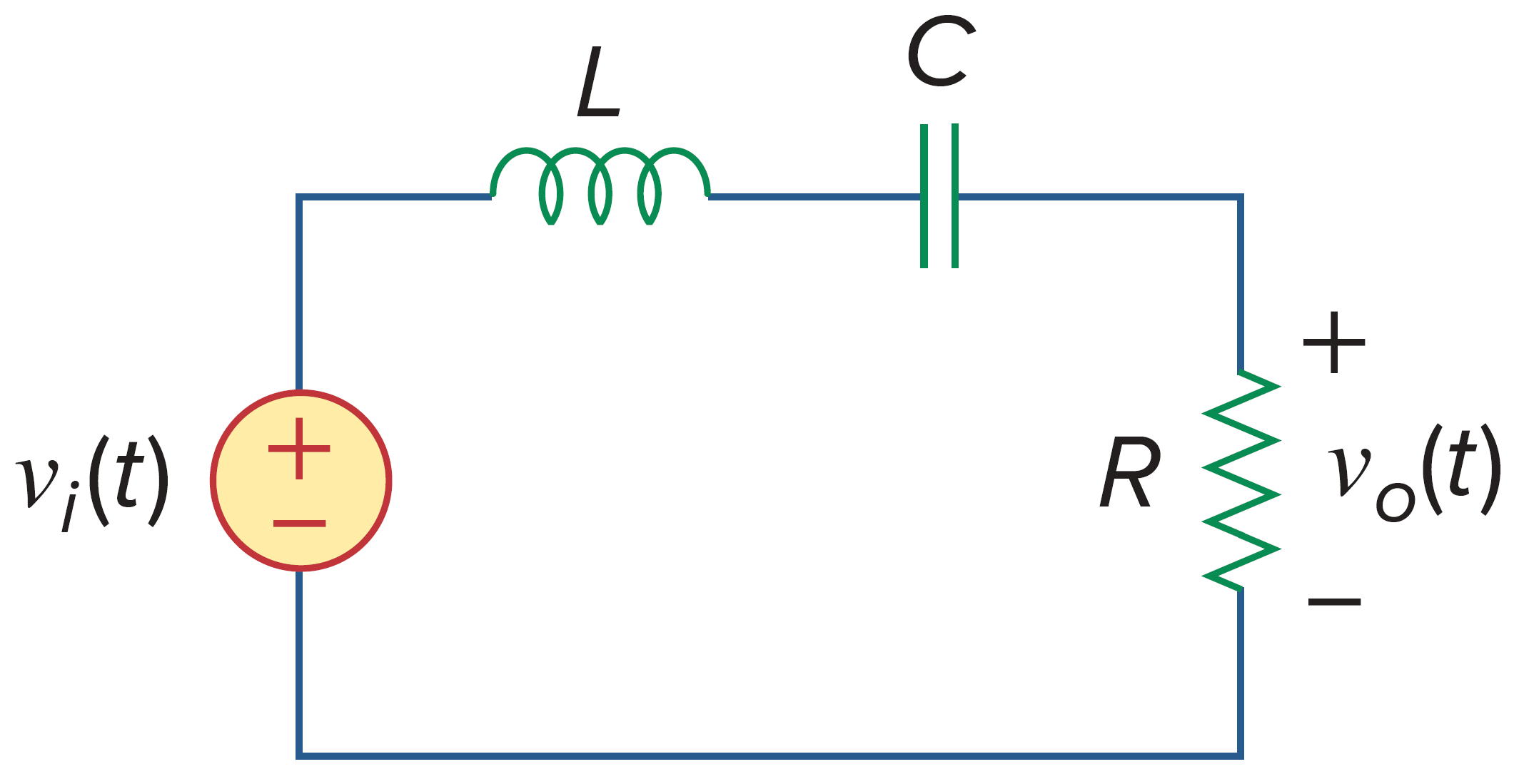
如图。这个 RLC 串联响应电路可以实现带通滤波器。其传递函数为

$$\mathbf{H}(\omega )=\frac{{\mathbf{V}}_o}{{\mathbf{V}}_i}=\frac{R}{R+j(\omega L-\frac{1}{\omega C})}$$

其满足 $\mathbf{H}(0)=0$ 和 $\mathbf{H}(\mathrm{\infty })=0$。

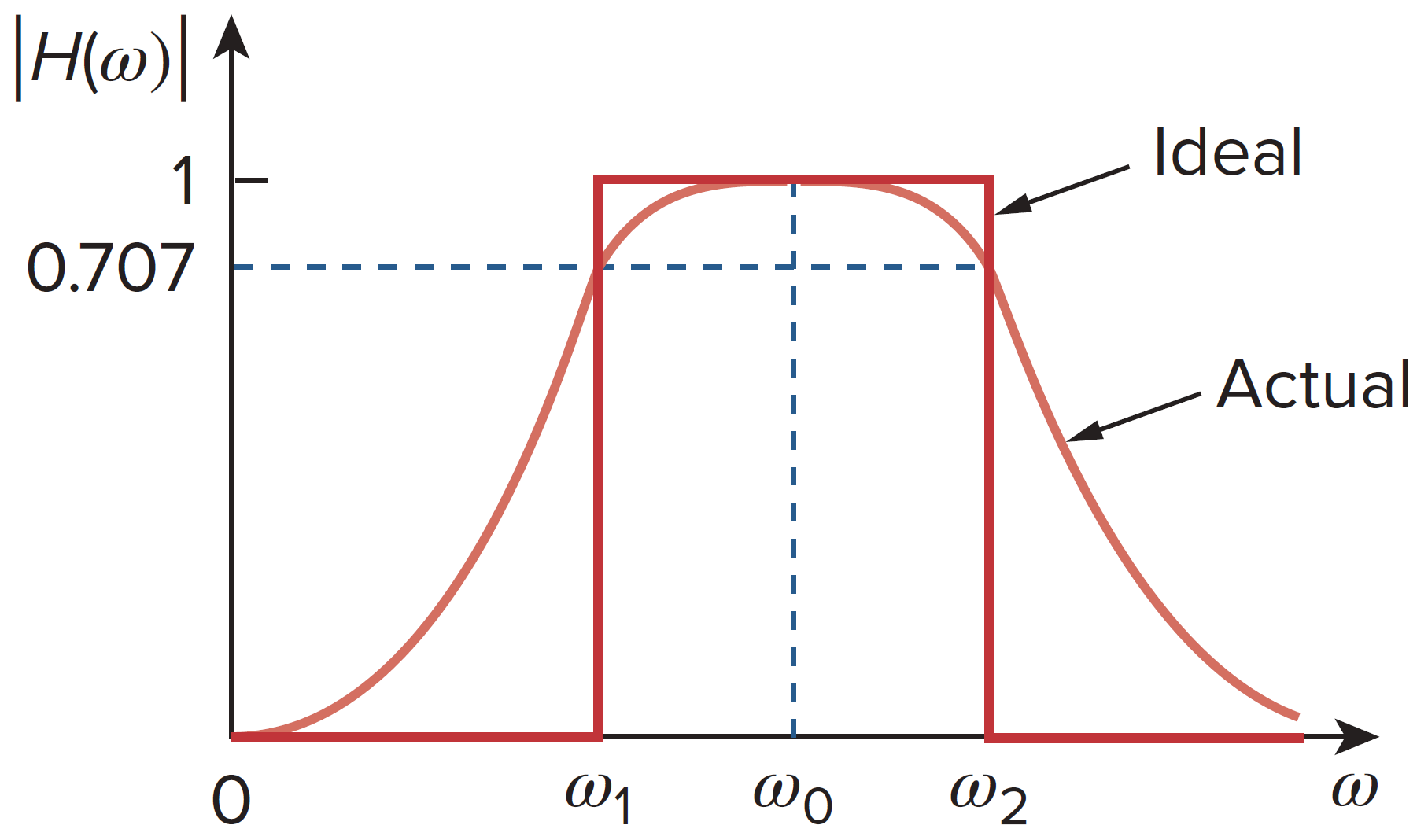
这个带通滤波器允许一个以 ω₀ 为中心的频率范围 (ω₁, ω₂) 的信号通过

$${\omega }_0=\frac{1}{\sqrt{LC}}$$

实际上，这个带通滤波器的电路模型在之前的串联谐振中已经介绍过了。其半功率频率、带宽和品质因数参考谐振电路的公式即可。

带阻

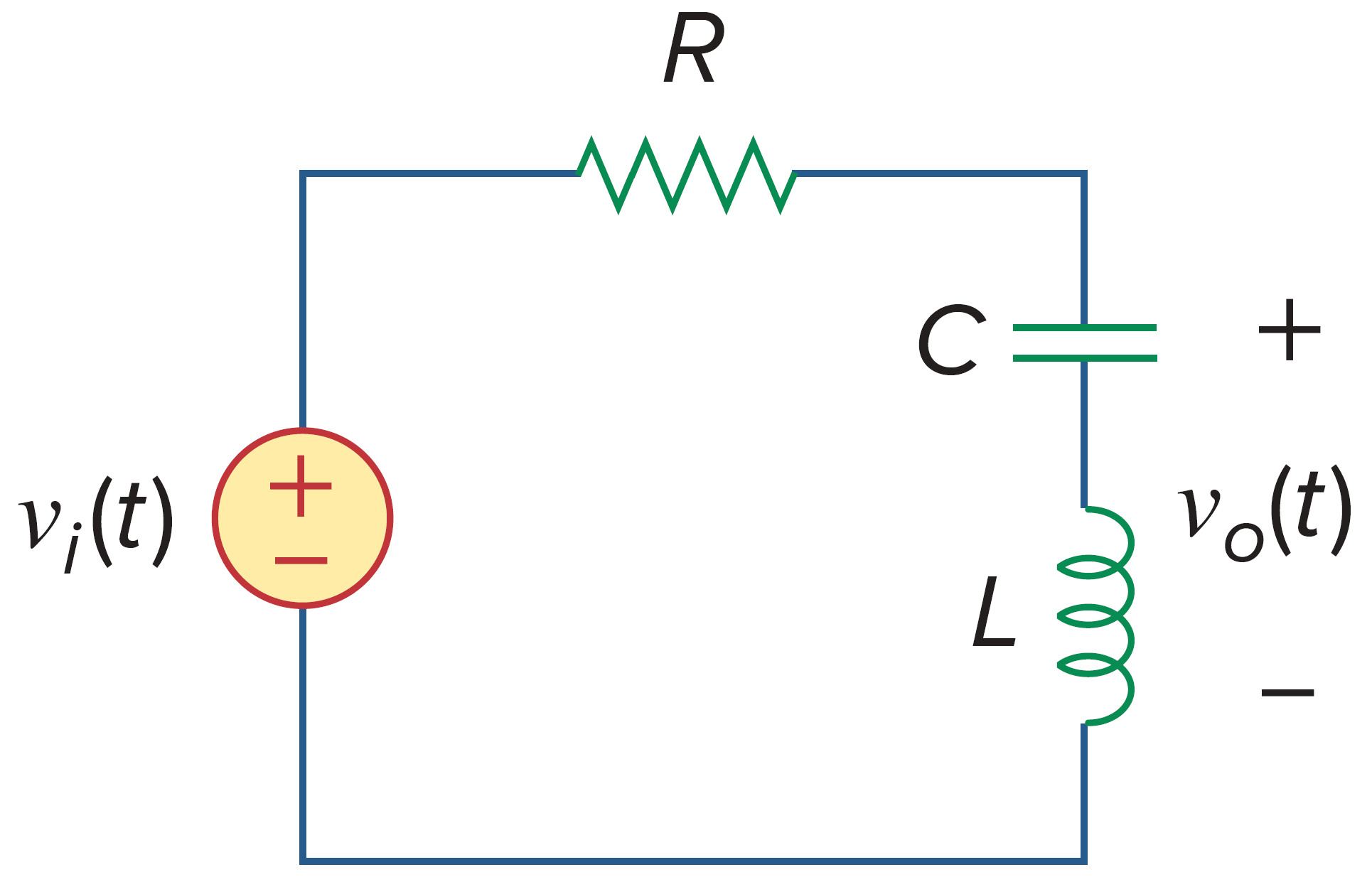
如图，传递函数为

$$\mathbf{H}(\omega )=\frac{{\mathbf{V}}_o}{{\mathbf{V}}_i}=\frac{j(\omega L-1/\omega C)}{R+j(\omega L-1/\omega C)}$$

其满足 $\mathbf{H}(0)=1$ 和 $\mathbf{H}(\mathrm{\infty })=1$。

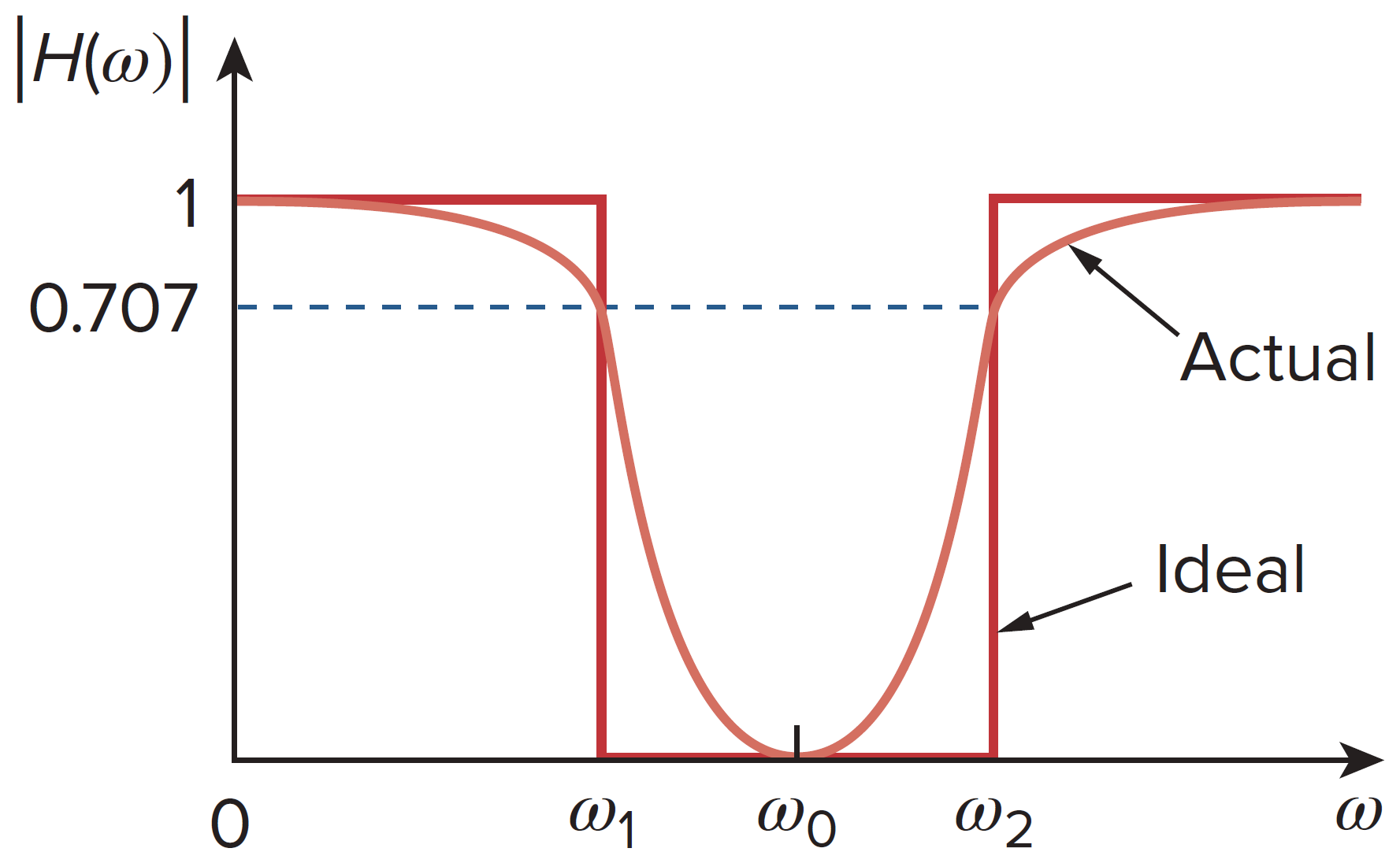
抑制频率 (the frequency of rejection) 为

$${\omega }_0=\frac{1}{\sqrt{LC}}$$

Conclusion

1. 无源滤波器 (passive filters) 的最大增益为 1 (unity)。要产生大于 1 的增益，应该使用有源滤波器 (active filters)。
2. 还有很多其他更复杂的拓扑结构 (topologies) 也能实现本文讨论的四种滤波器。
3. 本文讨论的滤波器都是极其简单的。许多其他的滤波器具有更尖锐 (sharper) 和更复杂 (complex) 的频率响应。

有源

Active Filters

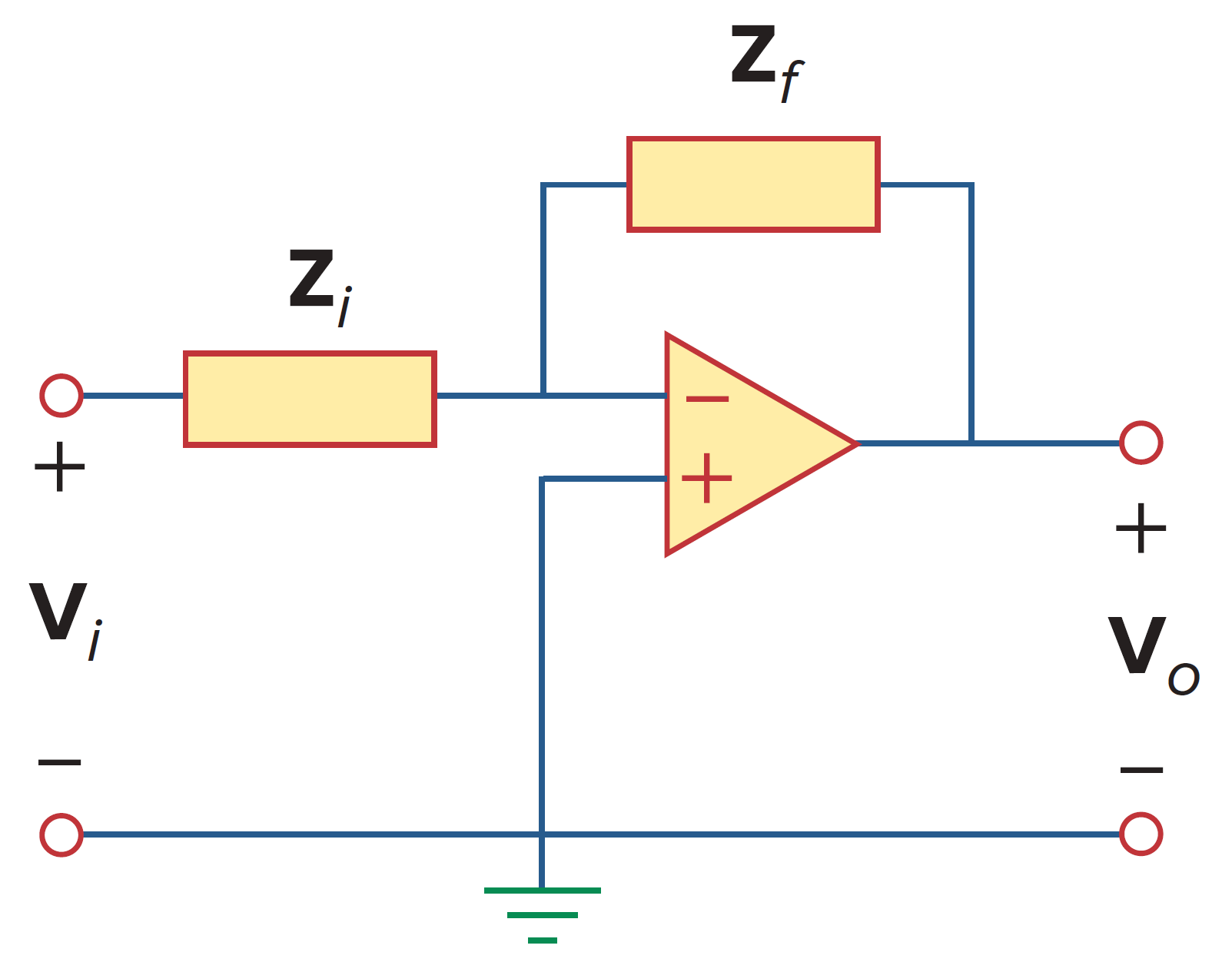
一阶低通

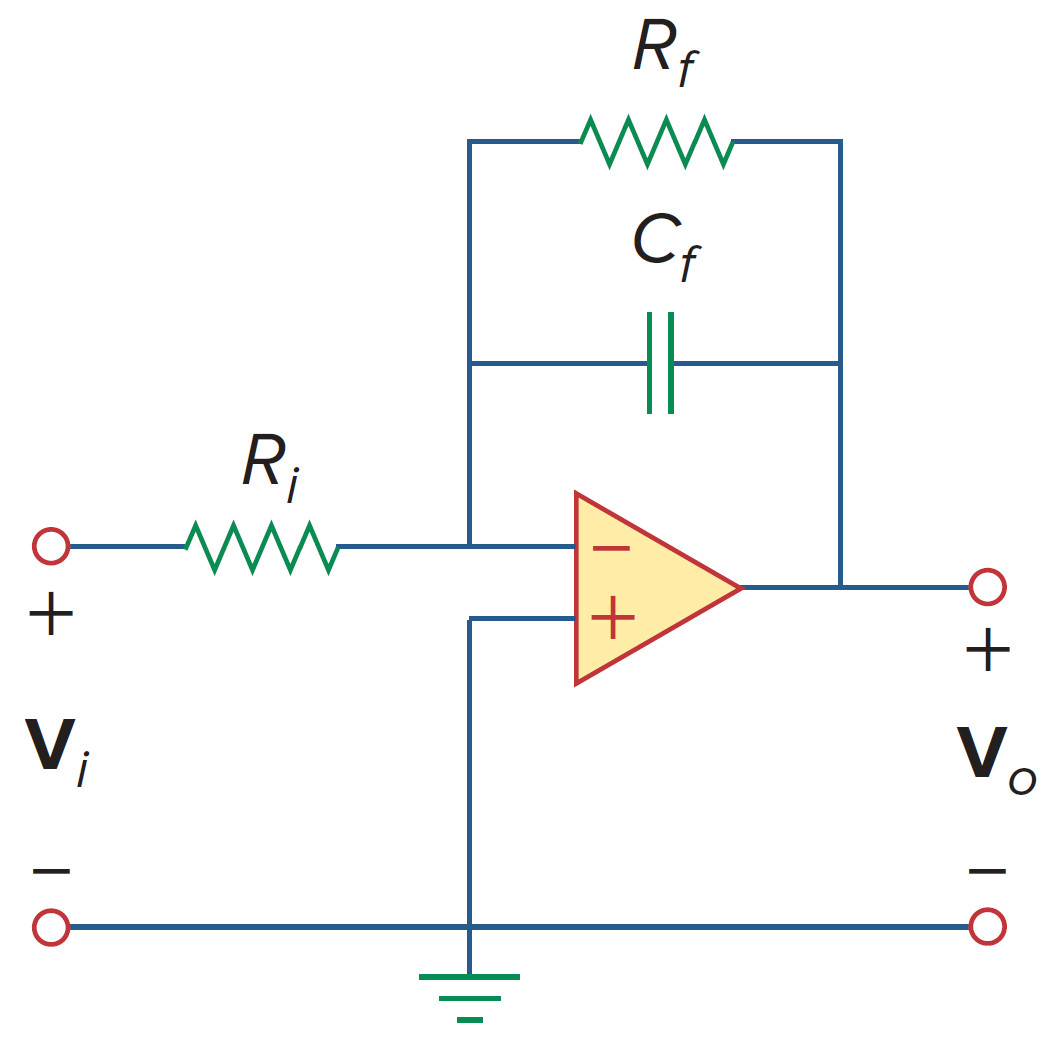
如上图所示，这是一个典型的有源低通滤波器。其传递函数为

$$\mathbf{H}(\omega )=\frac{{\mathbf{V}}_o}{{\mathbf{V}}_i}=-\frac{{\mathbf{Z}}_f}{{\mathbf{Z}}_i}$$

其中，

$${\mathbf{Z}}_i=R_i,{\mathbf{Z}}_f=R_f\parallel \frac{1}{j\omega C_f}=\frac{R_f}{1+j\omega R_f{C}_f}$$

于是，

$$\mathbf{H}(\omega )=-\frac{\frac{R_f}{1+j\omega R_f{C}_f}}{R_i}=-\frac{R_f}{R_i}\cdot \frac{1}{1+j\omega R_f{C}_f}$$

并且，$\mathbf{H}(0)=-R_f/R_i$ 和 $\mathbf{H}(\mathrm{\infty })=0$。

该滤波器的简单极点 $p_1$ 位于 $s=-\frac{1}{R_f{C}_f}$。

其截止频率 ${\omega }_c$ 由该极点的位置决定，也就是

$${\omega }_c=|p_1|=\frac{1}{R_f{C}_f}$$

注意到，截止频率 ${\omega }_c$ 由电阻 $R_f$ 和电容 $C_f$ 决定，与电阻 $R_i$ 无关。这意味着如果有需要，可以将多个具有不同输入电阻 $R_i$ 的输入信号相加，而每个输入的截止频率保持相同。

一阶高通

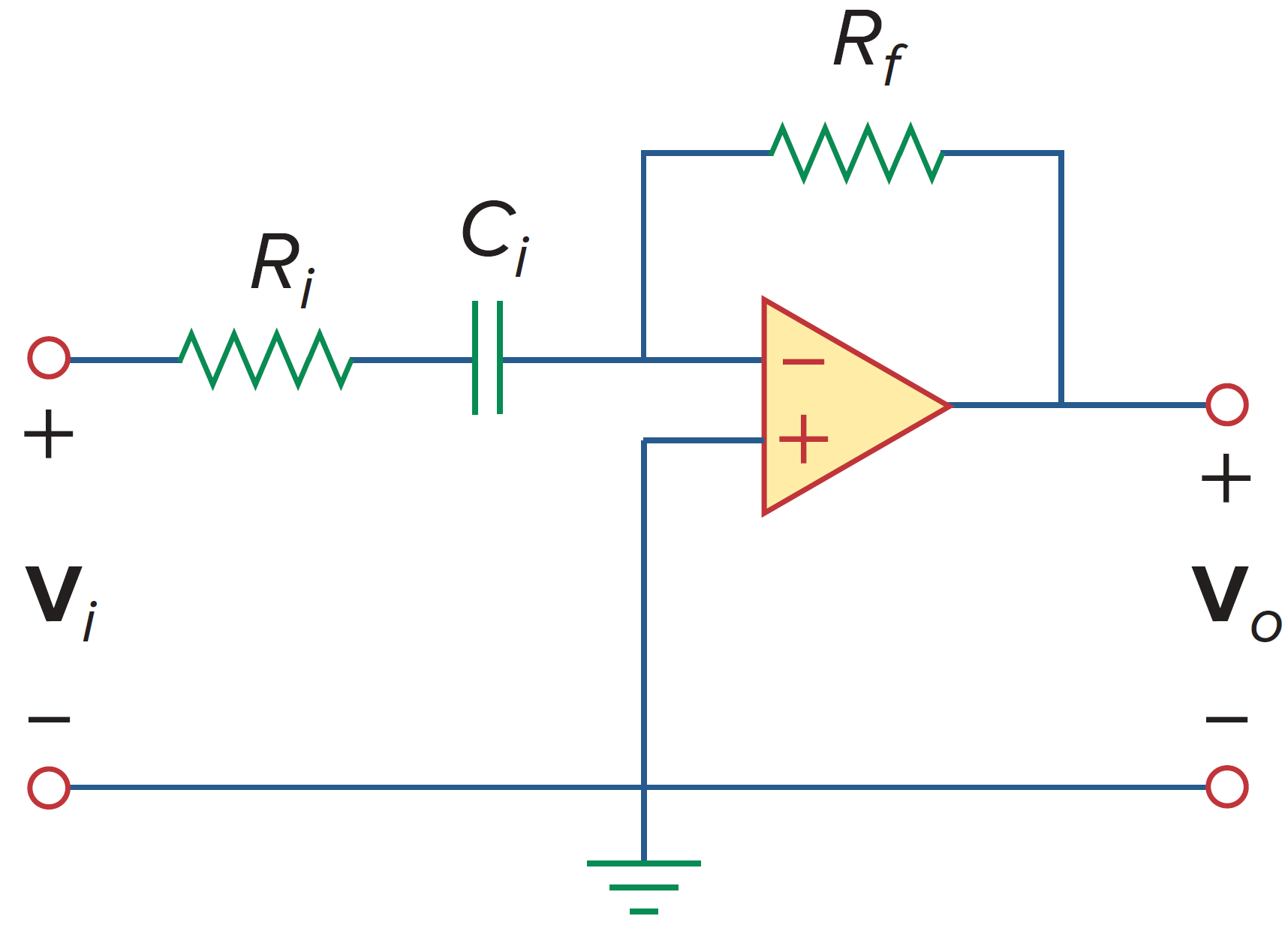
如上图所示，这是一个典型的有源高通滤波器。其传递函数为

$$\mathbf{H}(\omega )=\frac{{\mathbf{V}}_o}{{\mathbf{V}}_i}=-\frac{{\mathbf{Z}}_f}{{\mathbf{Z}}_i}$$

其中，

$${\mathbf{Z}}_i=R_i+1/j\omega C_i,{\mathbf{Z}}_f=R_f$$

于是，

$$\mathbf{H}(\omega )=-\frac{R_f}{R_i+1/j\omega C_i}=-\frac{j\omega R_f{C}_i}{1+j\omega R_i{C}_i}$$

并且，$\mathbf{H}(0)=0$ 和 $\mathbf{H}(\mathrm{\infty })=-R_f/R_i$。

该滤波器的简单极点 $p_1$ 位于 $s=-\frac{1}{R_i{C}_i}$。

其截止频率 ${\omega }_c$ 为

$${\omega }_c=\frac{1}{R_i{C}_i}$$

带通

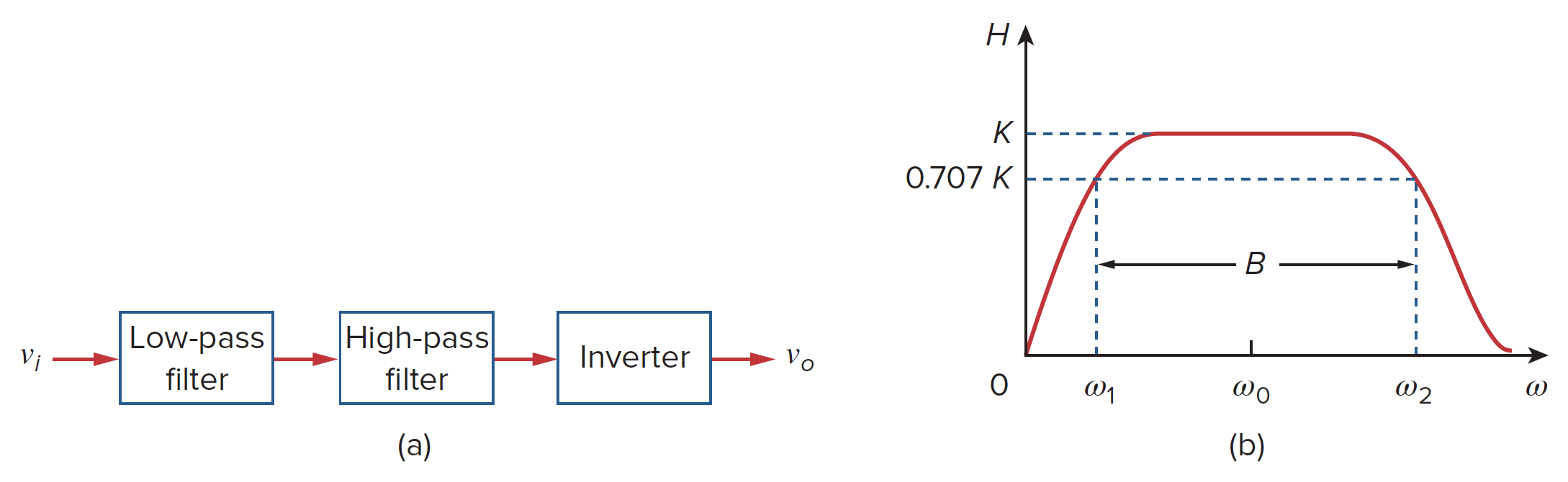
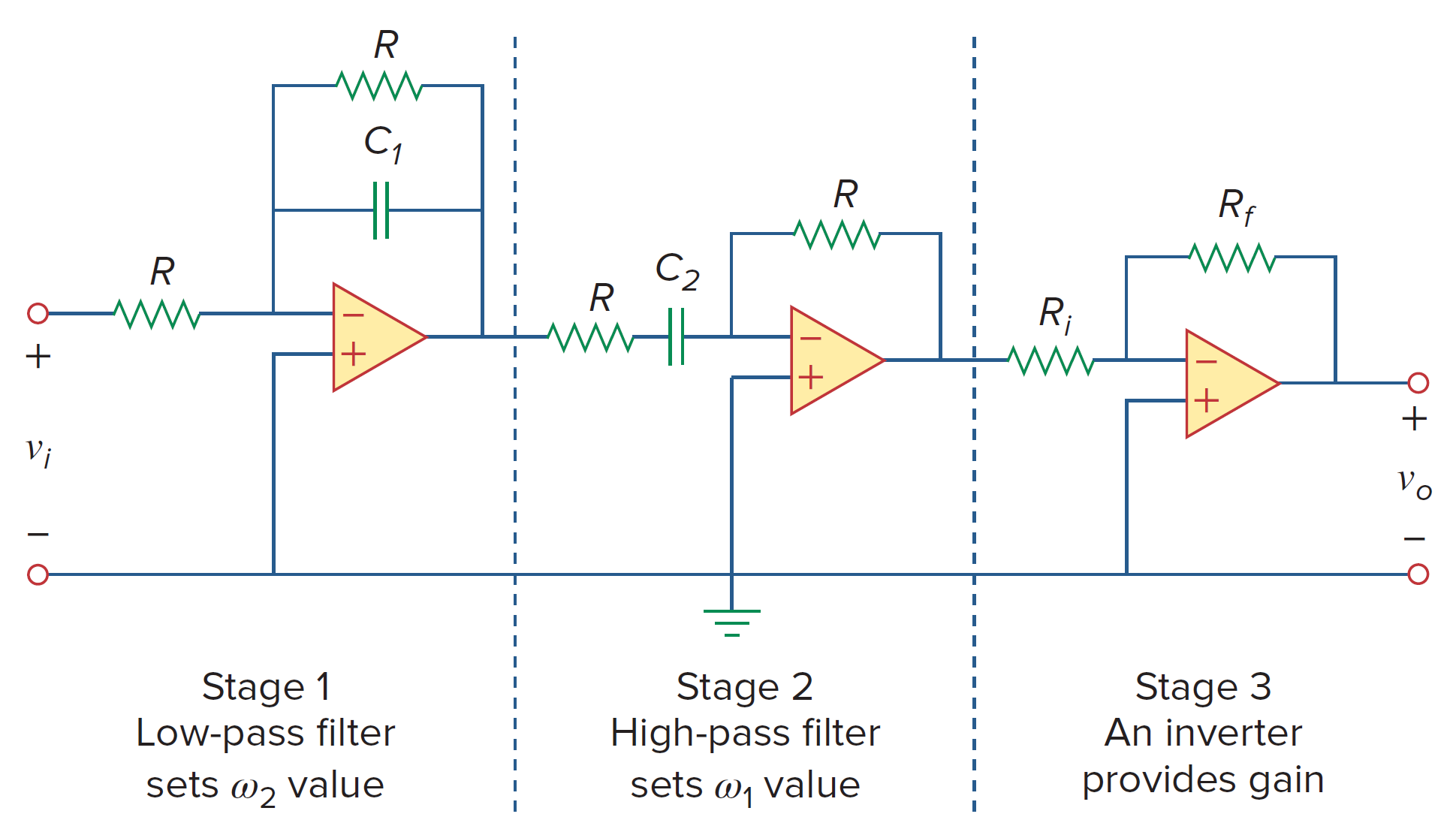
如上图所示，其传递函数为

$$\begin{array}{rl}\mathbf{H}(\omega )=\frac{{\mathbf{V}}_o}{{\mathbf{V}}_i}& =(-\frac{1}{1+j\omega C_{1}R})(-\frac{j\omega C_{2}R}{1+j\omega C_{2}R})(-\frac{R_f}{R_i})\\ & =-\frac{R_f}{R_i}\cdot \frac{1}{1+j\omega C_{1}R}\cdot \frac{j\omega C_{2}R}{1+j\omega C_{2}R}\end{array}$$

低通部分提供了上截止频率 (the upper corner frequency)

$${\omega }_2=\frac{1}{R{C}_1}$$

而高通部分提供了下截止频率 (the lower corner frequency)

$${\omega }_1=\frac{1}{R{C}_2}$$

因此，整体电路的中心频率 (the center frequency)、带宽、品质因数分别为

$$\begin{array}{rl}{\omega }_0& =\sqrt{{\omega }_1{\omega }_2}\\ B& ={\omega }_2-{\omega }_1\\ Q& =\frac{{\omega }_0}{B}\end{array}$$

为了得到带通的增益 K，将传递函数表示为其标准形式

$$\mathbf{H}(\omega )=-\frac{R_f}{R_i}\cdot \frac{j\omega /{\omega }_1}{(1+j\omega /{\omega }_1)(1+j\omega /{\omega }_2)}$$

传递函数的模长为

$$|\mathbf{H}({\omega }_0)|=|\frac{R_f}{R_i}\cdot \frac{j{\omega }_0/{\omega }_2}{({\omega }_1+j{\omega }_0)({\omega }_2+j{\omega }_0)}|=\frac{R_f}{R_i}\cdot \frac{{\omega }_2}{{\omega }_1+{\omega }_2}$$

因此，增益为

$$K=\frac{R_f}{R_i}\cdot \frac{{\omega }_2}{{\omega }_1+{\omega }_2}$$

带阻

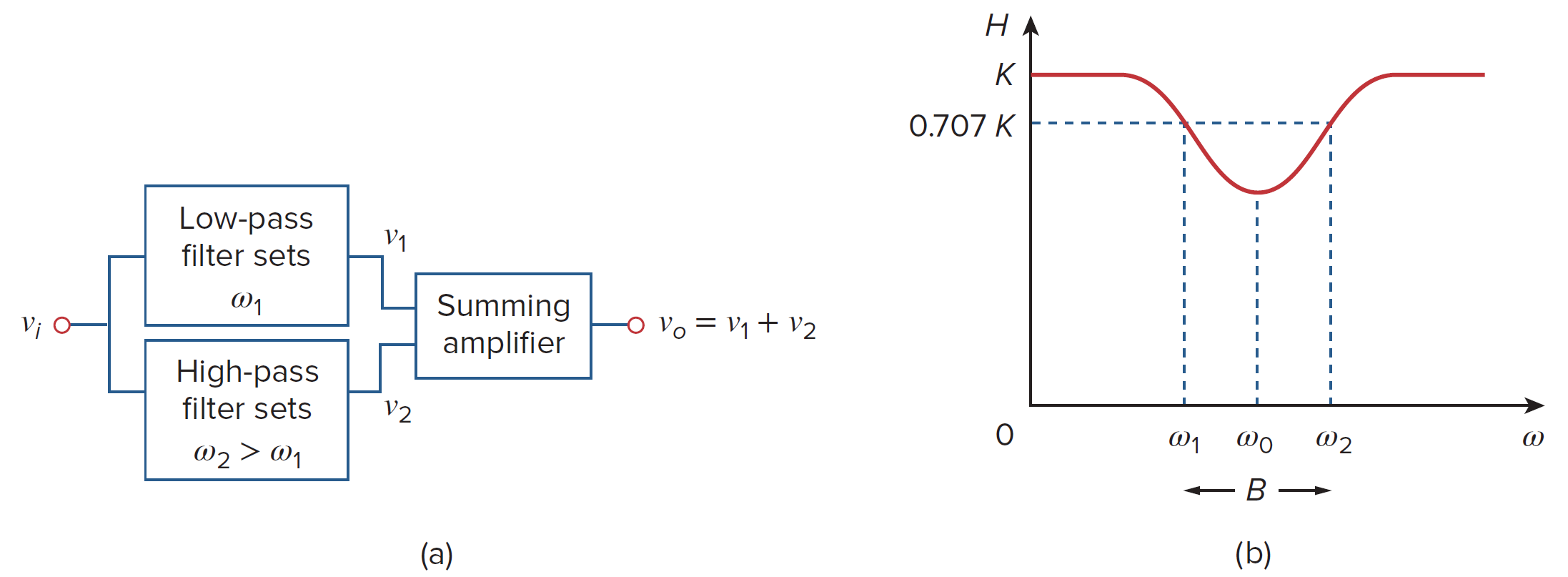
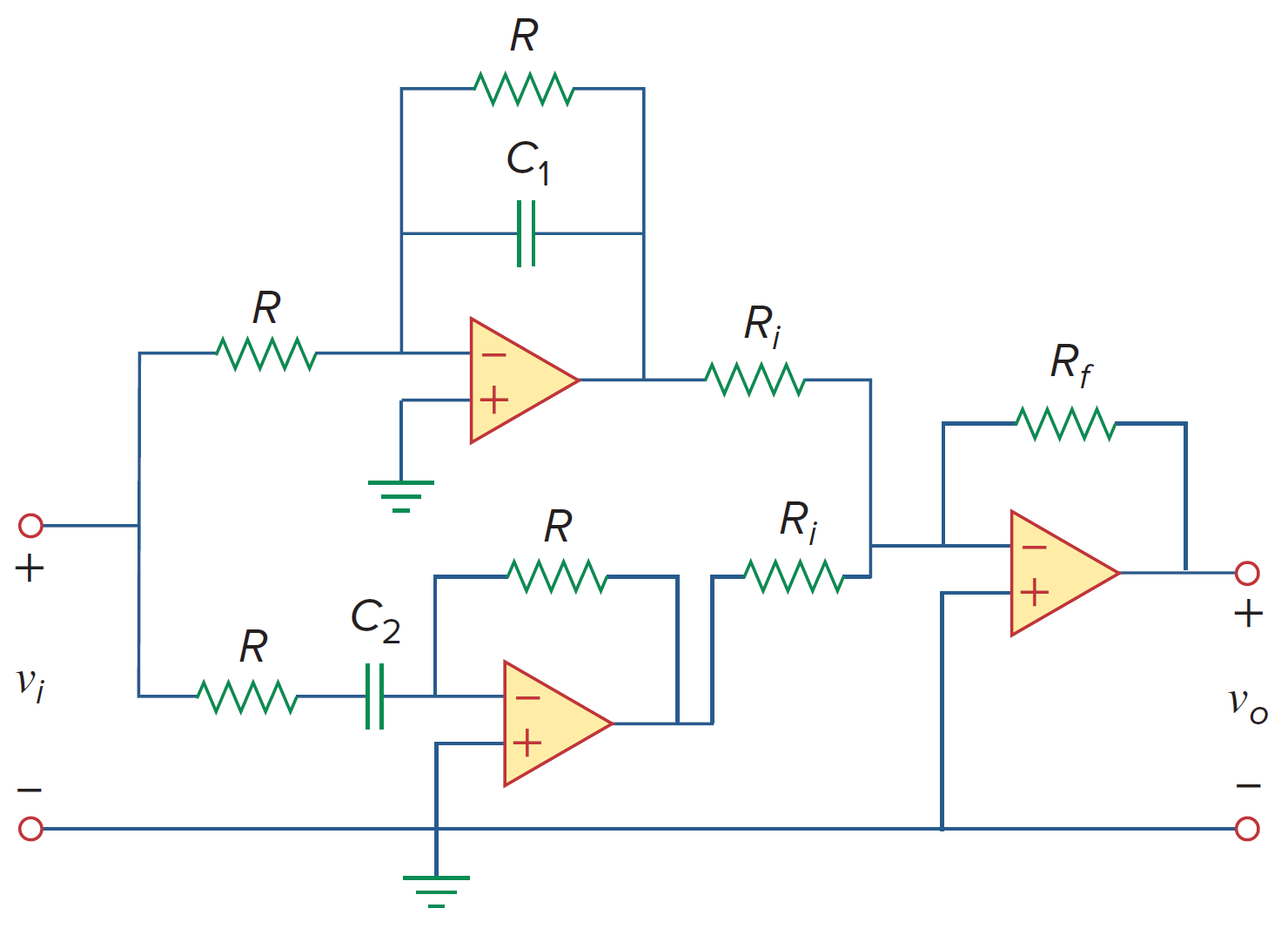
带阻滤波器可以通过将一个低通滤波器和一个高通滤波器并联，并连接到一个反向加法放大器来构建。

如上图所示，其传递函数为

$$\begin{array}{rl}\mathbf{H}(\omega )=\frac{{\mathbf{V}}_o}{{\mathbf{V}}_i}& =-\frac{R_f}{R_i}(-\frac{1}{1+j\omega C_{1}R}-\frac{j\omega C_{2}R}{1+j\omega C_{2}R})\\ & =\frac{R_f}{R_i}\cdot \frac{(1+j2\omega /{\omega }_1+(j\omega {)}^2/{\omega }_1{\omega }_1)}{(1+j\omega /{\omega }_2)(1+j\omega /{\omega }_1)}\end{array}$$

中心频率 ${\omega }_0$ 处的增益为

$$K=H({\omega }_0)=\frac{R_f}{R_i}\cdot \frac{2{\omega }_1}{{\omega }_1+{\omega }_2}$$

这里出现的有源滤波器们，都是很简单的实现方案。实际上，还有更多更复杂的实现方案。

比例变换

Scaling

幅值变换

Magnitude Scaling

$$\begin{array}{rl}{R}^{\prime }& =K_{m}R\\ L^{\prime }& =K_{m}L\\ C^{\prime }& =K_{m}C\\ {\omega }^{\prime }& =\omega \end{array}$$

频率变换

Frequency Scaling

$$\begin{array}{rl}{R}^{\prime }& =R\\ L^{\prime }& =\frac{L}{K_f}\\ C^{\prime }& =\frac{C}{K_f}\\ {\omega }^{\prime }& =K_f\omega \end{array}$$

幅值和频率变换

$$\begin{array}{rl}{R}^{\prime }& =K_{m}R\\ L^{\prime }& =K_{m}L\\ C^{\prime }& =K_{m}C\\ {\omega }^{\prime }& =K_f\omega \end{array}$$