内力
内载荷
Internal Loadings
Internal loadings are determined by using the method of sections.
在应用截面法时,习惯上分析整体的左半侧。(将体现在示例中的受力分析中)
基本概念
二维情况下,通常只考虑以下三种力:(如图)
normal force
shear force
bending moment
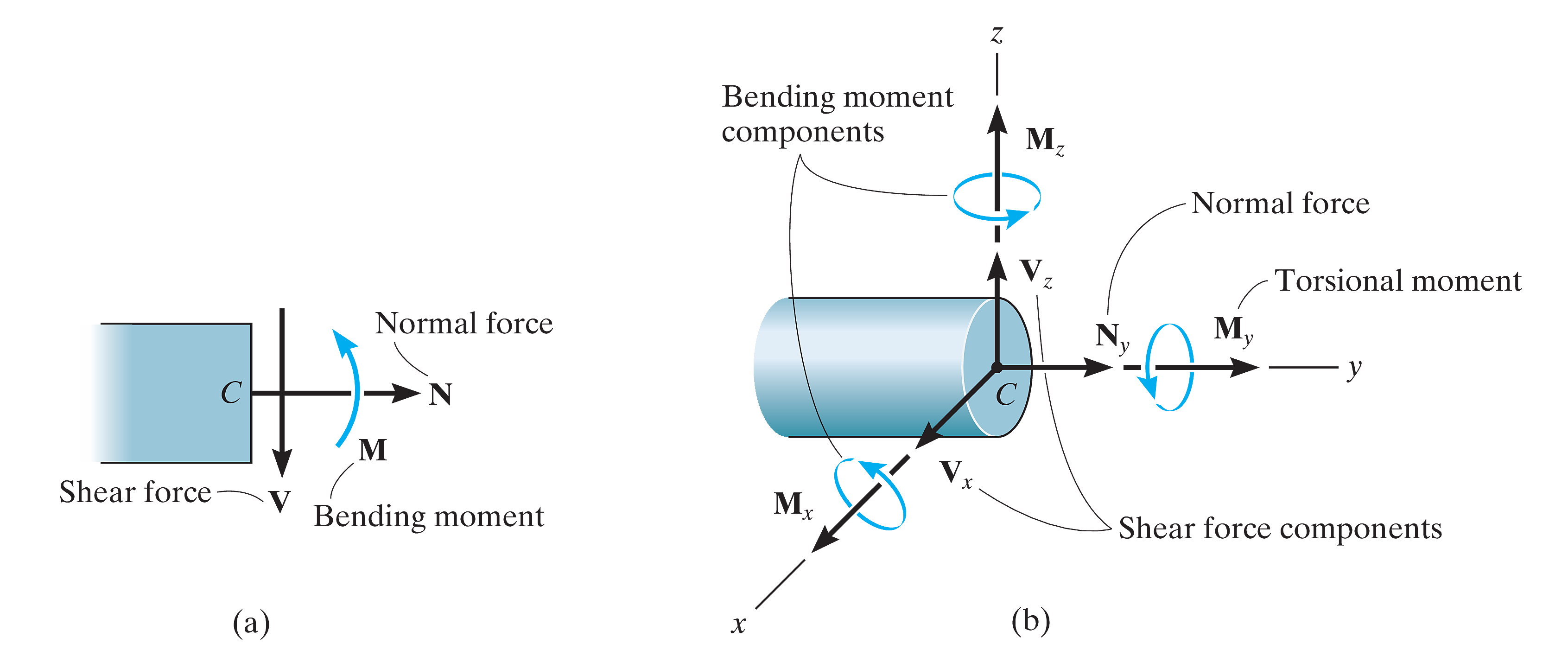
符号约定
轴向力受拉为正;剪切力顺时针旋转为正;弯矩向上为正。(如图)
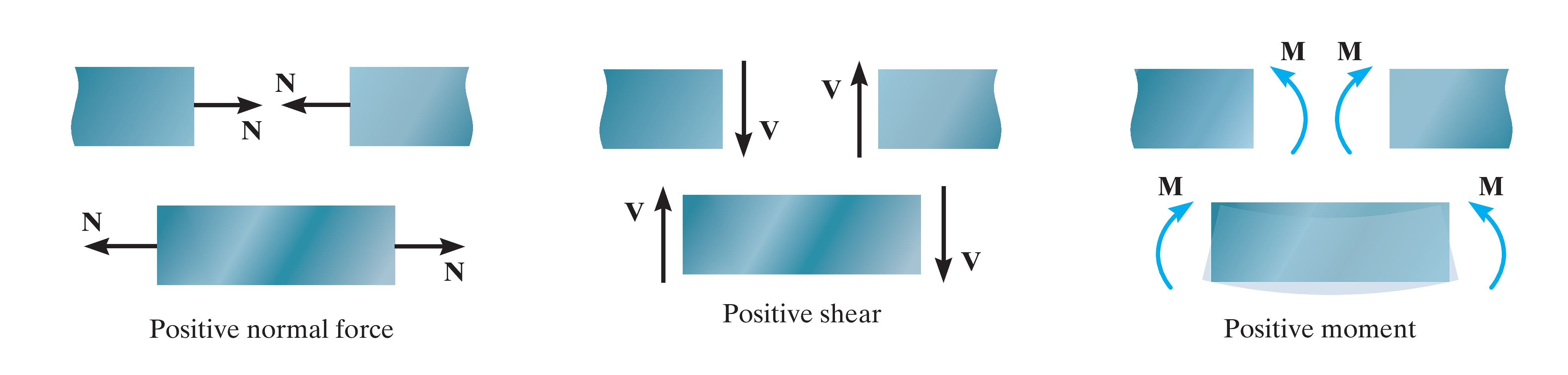
剪力方程、弯矩方程、剪力图、弯矩图
Shear and Moment Equations and Diagrams
不考虑 normal force 的理由: The internal normal force is not considered for two reasons. In most cases, the loads applied to a beam act perpendicular to the beam's axis and hence produce only an internal shear force and bending moment. And for design purposes, the beam's resistance to shear, and particularly to bending, is more important than its ability to resist a normal force.
学习资源
非常好的讲解剪力图、弯矩图的文章 The Efficient Engineer 和视频 The Efficient Engineer。
载荷、剪力与弯矩之间的关系
In the following discussion, the distributed load will be considered positive when this load acts upward as shown.
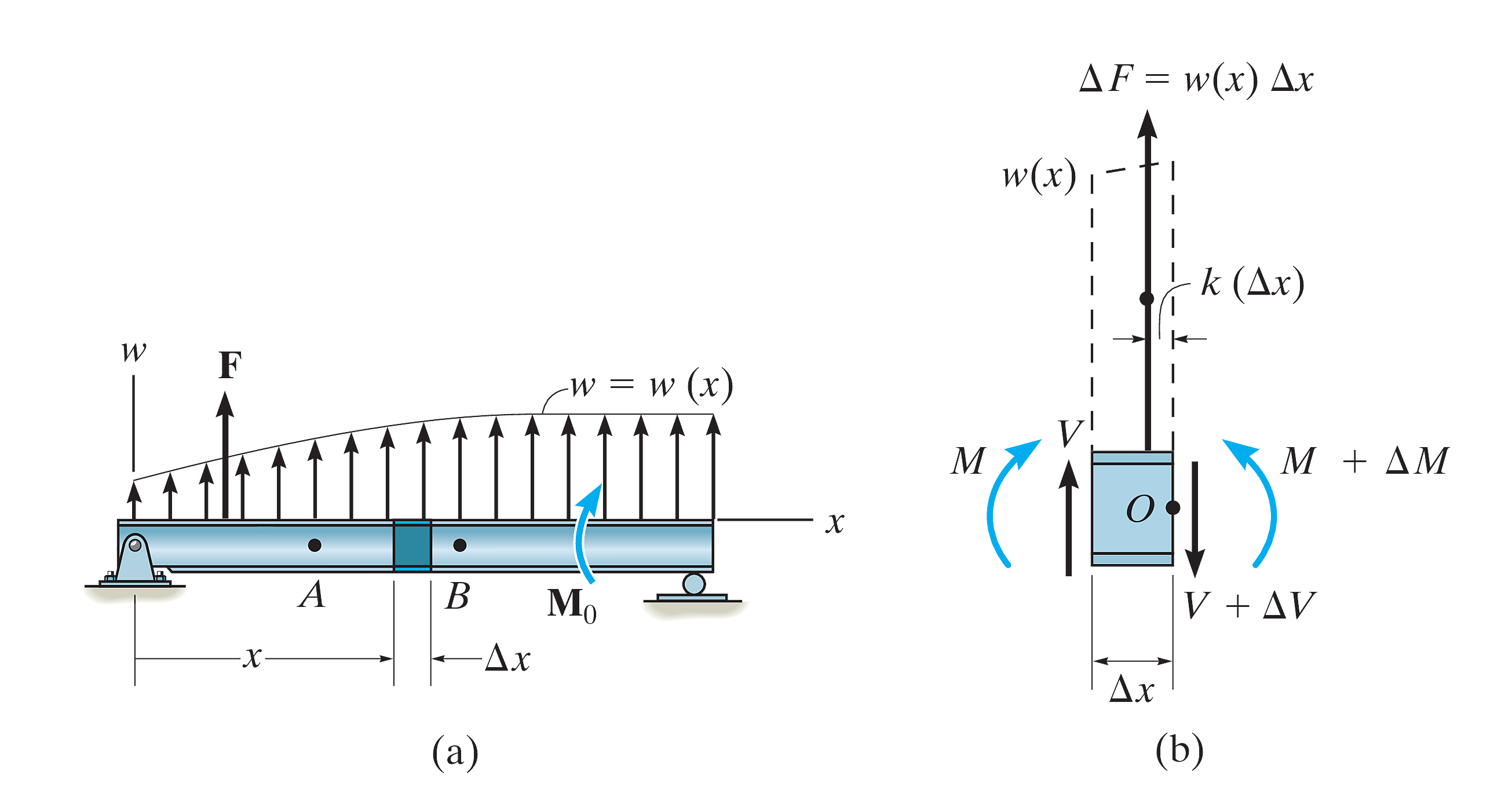
These equations do not apply at points where a concentrated force or couple moment act since these two special cases create discontinuities in the shear and moment diagrams.
缆绳
Cables
缆绳模型
核心假设:
完全柔性 (Perfectly Flexible): 这是最重要的假设。这个假设认为缆绳是完全柔软的,它不能承受任何弯矩 (bending moment,
) 或剪力 (shear force, )。这意味着缆绳内部的力永远是张力 (tension, ),并且这个张力的方向总是沿着缆绳自身的切线方向。 不可伸长 (Inextensible): 假设缆绳的长度在受力后不会发生改变。这意味着缆绳不会被拉伸。因此,一旦施加载荷,缆绳的几何形状保持不变,缆绳或其一部分可以被视为刚体。
基于这两个假设,可以分析缆绳在不同载荷下的形状和张力。以下将讨论三种情况:
承受集中载荷
Cable Subjected to Concentrated Loads.
核心思想:
当缆绳承受的是集中载荷时(比如在几个特定点上挂重物),它的形状会发生显著变化:
形状是折线:缆绳不是平滑的曲线,而是由一系列直线段 (straight line segments) 组成。
为什么是直线:考虑任意两个集中载荷之间的那一段缆绳。因为这段缆绳中间没有受到任何外力,根据静力平衡,它两端受到的张力必须大小相等、方向相反、作用在同一直线上。要满足这些条件,这段缆绳自身的几何形状必须是直线。
张力变化:在每一个悬挂重物的节点上,缆绳的方向会发生改变,因此缆绳的张力大小也会发生改变。
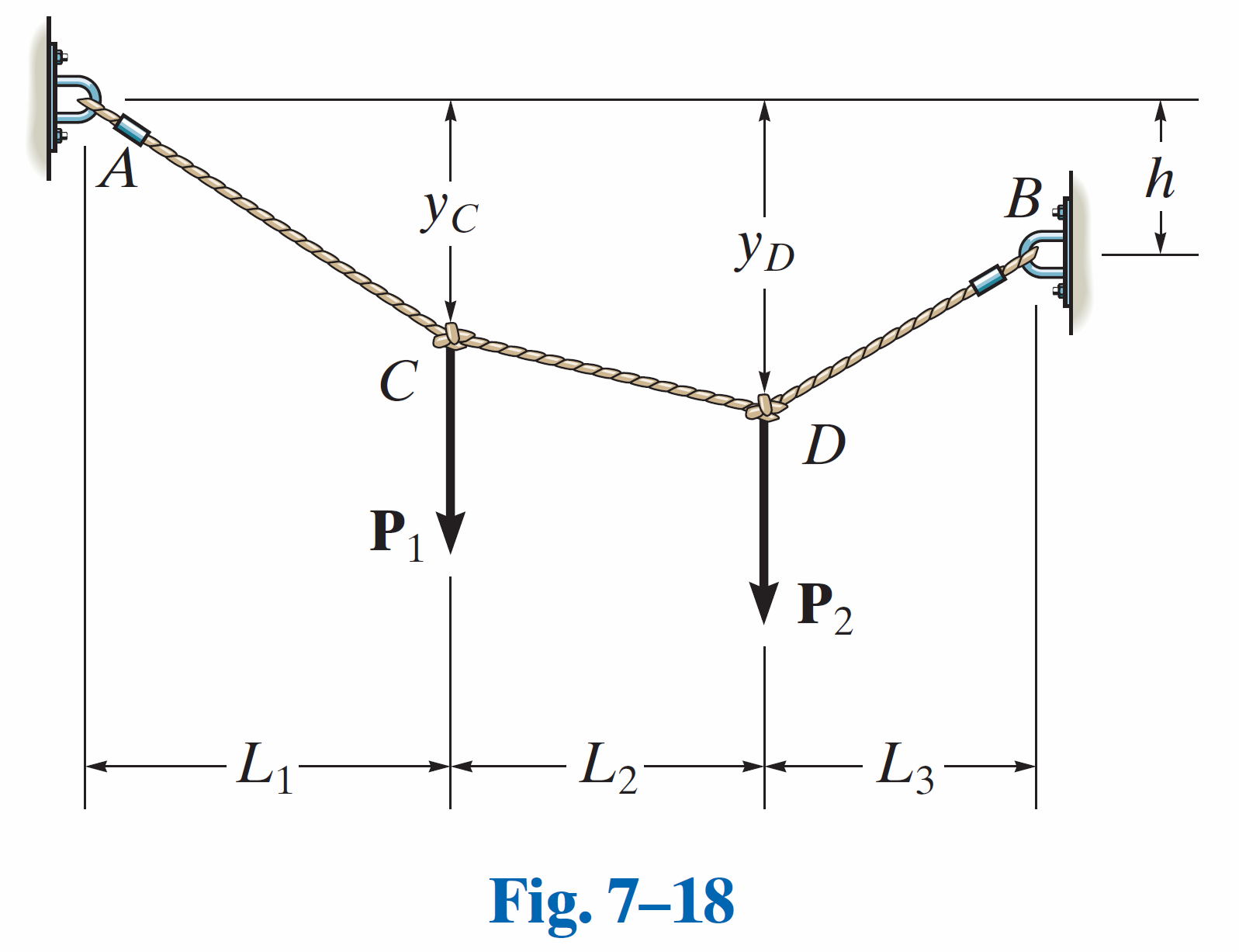
承受分布载荷
Cable Subjected to a Distributed Load.
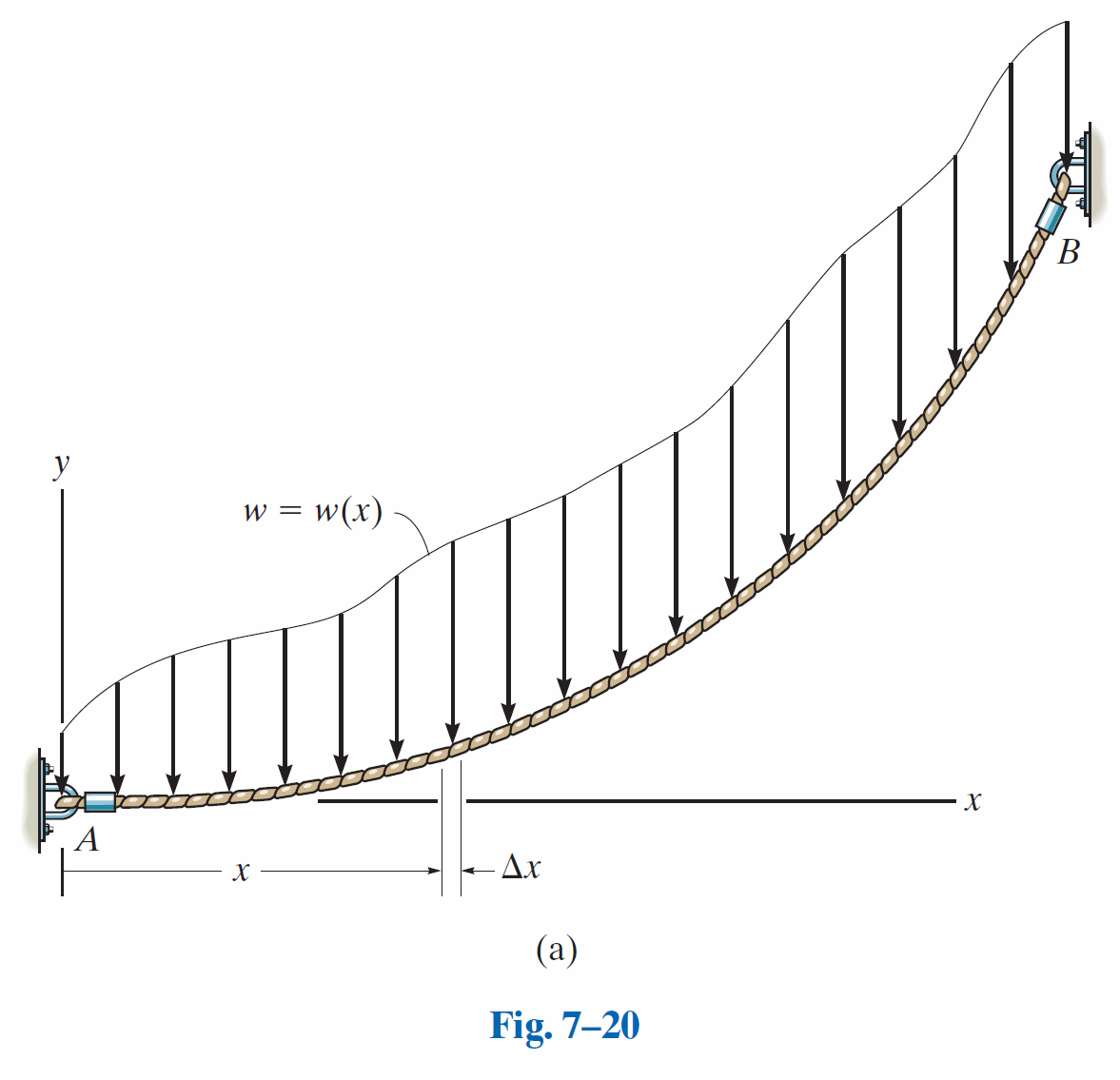
如图所示:
左侧的拉力
: 方向与缆绳在点 的切线方向相同,与水平方向的夹角为 。 右侧的拉力
: 方向与缆绳在点 的切线方向相同,与水平方向的夹角为 。 外部的分布载荷
: 方向通常是竖直向下(例如重力)。
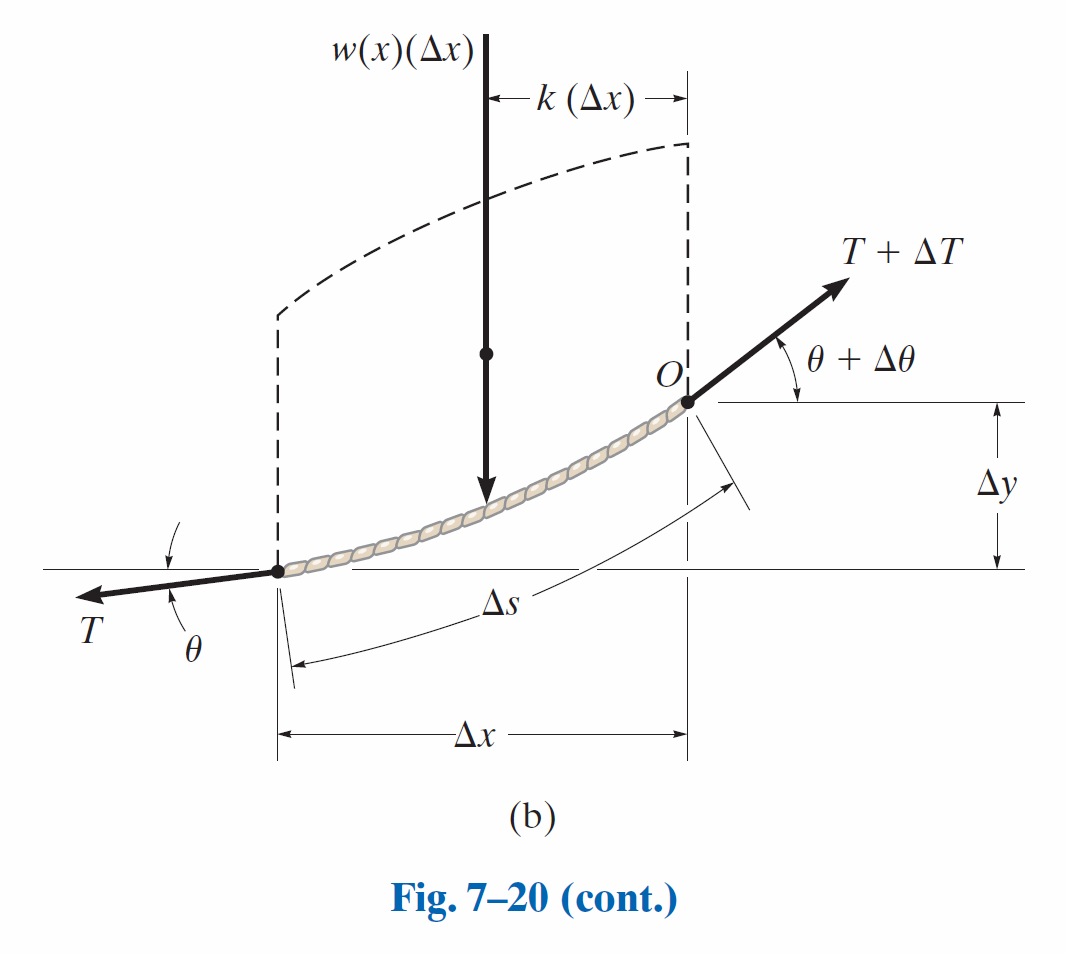
列出平衡方程组:
- 水平方向平衡 (
):
- 垂直方向平衡 (
):
- 点
处力矩平衡 ( ):
对上述三个平衡方程的两边同时除以
对等式
where
对等式
等式
对等式
这个方程用于确定缆绳的曲线,即
承受自身重量
Cable Subjected to Its Own Weight.
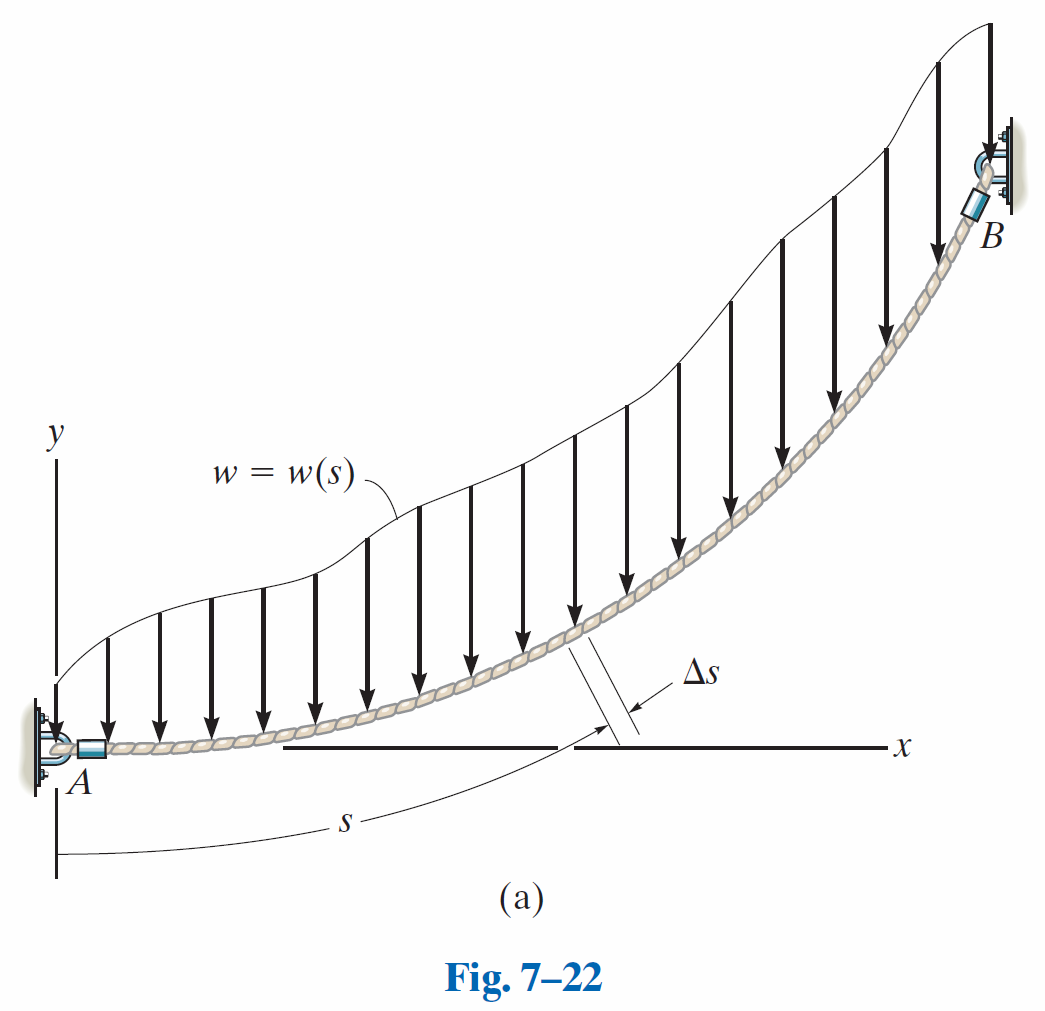
与情况“承受分布载荷”不同的是,
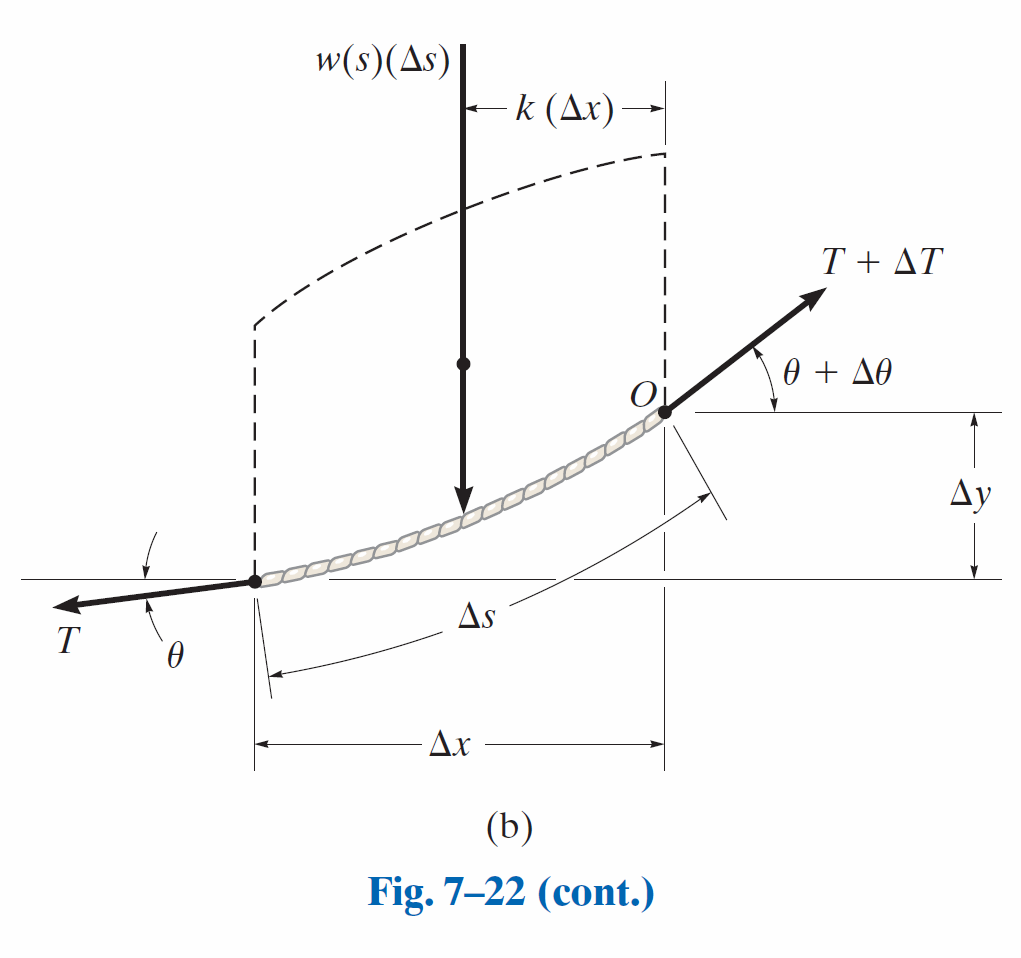
为了能对等式
于是:
进一步:
对上式进行分离变量并积分,可得:
两个积分常数,假设为
悬链线
Catenary
核心假设:
荷载是缆绳的自重,且沿弧长均匀分布 (Load is uniform along the arc length)。
将一般缆绳问题特定为悬链线问题的核心假设。
这个假设意味着每单位长度的缆绳具有相同的重量。通常用常数
来表示这个值(单位:N/m)。 在数学上,这个假设可以表示为:
。
推导步骤:
第1步:应用悬链线的荷载假设
根据悬链线的基本假设,
第2步:将结果代回“母公式”
第3步:求解积分
这是一个可以求解的积分。为了使形式更清晰,进行变量代换。
令
对
将这些代入积分表达式中:
这是一个标准的积分形式,通过查询积分表可知其结果是反双曲正弦函数
所以有:
第4步:使用边界条件确定积分常数
正如在开头所约定的,弧长
将边界条件
因为
这样,积分常数就被消掉,得到
第5步:引入常数 c 并反解出 s=f(x)
为了简化表达式,引入常数
通过以下计算过程可得
上式被称为悬链线的弧长表达式。
第6步:解出悬链线方程式
为了得到悬链线方程式,需要用到以下等式(均可在之前的内容中得到):
把等式 2. 代入到等式 1. 可得:
对上式积分,可得:
为了让公式简洁,悬链线的通常建系方法是:令缆绳的最低点对应坐标
最终的结果——悬链线方程式:
示例
完成每节后面的 FUNDAMENTAL PROBLEMS 以作加深理解的训练。
F7-1. ~ F7-6. 题目

这一部分的受力分析均用 OneNote 鼠标绘制。
F7-1.
受力分析
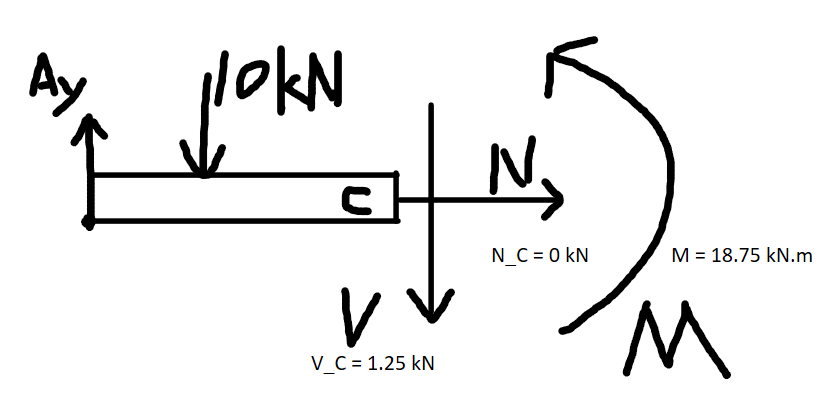
Python 解题
import sympy as sp
# 分析左半
# 第一步,已知 Sigma M_B = 0,求 A_y
A_y = sp.symbols('A_y', real=True)
eq = sp.Eq(- 6.0 * A_y + 4.5 * 10e3 + 1.5 * 15e3, 0)
sol = sp.solve(eq, A_y, dict=True)
A_y = sol[0][A_y]
# 第二步,已知 Sigma M_C = 0,求 C 点处的自由力矩
M = sp.symbols('M', real=True)
eq = sp.Eq(- 3.0 * A_y + 1.5 * 10e3 + M, 0)
sol = sp.solve(eq, M, dict=True)
M = sol[0][M]
# 第三步,已知 Sigma F_y = 0,求 V_C
V_C = sp.symbols('V_C', real=True)
eq = sp.Eq(- V_C - 10e3 + A_y, 0)
sol = sp.solve(eq, V_C, dict=True)
V_C = sol[0][V_C]
V_C
# N_C = 0
N_C = 0
print(f"N_C = {N_C/1e3:.2f} kN")
print(f"V_C = {V_C/1e3:.2f} kN")
print(f"M_C = {M/1e3:.2f} kN.m")输出:
N_C = 0.00 kN
V_C = 1.25 kN
M_C = 18.75 kN.mF7-2.
受力分析
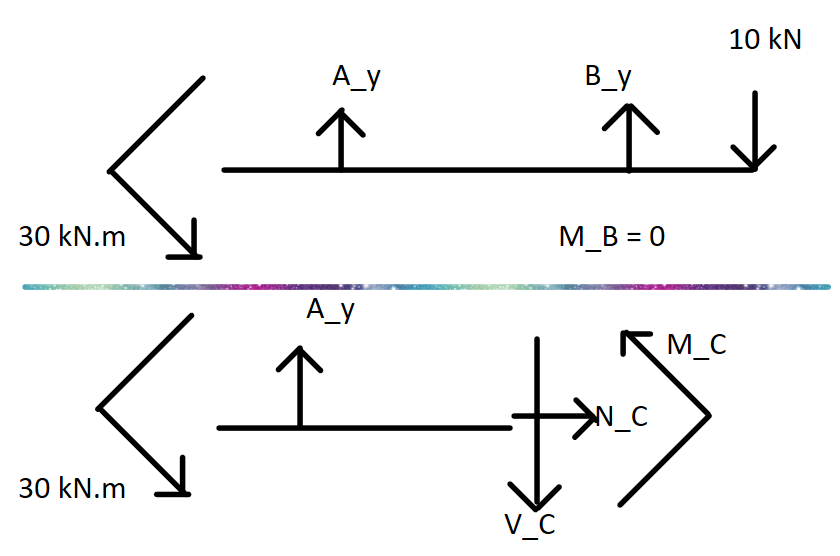
Python 解题
import sympy as sp
# 利用 M_B = 0,求 A_y
# 规定力矩的正方向为逆时针
A_y = sp.symbols('A_y', real=True)
eq = sp.Eq(30e3 - 3.0 * A_y - 1.5 * 10e3, 0)
sol = sp.solve(eq, A_y, dict=True)
A_y = sol[0][A_y]
# 利用 Sigma F_y = 0,求 V_C
V_C = sp.symbols('V_C', real=True)
eq = sp.Eq(A_y - V_C, 0)
sol = sp.solve(eq, V_C, dict=True)
V_C = sol[0][V_C]
# 求 M_C
M_C = sp.symbols('M_C', real=True)
eq = sp.Eq(30e3 - 1.5 * A_y + M_C, 0)
sol = sp.solve(eq, M_C, dict=True)
M_C = sol[0][M_C]
# N_C = 0
N_C = 0
print(f"N_C = {N_C/1e3:.2f} kN")
print(f"V_C = {V_C/1e3:.2f} kN")
print(f"M_C = {M_C/1e3:.2f} kN.m")输出:
N_C = 0.00 kN
V_C = 5.00 kN
M_C = -22.50 kN.mF7-3.
受力分析
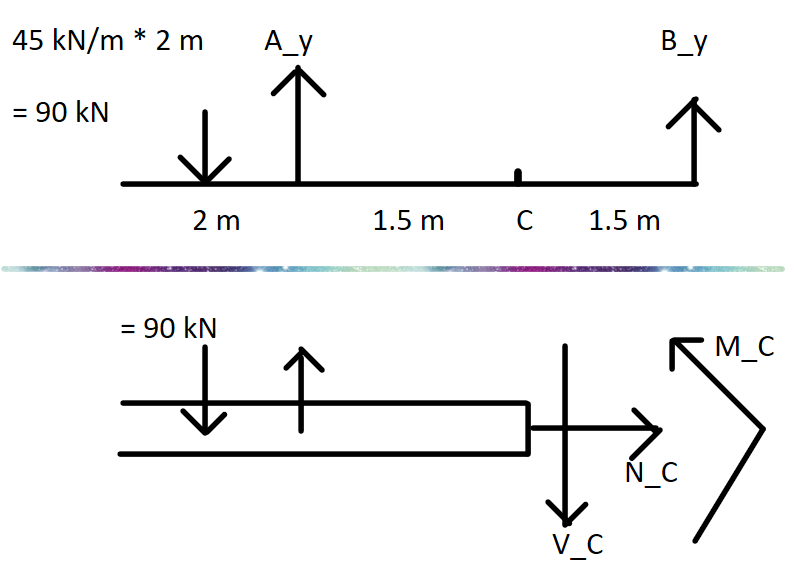
Python 解题
import sympy as sp
# 求 A_y
A_y = sp.symbols('A_y', real=True)
eq = sp.Eq(4 * 90e3 - 3.0 * A_y, 0)
sol = sp.solve(eq, A_y, dict=True)
A_y = sol[0][A_y]
# 求 V_C
V_C = sp.symbols('V_C', real=True)
eq = sp.Eq(- 90e3 + A_y - V_C, 0)
sol = sp.solve(eq, V_C, dict=True)
V_C = sol[0][V_C]
# 求 M_C
M_C = sp.symbols('M_C', real=True)
eq = sp.Eq(2.5 * 90e3 - 1.5 * A_y + M_C, 0)
sol = sp.solve(eq, M_C, dict=True)
M_C = sol[0][M_C]
# N_C = 0
N_C = 0
print(f"N_C = {N_C/1e3:.2f} kN")
print(f"V_C = {V_C/1e3:.2f} kN")
print(f"M_C = {M_C/1e3:.2f} kN.m")输出:
N_C = 0.00 kN
V_C = 30.00 kN
M_C = -45.00 kN.mF7-4.
受力分析
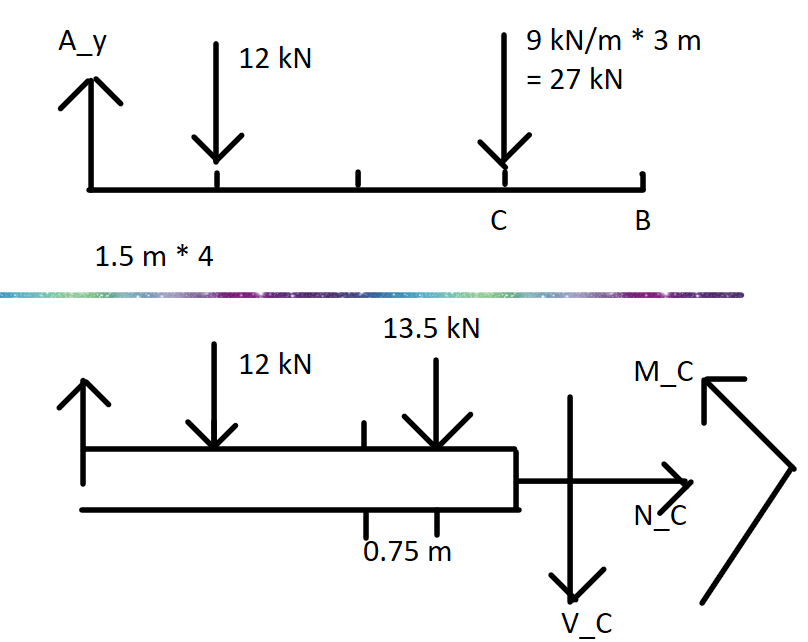
Python 解题
# F7-4.
import sympy as sp
# 求 A_y
A_y = sp.symbols('A_y', real=True)
eq = sp.Eq(- 6.0 * A_y + 4.5 * 12e3 + 1.5 * 27e3, 0)
sol = sp.solve(eq, A_y, dict=True)
A_y = sol[0][A_y]
# 求 V_C
V_C = sp.symbols('V_C', real=True)
eq = sp.Eq(A_y - 12e3 - 13.5e3 - V_C, 0)
sol = sp.solve(eq, V_C, dict=True)
V_C = sol[0][V_C]
# 求 M_C
M_C = sp.symbols('M_C', real=True)
eq = sp.Eq(- 4.5 * A_y + 3.0 * 12e3 + 0.75 * 13.5e3 + M_C, 0)
sol = sp.solve(eq, M_C, dict=True)
M_C = sol[0][M_C]
# N_C = 0
N_C = 0
print(f"N_C = {N_C/1e3:.2f} kN")
print(f"V_C = {V_C/1e3:.2f} kN")
print(f"M_C = {M_C/1e3:.2f} kN.m")输出:
N_C = 0.00 kN
V_C = -9.75 kN
M_C = 24.75 kN.mF7-5.
受力分析
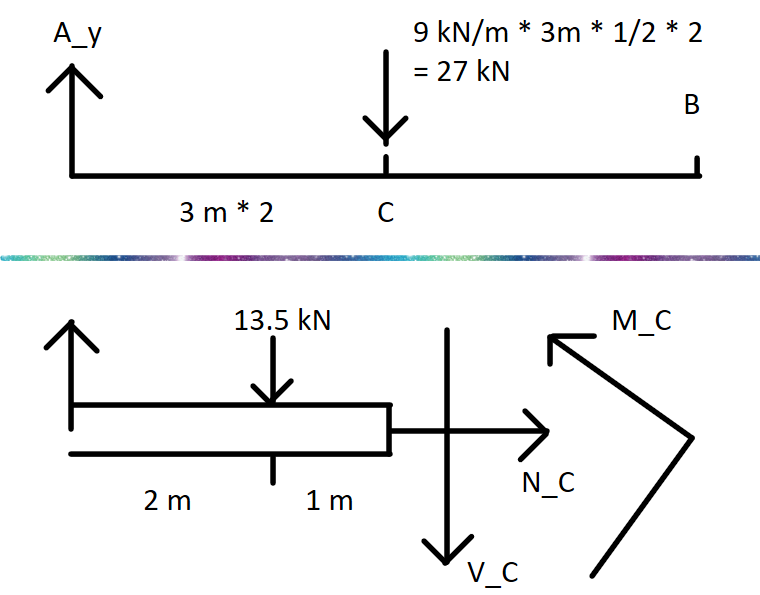
Python 解题
import sympy as sp
# 求 A_y
A_y = sp.symbols('A_y', real=True)
eq = sp.Eq(- 6.0 * A_y + 3.0 * 27e3, 0)
sol = sp.solve(eq, A_y, dict=True)
A_y = sol[0][A_y]
# 求 V_C
V_C = sp.symbols('V_C', real=True)
eq = sp.Eq(A_y - 13.5e3 - V_C, 0)
sol = sp.solve(eq, V_C, dict=True)
V_C = sol[0][V_C]
# 求 M_C
M_C = sp.symbols('M_C', real=True)
eq = sp.Eq(- 3.0 * A_y + 1.0 * 13.5e3 + M_C, 0)
sol = sp.solve(eq, M_C, dict=True)
M_C = sol[0][M_C]
# N_C = 0
N_C = 0
print(f"N_C = {N_C/1e3:.2f} kN")
print(f"V_C = {V_C/1e3:.2f} kN")
print(f"M_C = {M_C/1e3:.2f} kN.m")输出:
N_C = 0.00 kN
V_C = 0.00 kN
M_C = 27.00 kN.mF7-6.
受力分析
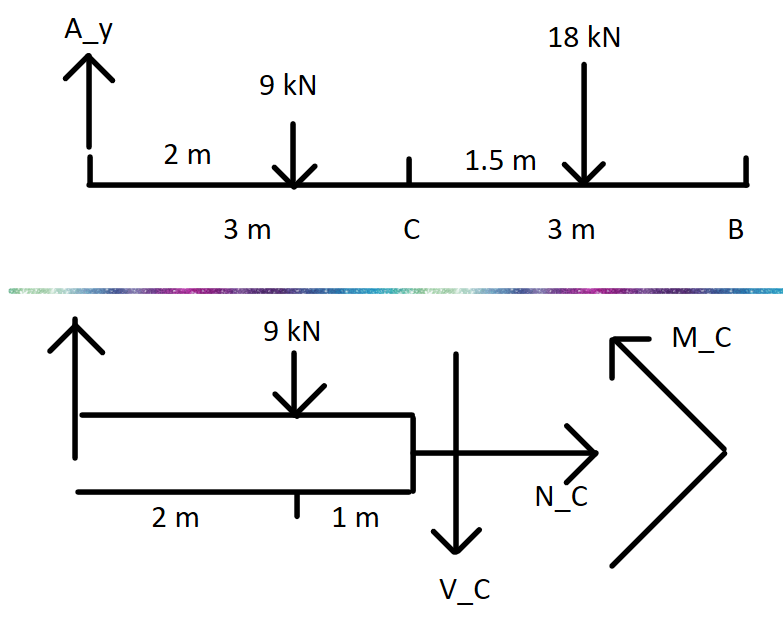
Python 解题
import sympy as sp
# 求 A_y
A_y = sp.symbols('A_y', real=True)
eq = sp.Eq(- 6.0 * A_y + 4.0 * 9e3 + 1.5 * 18e3, 0)
sol = sp.solve(eq, A_y, dict=True)
A_y = sol[0][A_y]
# 求 V_C
V_C = sp.symbols('V_C', real=True)
eq = sp.Eq(A_y - 9e3 - V_C, 0)
sol = sp.solve(eq, V_C, dict=True)
V_C = sol[0][V_C]
# 求 M_C
M_C = sp.symbols('M_C', real=True)
eq = sp.Eq(- 3.0 * A_y + 1.0 * 9e3 + M_C, 0)
sol = sp.solve(eq, M_C, dict=True)
M_C = sol[0][M_C]
# N_C = 0
N_C = 0
print(f"N_C = {N_C/1e3:.2f} kN")
print(f"V_C = {V_C/1e3:.2f} kN")
print(f"M_C = {M_C/1e3:.2f} kN.m")输出:
N_C = 0.00 kN
V_C = 1.50 kN
M_C = 22.50 kN.mF7-7. ~ F7-12. 题目

使用 latex 作图。
F7-7.
解题

F7-8.
解题

F7-9.
解题

F7-10.
解题

F7-11.
解题

F7-12.
解题

F7-13. ~ F7-18. 题目
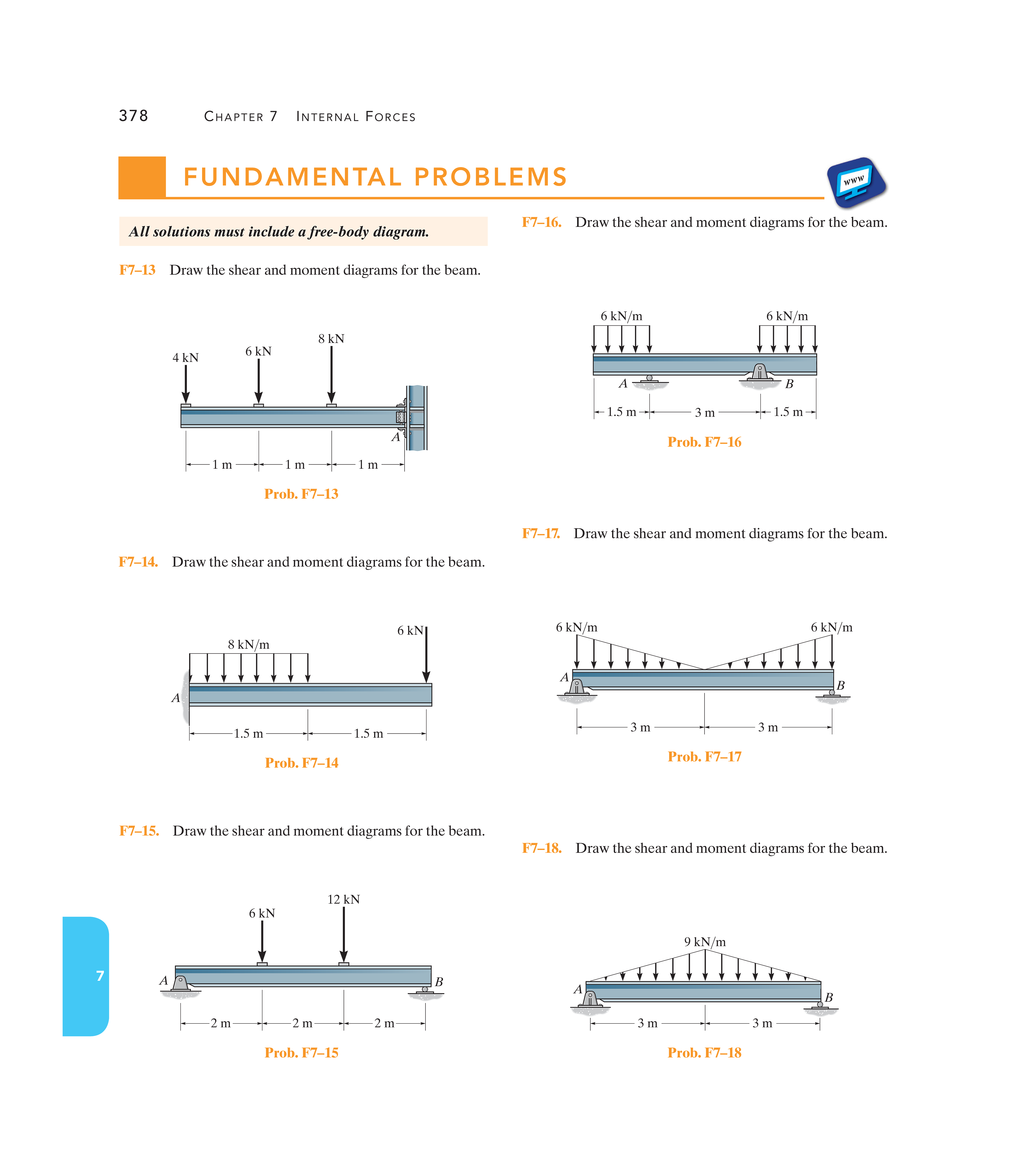
Latex 作图。
F7-13.
解题

F7-14.
解题

F7-15.
解题

F7-16.
解题

F7-17.
解题

F7-18.
解题

